2021-2022学年人教版八年级数学上册13.3 等腰三角形同步练习(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.3 等腰三角形同步练习(word版、含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 454.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 11:20:52 | ||
图片预览


文档简介
13.3 等腰三角形-—2021-2022学年八年级数学人教版
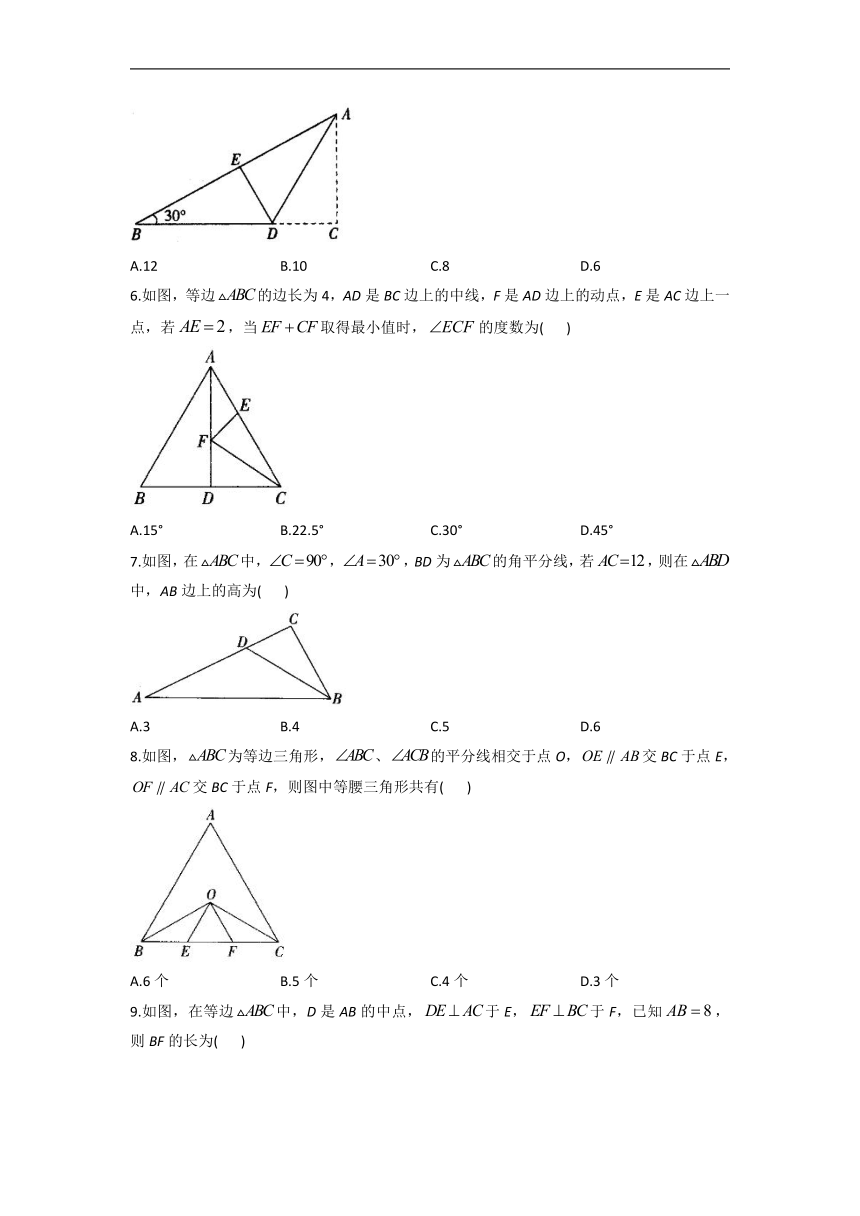
1.如图,AD是等腰三角形ABC的顶角平分线,,则CD等于( )
A.10 B.5 C.4 D.3
2.如图,是等边三角形,,,则的度数是( )
A.40° B.50° C.60° D.70°
3.下面给出几个三角形:
(1)有两个角为60°的三角形;
(2)一边上的高也是这边上的中线的三角形;
(3)有一个角为60°的等腰三角形,
其中等边三角形的个数是( )
A.0 B.3 C.2 D.1
4.如图,等腰的周长为21,底边,AB的垂直平分线DE交AB于点D,交AC于点E,则的周长为( )
A.13 B.14 C.15 D.16
5.如图,折叠直角三角形纸片,使直角顶点C落在AB边上的点E处,已知,,则DE的长是( )
A.12 B.10 C.8 D.6
6.如图,等边的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若,当取得最小值时,的度数为( )
A.15° B.22.5° C.30° D.45°
7.如图,在中,,,BD为的角平分线,若,则在中,AB边上的高为( )
A.3 B.4 C.5 D.6
8.如图,为等边三角形,、的平分线相交于点O,交BC于点E,交BC于点F,则图中等腰三角形共有( )
A.6个 B.5个 C.4个 D.3个
9.如图,在等边中,D是AB的中点,于E,于F,已知,则BF的长为( )
A.3 B.4 C.5 D.6
10.如图,在中,与的平分线交于点I,过点I作交BA于点D,交AC于点E,且,,,则下列说法错误的是( )
A.和是等腰三角形 B.
C.的周长是8 D.
11.等边三角形是一个轴对称图形,它有_____________条对称轴.
12.将一副三角尺按图所示方式叠放在一起,若cm,则阴影部分的面积是_________.
13.“三等分角”大约是在公元前5世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,,点D、E可在槽中滑动,为的三等分角.若,则的度数是___________.
14.如图,CE、CF分别平分和,,,则____________.
15.定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”.
(1)如图①,中,,,求证:是倍角三角形;
(2)如图②,的外角平分线AD与CB的延长线相交于点D,延长CA到点E,使得,若,请你找出图中的倍角三角形,并进行证明.
答案以及解析
1.答案:B
解析:AD是等腰三角形ABC的顶角平分线,,
.故选B.
2.答案:C
解析:是等边三角形,,,在和中,,,,故选C.
3.答案:C
解析:易知(1)有两个角为60°的三角形的三个内角都是60°,(3)有一个角是60°的等腰三角形是等边三角形,所以(1)(3)为等边三角形,故等边三角形的个数是2.
4.答案:A
解析:为等腰三角形,,,,,直线DE是线段AB的垂直平分线,,故,的周长.故选A.
5.答案:C
解析:与关于AD对称,,,,.,.,,.
6.答案:C
解析:如图,过E作,交AD于点N,交AB于点M.,,,,, AD是BC边上的中线,是等边三角形,,,,, E和M关于AD对称,连接CM,交AD于点F,连接EF,此时的值最小,是等边三角形,,,故选C.
7.答案:B
解析:如图,过D作于E,
,,
,
BD平分,
,
,,
,,
,,BD平分,
,故选B.
8.答案:B
解析:为等边三角形,为等腰三角形,.BO、CO分别平分、,,,,为等腰三角形.,,为等腰三角形.同理,为等腰三角形.,,,,,为等腰三角形.题图中共有5个等腰三角形.故选B.
9.答案:C
解析:在等边中,D是AB的中点,,,,,,,,,,,,,故选C.
10.答案:B
解析: BI平分,,,,,.同理,.和是等腰三角形.的周长.,,,,故选项A,C,D说法正确,故选B.
11.答案:3
解析:等边三角形各边高线所在直线都是其对称轴,共有3条对称轴.
12.答案:
解析:在中,,cm,,cm,是等腰直角三角形,,,cm,.
13.答案:80°
解析:,,,,,,,,故答案为80°.
14.答案:5
解析: CE平分,.CF平分,.,,.,.,(等角对等边)..
15.答案:(1)证明:,,
,,
,
,即是倍角三角形.
(2)是倍角三角形.
证明: AD平分,,
,,
,
,,
又,
,即.
.
.
是倍角三角形.
1.如图,AD是等腰三角形ABC的顶角平分线,,则CD等于( )
A.10 B.5 C.4 D.3
2.如图,是等边三角形,,,则的度数是( )
A.40° B.50° C.60° D.70°
3.下面给出几个三角形:
(1)有两个角为60°的三角形;
(2)一边上的高也是这边上的中线的三角形;
(3)有一个角为60°的等腰三角形,
其中等边三角形的个数是( )
A.0 B.3 C.2 D.1
4.如图,等腰的周长为21,底边,AB的垂直平分线DE交AB于点D,交AC于点E,则的周长为( )
A.13 B.14 C.15 D.16
5.如图,折叠直角三角形纸片,使直角顶点C落在AB边上的点E处,已知,,则DE的长是( )
A.12 B.10 C.8 D.6
6.如图,等边的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若,当取得最小值时,的度数为( )
A.15° B.22.5° C.30° D.45°
7.如图,在中,,,BD为的角平分线,若,则在中,AB边上的高为( )
A.3 B.4 C.5 D.6
8.如图,为等边三角形,、的平分线相交于点O,交BC于点E,交BC于点F,则图中等腰三角形共有( )
A.6个 B.5个 C.4个 D.3个
9.如图,在等边中,D是AB的中点,于E,于F,已知,则BF的长为( )
A.3 B.4 C.5 D.6
10.如图,在中,与的平分线交于点I,过点I作交BA于点D,交AC于点E,且,,,则下列说法错误的是( )
A.和是等腰三角形 B.
C.的周长是8 D.
11.等边三角形是一个轴对称图形,它有_____________条对称轴.
12.将一副三角尺按图所示方式叠放在一起,若cm,则阴影部分的面积是_________.
13.“三等分角”大约是在公元前5世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,,点D、E可在槽中滑动,为的三等分角.若,则的度数是___________.
14.如图,CE、CF分别平分和,,,则____________.
15.定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”.
(1)如图①,中,,,求证:是倍角三角形;
(2)如图②,的外角平分线AD与CB的延长线相交于点D,延长CA到点E,使得,若,请你找出图中的倍角三角形,并进行证明.
答案以及解析
1.答案:B
解析:AD是等腰三角形ABC的顶角平分线,,
.故选B.
2.答案:C
解析:是等边三角形,,,在和中,,,,故选C.
3.答案:C
解析:易知(1)有两个角为60°的三角形的三个内角都是60°,(3)有一个角是60°的等腰三角形是等边三角形,所以(1)(3)为等边三角形,故等边三角形的个数是2.
4.答案:A
解析:为等腰三角形,,,,,直线DE是线段AB的垂直平分线,,故,的周长.故选A.
5.答案:C
解析:与关于AD对称,,,,.,.,,.
6.答案:C
解析:如图,过E作,交AD于点N,交AB于点M.,,,,, AD是BC边上的中线,是等边三角形,,,,, E和M关于AD对称,连接CM,交AD于点F,连接EF,此时的值最小,是等边三角形,,,故选C.
7.答案:B
解析:如图,过D作于E,
,,
,
BD平分,
,
,,
,,
,,BD平分,
,故选B.
8.答案:B
解析:为等边三角形,为等腰三角形,.BO、CO分别平分、,,,,为等腰三角形.,,为等腰三角形.同理,为等腰三角形.,,,,,为等腰三角形.题图中共有5个等腰三角形.故选B.
9.答案:C
解析:在等边中,D是AB的中点,,,,,,,,,,,,,故选C.
10.答案:B
解析: BI平分,,,,,.同理,.和是等腰三角形.的周长.,,,,故选项A,C,D说法正确,故选B.
11.答案:3
解析:等边三角形各边高线所在直线都是其对称轴,共有3条对称轴.
12.答案:
解析:在中,,cm,,cm,是等腰直角三角形,,,cm,.
13.答案:80°
解析:,,,,,,,,故答案为80°.
14.答案:5
解析: CE平分,.CF平分,.,,.,.,(等角对等边)..
15.答案:(1)证明:,,
,,
,
,即是倍角三角形.
(2)是倍角三角形.
证明: AD平分,,
,,
,
,,
又,
,即.
.
.
是倍角三角形.
