陕西省咸阳市三原县城关北城高级中学2021-2022学年高一上学期12月月考数学试题(Word版含答案)
文档属性
| 名称 | 陕西省咸阳市三原县城关北城高级中学2021-2022学年高一上学期12月月考数学试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 14:51:43 | ||
图片预览



文档简介
三原县城关北城高级中学2021-2022学年高一上学期12月月考
数学试卷
一、单选题
1.函数 的最小值是( )
A. 4 B. C. D.
2.已知圆心角为 的扇形内部有一个圆C与扇形的半径及圆弧均相切,当圆C面积为 时,该扇形的面积为( )
A. B. C. D.
3.在平面直角坐标系中,过点(2,1)且倾斜角为 的直线不经过 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.设函数 , 则 的值域是( )
A. B.
C. D.
5.已知 ,则( )
A. a6.已知函数 ,用二分法求 的零点时,则其中一个零点的初始区间可以为( )
A. B. C. D.
7.已知 是定义在R上的偶函数,当 时, ,则 ( )
A. 11 B. 6 C. -6 D. -11
8.三个数175,100,75的最大公约数是( )
A. 5 B. 25 C. 75 D. 50
9.祖暅(公元5-6世纪,祖冲之之子),是我国齐梁时代的数学家,他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为 ,高皆为 的椭半球体和已被挖去了圆锥体的圆柱体放置于同一平面 上,以平行于平面 的平面于距平面 任意高 处可横截得到 及 两截面,可以证明 总成立.据此,短轴 长为 ,长半轴 为 的椭半球体的体积是( )
A.
B.
C.
D.
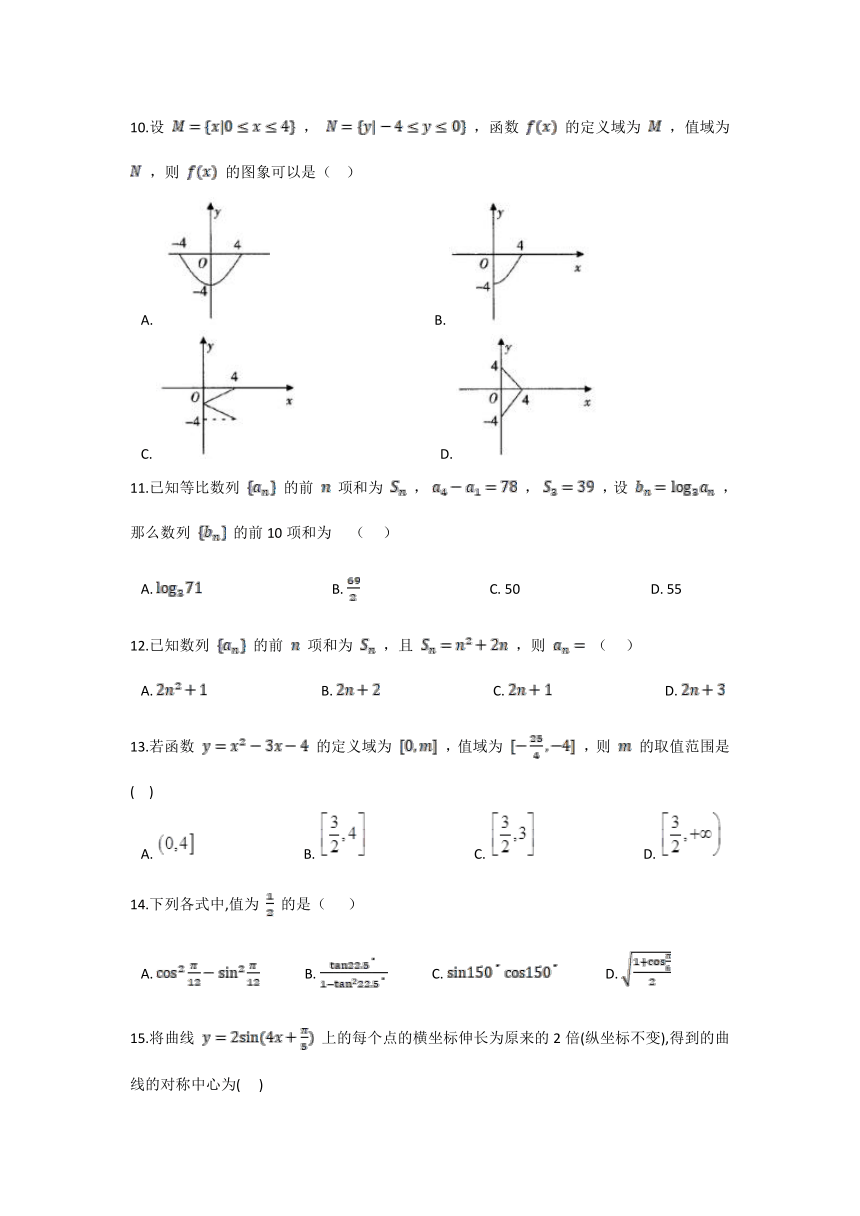
10.设 , ,函数 的定义域为 ,值域为 ,则 的图象可以是( )
A. B.
C. D.
11.已知等比数列 的前 项和为 , , ,设 ,那么数列 的前10项和为 ( )
A. B. C. 50 D. 55
12.已知数列 的前 项和为 ,且 ,则 ( )
A. B. C. D.
13.若函数 的定义域为 ,值域为 ,则 的取值范围是( )
A. B. C. D.
14.下列各式中,值为 的是( )
A. B. C. D.
15.将曲线 上的每个点的横坐标伸长为原来的2倍(纵坐标不变),得到的曲线的对称中心为( )
A. B.
C. D.
16.已知 , , ,则 的大小关系是( )
A. B.
C. D.
17.函数 (e≈2.718281828459)的部分图象大致是( )
A. B.
C. D.
18.已知 ,那么 的值为( )
A. B. C. D.
19.已知数列 为等差数列,首项 ,若 ,则使得 的n的最大值为( )
A. 2007 B. 2008 C. 2009 D. 2010
20.为加强环境保护,治理空气污染,某环保部门对辖区内一工厂产生的废气进行了监测,发现该厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量 与时间 的关系为 .如果在前5个小时消除了 的污染物,那么该厂产生的废气过滤10个小时后,消除污染物的百分比为( )
A. 10% B. 19% C. 20% D. 80%
二、解答题
21.我国所需的高端芯片很大程度依赖于国外进口,“缺芯之痛”关乎产业安全、国家经济安全.如今,我国科技企业正在芯片自主研发之路中不断崛起.根据市场调查某手机品牌公司生产某款手机的年固定成本为40万美元,每生产1万部还需另投入16万美元.设该公司一年内共生产该款手机 万部并全部销售完,每万部的销售收入为 万美元,且 当该公司一年内共生产该款手机2万部并全部销售完时,年利润为704万美元.
(1)写出年利润 (万美元)关于年产量 (万部)的函数解析式:
(2)当年产量为多少万部时,公司在该款手机的生产中所获得的利润最大 并求出最大利润.
22.如图所示,某海岛上一观察哨 上午 时测得一轮船在海岛北偏东 的 处, 时 分测得船在海岛北偏西 的 处, 时 分轮船到达位于海岛正西方且距海岛 的 港口,如果轮船始终匀速直线前进,求船速多少.
23. 是偶函数,
(1)求 的值;
(2)当 时,设 ,若函数 与 的图象有且只有一个公共点,求实数 的取值范围.
24.已知向量 ,其中 .
(1)若的 ,求 的值;
(2)若 与 垂直,求实数 的取值范围.
答案解析部分
一、单选题
1.【答案】 D
2.【答案】 D
3.【答案】 C
4.【答案】 D
5.【答案】 A
6.【答案】 C
7.【答案】 A
8.【答案】 B
9.【答案】 A
10.【答案】 B
11.【答案】 D
12.【答案】 C
13.【答案】 C
14.【答案】 B
15.【答案】 A
16.【答案】 B
17.【答案】 B
18.【答案】 A
19.【答案】 B
20.【答案】 B
二、解答题
21.【答案】 (1)解:因为生产该款手机2万部并全部销售完时,年利润为704万美元.
所以 ,
解得 ,
当 时, ,
当 时, .
所以
(2)解:①当 时, ,所以 ;
②当 时, ,由于 ,
当且仅当 ,即 时,取等号,所以此时 的最大值为5760.
综合①②知,当 , 取得最大值为6104万美元.
22.【答案】 解:轮船从C到B用时80分钟,从B到E用时20分钟,
而船始终匀速前进,由此可见:BC=4EB,设EB= ,则
则BC=4 ,由已知得
在△AEC中,由正弦定理得:
在△ABC中,由正弦定理得:
在△ABE中,由余弦定理得:
所以船速 答:该船的速度为 km/h
23.【答案】 (1)因为 为偶函数.
所以 ,即 .
.
.
(2)由已知,方程 有且只有一个解.
有且只有一个解,且满足 .
整理得 .
令 ,则方程 在 有且只有一个实根.
当 时, ,不满足题意,舍去.
当 时,设方程对应的二次函数为 .
抛物线开口向上,对称轴 ,且 .
只需 ,则方程只有一个大于2 的根.
而 ,即 时满足题意.
当 时,抛物线开口向下,对称轴 ,且 .
此时方程无大于2 的实根.
综上 .
24.【答案】 (1)解:因为 ,
即 ,
所以 ,
所以 ,即 或 .
因为 ,所以 ,即 ;
(2)解:因为 与 垂直,
,
,
所以 ,因为 ,
所以 ,
即 .
数学试卷
一、单选题
1.函数 的最小值是( )
A. 4 B. C. D.
2.已知圆心角为 的扇形内部有一个圆C与扇形的半径及圆弧均相切,当圆C面积为 时,该扇形的面积为( )
A. B. C. D.
3.在平面直角坐标系中,过点(2,1)且倾斜角为 的直线不经过 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.设函数 , 则 的值域是( )
A. B.
C. D.
5.已知 ,则( )
A. a
A. B. C. D.
7.已知 是定义在R上的偶函数,当 时, ,则 ( )
A. 11 B. 6 C. -6 D. -11
8.三个数175,100,75的最大公约数是( )
A. 5 B. 25 C. 75 D. 50
9.祖暅(公元5-6世纪,祖冲之之子),是我国齐梁时代的数学家,他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为 ,高皆为 的椭半球体和已被挖去了圆锥体的圆柱体放置于同一平面 上,以平行于平面 的平面于距平面 任意高 处可横截得到 及 两截面,可以证明 总成立.据此,短轴 长为 ,长半轴 为 的椭半球体的体积是( )
A.
B.
C.
D.
10.设 , ,函数 的定义域为 ,值域为 ,则 的图象可以是( )
A. B.
C. D.
11.已知等比数列 的前 项和为 , , ,设 ,那么数列 的前10项和为 ( )
A. B. C. 50 D. 55
12.已知数列 的前 项和为 ,且 ,则 ( )
A. B. C. D.
13.若函数 的定义域为 ,值域为 ,则 的取值范围是( )
A. B. C. D.
14.下列各式中,值为 的是( )
A. B. C. D.
15.将曲线 上的每个点的横坐标伸长为原来的2倍(纵坐标不变),得到的曲线的对称中心为( )
A. B.
C. D.
16.已知 , , ,则 的大小关系是( )
A. B.
C. D.
17.函数 (e≈2.718281828459)的部分图象大致是( )
A. B.
C. D.
18.已知 ,那么 的值为( )
A. B. C. D.
19.已知数列 为等差数列,首项 ,若 ,则使得 的n的最大值为( )
A. 2007 B. 2008 C. 2009 D. 2010
20.为加强环境保护,治理空气污染,某环保部门对辖区内一工厂产生的废气进行了监测,发现该厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量 与时间 的关系为 .如果在前5个小时消除了 的污染物,那么该厂产生的废气过滤10个小时后,消除污染物的百分比为( )
A. 10% B. 19% C. 20% D. 80%
二、解答题
21.我国所需的高端芯片很大程度依赖于国外进口,“缺芯之痛”关乎产业安全、国家经济安全.如今,我国科技企业正在芯片自主研发之路中不断崛起.根据市场调查某手机品牌公司生产某款手机的年固定成本为40万美元,每生产1万部还需另投入16万美元.设该公司一年内共生产该款手机 万部并全部销售完,每万部的销售收入为 万美元,且 当该公司一年内共生产该款手机2万部并全部销售完时,年利润为704万美元.
(1)写出年利润 (万美元)关于年产量 (万部)的函数解析式:
(2)当年产量为多少万部时,公司在该款手机的生产中所获得的利润最大 并求出最大利润.
22.如图所示,某海岛上一观察哨 上午 时测得一轮船在海岛北偏东 的 处, 时 分测得船在海岛北偏西 的 处, 时 分轮船到达位于海岛正西方且距海岛 的 港口,如果轮船始终匀速直线前进,求船速多少.
23. 是偶函数,
(1)求 的值;
(2)当 时,设 ,若函数 与 的图象有且只有一个公共点,求实数 的取值范围.
24.已知向量 ,其中 .
(1)若的 ,求 的值;
(2)若 与 垂直,求实数 的取值范围.
答案解析部分
一、单选题
1.【答案】 D
2.【答案】 D
3.【答案】 C
4.【答案】 D
5.【答案】 A
6.【答案】 C
7.【答案】 A
8.【答案】 B
9.【答案】 A
10.【答案】 B
11.【答案】 D
12.【答案】 C
13.【答案】 C
14.【答案】 B
15.【答案】 A
16.【答案】 B
17.【答案】 B
18.【答案】 A
19.【答案】 B
20.【答案】 B
二、解答题
21.【答案】 (1)解:因为生产该款手机2万部并全部销售完时,年利润为704万美元.
所以 ,
解得 ,
当 时, ,
当 时, .
所以
(2)解:①当 时, ,所以 ;
②当 时, ,由于 ,
当且仅当 ,即 时,取等号,所以此时 的最大值为5760.
综合①②知,当 , 取得最大值为6104万美元.
22.【答案】 解:轮船从C到B用时80分钟,从B到E用时20分钟,
而船始终匀速前进,由此可见:BC=4EB,设EB= ,则
则BC=4 ,由已知得
在△AEC中,由正弦定理得:
在△ABC中,由正弦定理得:
在△ABE中,由余弦定理得:
所以船速 答:该船的速度为 km/h
23.【答案】 (1)因为 为偶函数.
所以 ,即 .
.
.
(2)由已知,方程 有且只有一个解.
有且只有一个解,且满足 .
整理得 .
令 ,则方程 在 有且只有一个实根.
当 时, ,不满足题意,舍去.
当 时,设方程对应的二次函数为 .
抛物线开口向上,对称轴 ,且 .
只需 ,则方程只有一个大于2 的根.
而 ,即 时满足题意.
当 时,抛物线开口向下,对称轴 ,且 .
此时方程无大于2 的实根.
综上 .
24.【答案】 (1)解:因为 ,
即 ,
所以 ,
所以 ,即 或 .
因为 ,所以 ,即 ;
(2)解:因为 与 垂直,
,
,
所以 ,因为 ,
所以 ,
即 .
同课章节目录
