5.4 平移 课件(共17张PPT)
图片预览




文档简介
(共17张PPT)
人教版 七年级下
5.4 平 移
精品同步教学课件
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础一般的学生使用。课件包括以下环节:
新知引入
典例讲解
新知学习
随堂练习
拓展提高
课堂小结
★ 平移的相关概念
探究 如何在一张半透明的纸上,画一排形状和大小都如图所示的雪人呢?
问题导入
思考:“雪人”的形状、大小、方向、位置在运动前后是否发生了变化?
形状不变,大小不变,方向不变,位置改变,记为“一变三不变”
平移的概念:在平面内,将一个图形整体沿某一直线方向移动一定的距离,这样的图形运动称为平移.
问题导入
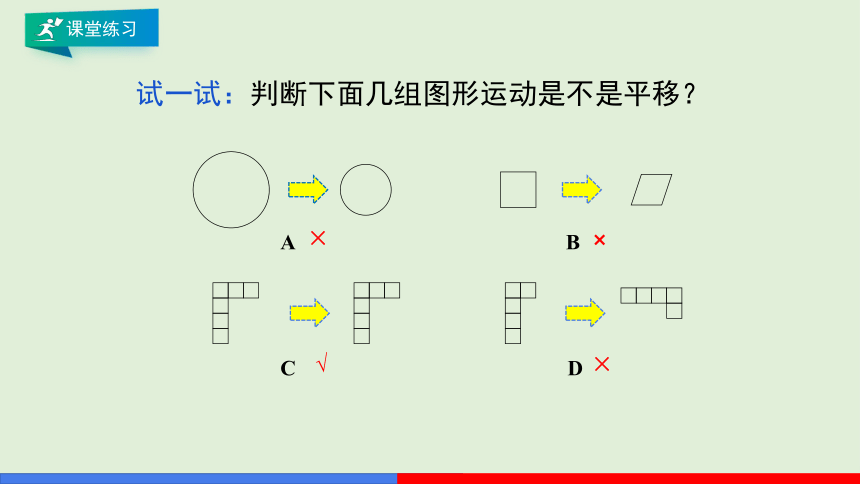
试一试:判断下面几组图形运动是不是平移?
A
C
D
B
×
×
√
×
课堂练习
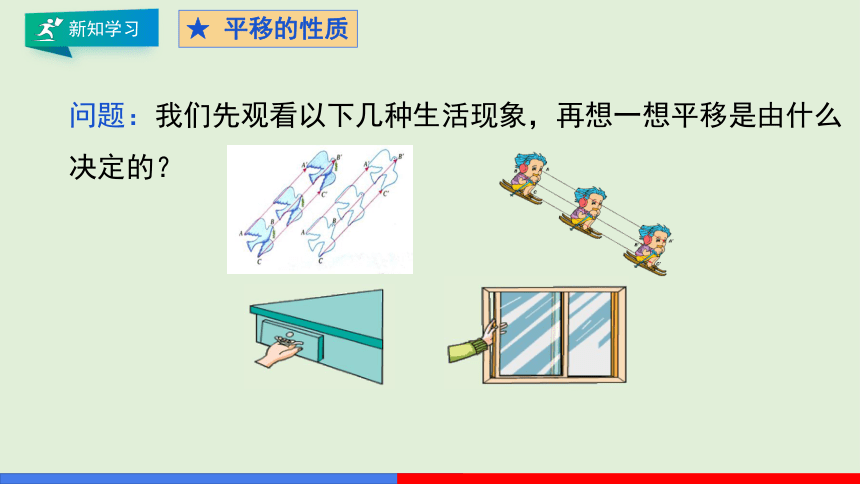
问题:我们先观看以下几种生活现象,再想一想平移是由什么决定的?
★ 平移的性质
新知学习
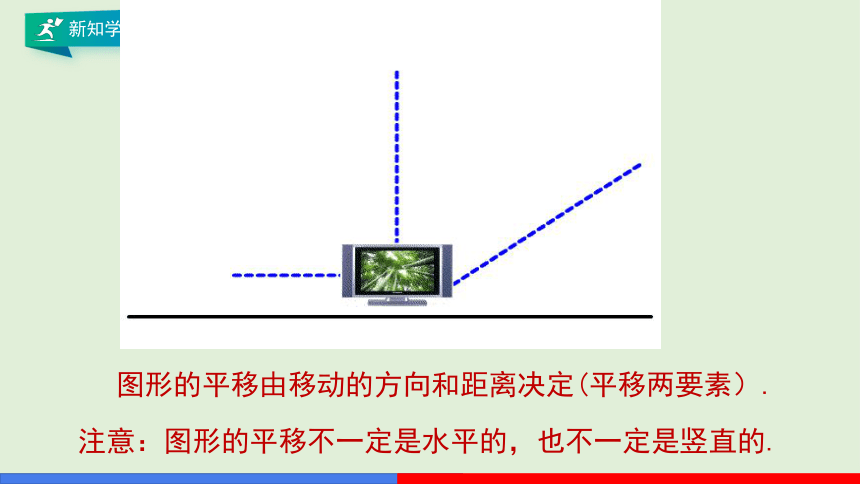
图形的平移由移动的方向和距离决定(平移两要素).
注意:图形的平移不一定是水平的,也不一定是竖直的.
新知学习
A
B
C
D
E
F
画一画:如图,平移三角形ABC,得到△DEF. 分析两个图形中的对应关系.
点 A、B、C的对应点分别是D、E、F;
线段AB、AC、BC的对应线段分别是DE、DF、EF.
新知学习
思考:上面图形中AD、BE、CF都有怎样的关系?
A
B
C
D
E
F
线段AD、BE、CF平行且相等.
⑴要想平移整个图形,需要把握图形上哪些关键的点?
⑵平移的方向是什么?
⑶平移的距离是谁的长度?
新知学习
动动手:用三角板、直尺画平行线.
P
Q
D
E
F
A
B
C
观察:线段AB与DE的位置关系与数量关系.
直尺PQ是倾斜放置,用三角板能否画 出平行线?
AB=DE
AB//DE
观察:线段AC与DF的位置关系与数量关系.
AC=DF
AC//DF
注意:在平移过程中,对应线段也可能在一条直线上(如:BC与EF)
新知学习
几何语言:
1.平移的两个图形形状和大小完全相同
A
B
C
D
E
F
∵三角形ABC平移得到三角形DEF,
∴AB∥DE,AC∥DF,BC ∥EF(或共线),
AB=DE,AC=DF,BC=EF,
AD∥BE∥CF(或共线),
AD=BE=CF.
∠A=∠D ∠B=∠E ∠C=∠F
2.对应线段平行(或在同一
直线上)且相等;
图形平移的性质:
3.各对应点所连线段平行
(或在同一直线上)且相等;
A
B
C
D
E
F
4.对应角相等
新知学习
例1 如图所示,经过平移,三角形ABC的顶点C移到了点C'.画出平移后的三角形A'B'C'的位置.并指出平移的方向和距离.
A
B
C
(1)连接CC';
(2)分别过点B,A按射线CC'的方向作线段BB',AA',使得它们与线段CC'平行且相等,连接A'C',A'B',B'C',三角形A'B'C'为所求;
(3)平移的方向就是点C到点C'的方向;
(4)平移的距离就是线段CC'的长度.
典例讲解
①找:先找出被平移图形的关键点(一般是图形顶点);
②定:确定平移的方向和距离;
③移:过关键点沿平移的方向作平行且相等的线段;
④连:按原图形顺次连接对应点。
平移一个图形的基本方法:
新知学习
1m
1m
21m
15m
A
C
D
B
图 1
1. 如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
1m
1m
21m
15m
A
C
D
B
图 1
解:长草部分的面积=(21-1)×(15-1)=280(m2).
课堂检测
2.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为___.
解:∵△ABC沿BC方向平移2cm得到△DEF,
∴CF=AD=2cm,AC=DF,
∵△ABC的周长为16cm,
∴AB+BC+AC=16cm,
∴四边形ABFD的周长=AB+BC+CF+DF+AD
=AB+BC+AC+CF+AD
=16cm+2cm+2cm
=20cm.
课堂检测
1m
21m
15m
A
C
D
B
3.如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
思路点拨:平移构成规则图形.
解:长草部分的面积=(21-1)×15=300(m2).
课堂检测
一找,二定,三移,四连
平移前后图形的形状和大小,完全相同
对应线段平行(或在同一直线上)且相等
平移的概念
平移的性质
平移作图
平移
各对应点所连线段平行(或在同一直线上)且相等
课堂小结
人教版 七年级下
5.4 平 移
精品同步教学课件
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础一般的学生使用。课件包括以下环节:
新知引入
典例讲解
新知学习
随堂练习
拓展提高
课堂小结
★ 平移的相关概念
探究 如何在一张半透明的纸上,画一排形状和大小都如图所示的雪人呢?
问题导入
思考:“雪人”的形状、大小、方向、位置在运动前后是否发生了变化?
形状不变,大小不变,方向不变,位置改变,记为“一变三不变”
平移的概念:在平面内,将一个图形整体沿某一直线方向移动一定的距离,这样的图形运动称为平移.
问题导入
试一试:判断下面几组图形运动是不是平移?
A
C
D
B
×
×
√
×
课堂练习
问题:我们先观看以下几种生活现象,再想一想平移是由什么决定的?
★ 平移的性质
新知学习
图形的平移由移动的方向和距离决定(平移两要素).
注意:图形的平移不一定是水平的,也不一定是竖直的.
新知学习
A
B
C
D
E
F
画一画:如图,平移三角形ABC,得到△DEF. 分析两个图形中的对应关系.
点 A、B、C的对应点分别是D、E、F;
线段AB、AC、BC的对应线段分别是DE、DF、EF.
新知学习
思考:上面图形中AD、BE、CF都有怎样的关系?
A
B
C
D
E
F
线段AD、BE、CF平行且相等.
⑴要想平移整个图形,需要把握图形上哪些关键的点?
⑵平移的方向是什么?
⑶平移的距离是谁的长度?
新知学习
动动手:用三角板、直尺画平行线.
P
Q
D
E
F
A
B
C
观察:线段AB与DE的位置关系与数量关系.
直尺PQ是倾斜放置,用三角板能否画 出平行线?
AB=DE
AB//DE
观察:线段AC与DF的位置关系与数量关系.
AC=DF
AC//DF
注意:在平移过程中,对应线段也可能在一条直线上(如:BC与EF)
新知学习
几何语言:
1.平移的两个图形形状和大小完全相同
A
B
C
D
E
F
∵三角形ABC平移得到三角形DEF,
∴AB∥DE,AC∥DF,BC ∥EF(或共线),
AB=DE,AC=DF,BC=EF,
AD∥BE∥CF(或共线),
AD=BE=CF.
∠A=∠D ∠B=∠E ∠C=∠F
2.对应线段平行(或在同一
直线上)且相等;
图形平移的性质:
3.各对应点所连线段平行
(或在同一直线上)且相等;
A
B
C
D
E
F
4.对应角相等
新知学习
例1 如图所示,经过平移,三角形ABC的顶点C移到了点C'.画出平移后的三角形A'B'C'的位置.并指出平移的方向和距离.
A
B
C
(1)连接CC';
(2)分别过点B,A按射线CC'的方向作线段BB',AA',使得它们与线段CC'平行且相等,连接A'C',A'B',B'C',三角形A'B'C'为所求;
(3)平移的方向就是点C到点C'的方向;
(4)平移的距离就是线段CC'的长度.
典例讲解
①找:先找出被平移图形的关键点(一般是图形顶点);
②定:确定平移的方向和距离;
③移:过关键点沿平移的方向作平行且相等的线段;
④连:按原图形顺次连接对应点。
平移一个图形的基本方法:
新知学习
1m
1m
21m
15m
A
C
D
B
图 1
1. 如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
1m
1m
21m
15m
A
C
D
B
图 1
解:长草部分的面积=(21-1)×(15-1)=280(m2).
课堂检测
2.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为___.
解:∵△ABC沿BC方向平移2cm得到△DEF,
∴CF=AD=2cm,AC=DF,
∵△ABC的周长为16cm,
∴AB+BC+AC=16cm,
∴四边形ABFD的周长=AB+BC+CF+DF+AD
=AB+BC+AC+CF+AD
=16cm+2cm+2cm
=20cm.
课堂检测
1m
21m
15m
A
C
D
B
3.如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
思路点拨:平移构成规则图形.
解:长草部分的面积=(21-1)×15=300(m2).
课堂检测
一找,二定,三移,四连
平移前后图形的形状和大小,完全相同
对应线段平行(或在同一直线上)且相等
平移的概念
平移的性质
平移作图
平移
各对应点所连线段平行(或在同一直线上)且相等
课堂小结
