冀教版 五年级数学下册第三单元 长方体和正方体(含答案)
文档属性
| 名称 | 冀教版 五年级数学下册第三单元 长方体和正方体(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 171.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 11:34:45 | ||
图片预览



文档简介
单元培优检测卷
第三单元 长方体和正方体
一、填空。(每空1分,共19分)
1.用铁丝焊接一个长是12厘米、宽是10厘米、高是6厘米的长方体框架,至少需要铁丝( )厘米。
2.如图是一个长方体展开图中的3个面。如果图中每个小方格的边长是1厘米,那么原来长方体的长是( )厘米,宽是( )厘米,高是( )厘米。
3.如图是一个长方体形状的牛奶包装箱。前面的面积是( )cm2;右面的面积是( )cm2;下面的面积是( )cm2;这三个面的面积之和是( )cm2;这个包装箱的表面积是( )cm2。
4.小明做了一个正方体框架。棱长总和是48厘米,这个正方体框架的棱长是( )厘米,在框架的外面糊上一层纸,至少要( )平方厘米的纸。
5.一个长方体包装箱,相交于一个顶点的三条棱的长度分别是
5分米、3分米、4分米。这个包装箱的占地面积最大是( )平方分米,它的表面积是( )平方分米。
6.如图,有7个棱长为5 cm的正方体放在墙角处。一共有( )个面露在外面,露在外面的面积是( )cm2。
7.用木板做两个长60厘米,宽50厘米,深18厘米的长方体抽屉,需要木板( )平方米。
8.有四个相同的正方体,按相同的规律在上面写上A、B、C、D、E、F这六个字母,然后如图摆放在一起,那么A的对面是( );B的对面是( );C的对面是( )。(不考虑字母的方向)
二、选择。(将正确答案的字母填在括号里)(每小题2分,共16分)
1.下列平面图形中,( )不能折成正方体。
2.如果一个长方体有两个相对的面是正方形,那么其余的面( )。
A.面积一定相等
B.面积不相等
C.有的相等,有的不相等
D.无法确定
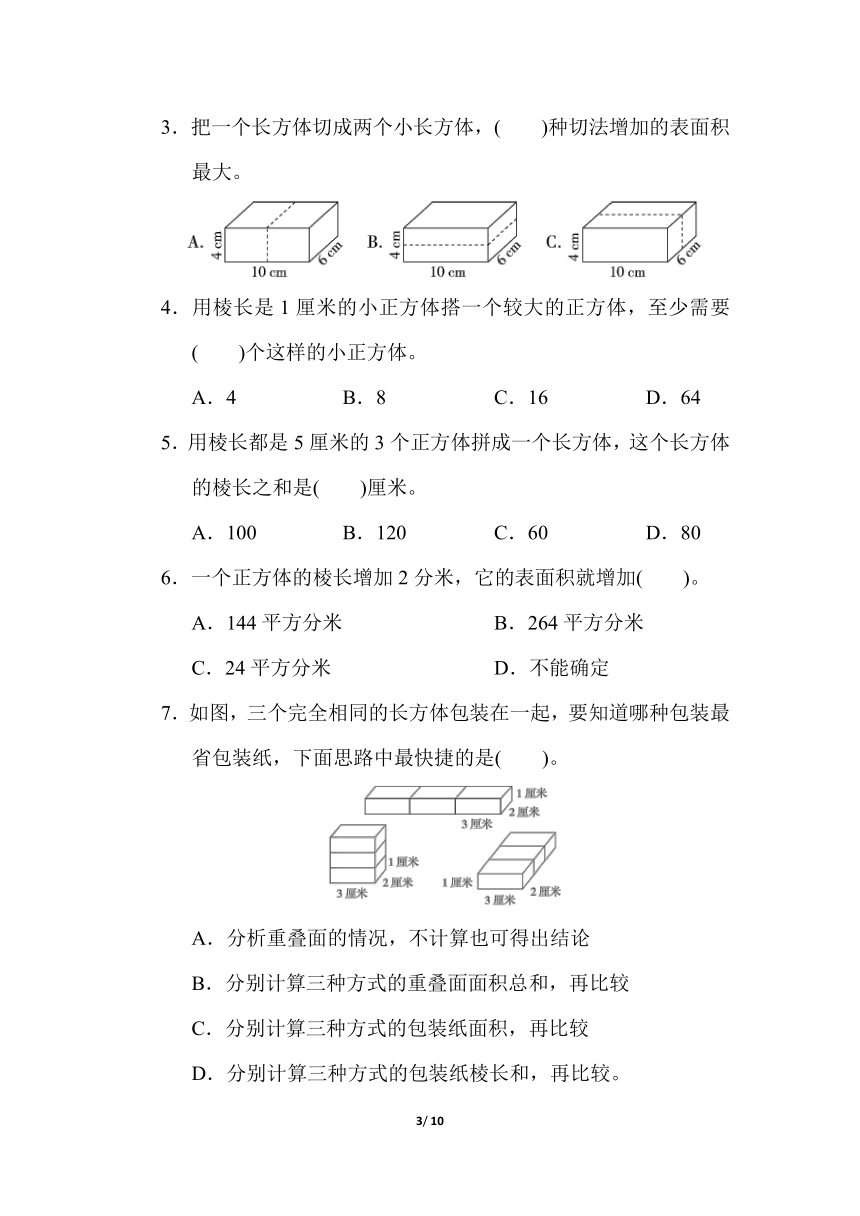
3.把一个长方体切成两个小长方体,( )种切法增加的表面积最大。
4.用棱长是1厘米的小正方体搭一个较大的正方体,至少需要( )个这样的小正方体。
A.4 B.8 C.16 D.64
5.用棱长都是5厘米的3个正方体拼成一个长方体,这个长方体的棱长之和是( )厘米。
A.100 B.120 C.60 D.80
6.一个正方体的棱长增加2分米,它的表面积就增加( )。
A.144平方分米 B.264平方分米
C.24平方分米 D.不能确定
7.如图,三个完全相同的长方体包装在一起,要知道哪种包装最省包装纸,下面思路中最快捷的是( )。
A.分析重叠面的情况,不计算也可得出结论
B.分别计算三种方式的重叠面面积总和,再比较
C.分别计算三种方式的包装纸面积,再比较
D.分别计算三种方式的包装纸棱长和,再比较。
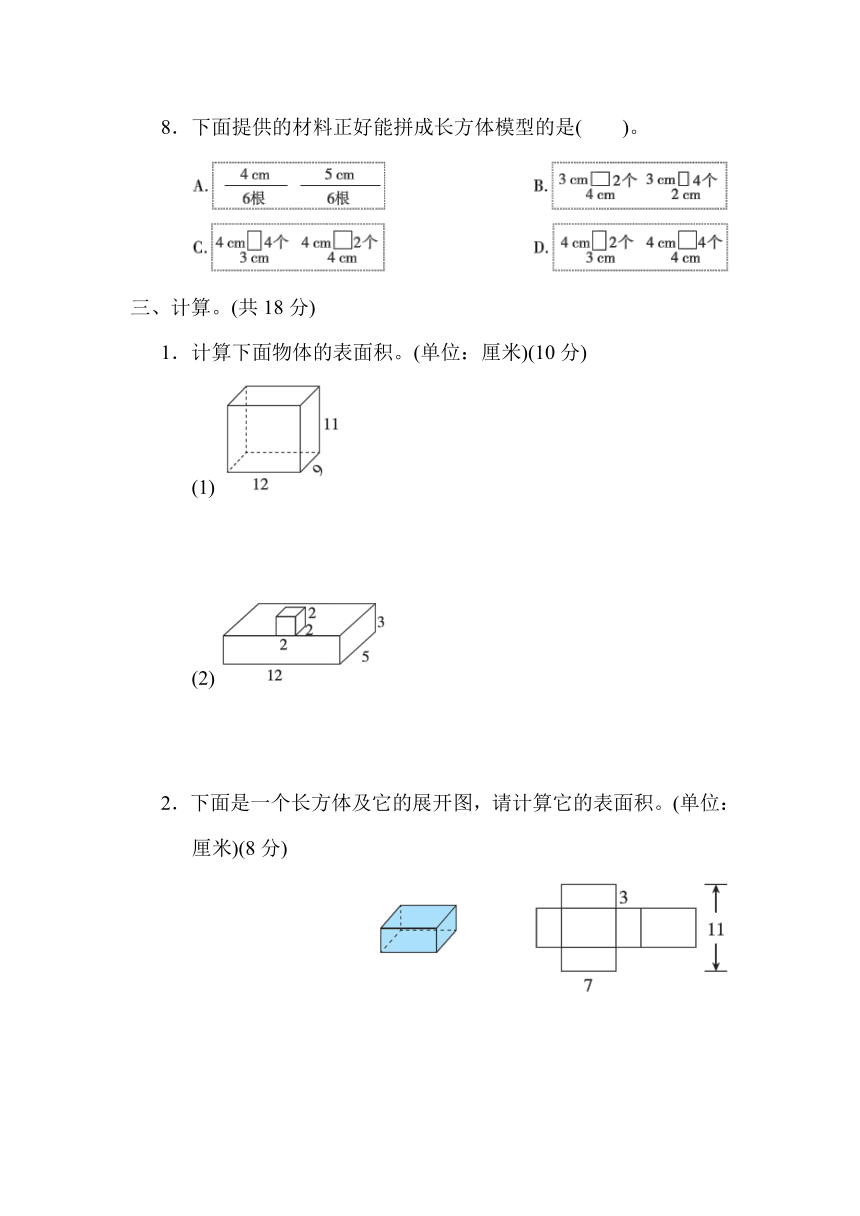
8.下面提供的材料正好能拼成长方体模型的是( )。
三、计算。(共18分)
1.计算下面物体的表面积。(单位:厘米)(10分)
(1)
(2)
2.下面是一个长方体及它的展开图,请计算它的表面积。(单位:厘米)(8分)
四、解决问题。(共47分)
1.石家庄某商业大楼为使夜间的宣传效果更好,请了工人师傅在长方体大楼的边上装上彩灯线(地面的四条边不装),已知大楼长80 m、宽50 m、高40 m,请你帮工人师傅算一算需要多少米彩灯线?(6分)
2.有一张长是40 cm,宽是35 cm的长方形铁皮,在它的4个角上分别剪去边长是5 cm的正方形(如下图所示),再将它焊接成一个无盖的长方体盒子。这个长方体盒子的表面积是多少?(6分)
3.育才小学建一个长方体游泳池,长20米,宽12米,深2米。请你算一算:
(1)游泳池占地多少平方米?(7分)
(2)在游泳池底面和内壁抹一层水泥,抹水泥的面积是多少平方米?(7分)
(3)在游泳池的内壁1.5米处用油漆画一条水位线,水位线全长多少米?(7分)
4.把一个正方体锯成两个长方体,它的表面积增加了32平方厘米,那么原来正方体的表面积是多少平方厘米?(7分)
5.唐山骨质瓷是河北省唐山市特产,也是中国国家地理标志产品。“薄如纸,白如玉,明如镜,声如磐”形象地概括了骨质瓷的四大特性。李叔叔要将4个装有骨质瓷的正方体礼品盒包装在一起有如图两种方案,哪种方案更节省包装纸?(注:4个正方体礼品盒的棱长都是3分米)(7分)
★附加题: 天才的你,试一试。(10分)
将两个同样大小的正方体拼在一起摆在桌面上(如图,单位:厘米),拼成的长方体的表面积是60平方厘米,你知道原来正方体的表面积吗?
答案
一、1.112 2.4 2 3
3.2000 1200 1500 4700 9400
4.4 96
5. 20 94
6. 13 325
7. 1.392 注意抽屉无上面。
8. F E D 由题图可知,与A相邻的面有B、C、D、E,则与A相对的面为F。与B相邻的面有A、C、D、F,则与B相对的面为E。与C相邻的面有A、B,且与A相对的面为F,与B相对的面为E,所以与C相对的面为D。
二、1.A 2.A 3.B 4.B 5.A 6.D
7.A 重叠面的面积越大,表面积越小,越省包装纸。
8.C
三、1.(1)(12×9+12×11+9×11)×2=678(平方厘米)
(2)(12×5+12×3+5×3)×2+2×2×4=238(平方厘米)
2. 长方体的宽为11-3×2=5(厘米)
(7×5+7×3+3×5)×2=142(平方厘米)
四、1.40×4+80×2+50×2=420(m)
答:需要420 m彩灯线。
2.40×35-5×5×4=1300(cm2)
答:这个长方体盒子的表面积是1300 cm2。
盒子的表面积就等于原铁皮面积减去剪去的4个正方形的面积和。
3.(1)20×12=240(平方米)
答:游泳池占地240平方米。
(2)20×12+20×2×2+12×2×2=368(平方米)
答:抹水泥的面积是368平方米。
(3)(20+12)×2=64(米)
答:水位线全长64米。
4.32÷2×6=96(平方厘米)
答:原来正方体的表面积是96平方厘米。
增加的表面积等于原正方体两个面的面积和。
5.方案A:3×2=6(分米)
(6×3+6×6+3×6)×2=144(平方分米)
方案B:3×4=12(分米)
(12×3+12×3+3×3)×2=162(平方分米)
答:方案A更节省包装纸。
附加题:10a2=60
a2= 6
6a2=6×6=36
答:原来正方体的表面积是36平方厘米。
1/ 10
第三单元 长方体和正方体
一、填空。(每空1分,共19分)
1.用铁丝焊接一个长是12厘米、宽是10厘米、高是6厘米的长方体框架,至少需要铁丝( )厘米。
2.如图是一个长方体展开图中的3个面。如果图中每个小方格的边长是1厘米,那么原来长方体的长是( )厘米,宽是( )厘米,高是( )厘米。
3.如图是一个长方体形状的牛奶包装箱。前面的面积是( )cm2;右面的面积是( )cm2;下面的面积是( )cm2;这三个面的面积之和是( )cm2;这个包装箱的表面积是( )cm2。
4.小明做了一个正方体框架。棱长总和是48厘米,这个正方体框架的棱长是( )厘米,在框架的外面糊上一层纸,至少要( )平方厘米的纸。
5.一个长方体包装箱,相交于一个顶点的三条棱的长度分别是
5分米、3分米、4分米。这个包装箱的占地面积最大是( )平方分米,它的表面积是( )平方分米。
6.如图,有7个棱长为5 cm的正方体放在墙角处。一共有( )个面露在外面,露在外面的面积是( )cm2。
7.用木板做两个长60厘米,宽50厘米,深18厘米的长方体抽屉,需要木板( )平方米。
8.有四个相同的正方体,按相同的规律在上面写上A、B、C、D、E、F这六个字母,然后如图摆放在一起,那么A的对面是( );B的对面是( );C的对面是( )。(不考虑字母的方向)
二、选择。(将正确答案的字母填在括号里)(每小题2分,共16分)
1.下列平面图形中,( )不能折成正方体。
2.如果一个长方体有两个相对的面是正方形,那么其余的面( )。
A.面积一定相等
B.面积不相等
C.有的相等,有的不相等
D.无法确定
3.把一个长方体切成两个小长方体,( )种切法增加的表面积最大。
4.用棱长是1厘米的小正方体搭一个较大的正方体,至少需要( )个这样的小正方体。
A.4 B.8 C.16 D.64
5.用棱长都是5厘米的3个正方体拼成一个长方体,这个长方体的棱长之和是( )厘米。
A.100 B.120 C.60 D.80
6.一个正方体的棱长增加2分米,它的表面积就增加( )。
A.144平方分米 B.264平方分米
C.24平方分米 D.不能确定
7.如图,三个完全相同的长方体包装在一起,要知道哪种包装最省包装纸,下面思路中最快捷的是( )。
A.分析重叠面的情况,不计算也可得出结论
B.分别计算三种方式的重叠面面积总和,再比较
C.分别计算三种方式的包装纸面积,再比较
D.分别计算三种方式的包装纸棱长和,再比较。
8.下面提供的材料正好能拼成长方体模型的是( )。
三、计算。(共18分)
1.计算下面物体的表面积。(单位:厘米)(10分)
(1)
(2)
2.下面是一个长方体及它的展开图,请计算它的表面积。(单位:厘米)(8分)
四、解决问题。(共47分)
1.石家庄某商业大楼为使夜间的宣传效果更好,请了工人师傅在长方体大楼的边上装上彩灯线(地面的四条边不装),已知大楼长80 m、宽50 m、高40 m,请你帮工人师傅算一算需要多少米彩灯线?(6分)
2.有一张长是40 cm,宽是35 cm的长方形铁皮,在它的4个角上分别剪去边长是5 cm的正方形(如下图所示),再将它焊接成一个无盖的长方体盒子。这个长方体盒子的表面积是多少?(6分)
3.育才小学建一个长方体游泳池,长20米,宽12米,深2米。请你算一算:
(1)游泳池占地多少平方米?(7分)
(2)在游泳池底面和内壁抹一层水泥,抹水泥的面积是多少平方米?(7分)
(3)在游泳池的内壁1.5米处用油漆画一条水位线,水位线全长多少米?(7分)
4.把一个正方体锯成两个长方体,它的表面积增加了32平方厘米,那么原来正方体的表面积是多少平方厘米?(7分)
5.唐山骨质瓷是河北省唐山市特产,也是中国国家地理标志产品。“薄如纸,白如玉,明如镜,声如磐”形象地概括了骨质瓷的四大特性。李叔叔要将4个装有骨质瓷的正方体礼品盒包装在一起有如图两种方案,哪种方案更节省包装纸?(注:4个正方体礼品盒的棱长都是3分米)(7分)
★附加题: 天才的你,试一试。(10分)
将两个同样大小的正方体拼在一起摆在桌面上(如图,单位:厘米),拼成的长方体的表面积是60平方厘米,你知道原来正方体的表面积吗?
答案
一、1.112 2.4 2 3
3.2000 1200 1500 4700 9400
4.4 96
5. 20 94
6. 13 325
7. 1.392 注意抽屉无上面。
8. F E D 由题图可知,与A相邻的面有B、C、D、E,则与A相对的面为F。与B相邻的面有A、C、D、F,则与B相对的面为E。与C相邻的面有A、B,且与A相对的面为F,与B相对的面为E,所以与C相对的面为D。
二、1.A 2.A 3.B 4.B 5.A 6.D
7.A 重叠面的面积越大,表面积越小,越省包装纸。
8.C
三、1.(1)(12×9+12×11+9×11)×2=678(平方厘米)
(2)(12×5+12×3+5×3)×2+2×2×4=238(平方厘米)
2. 长方体的宽为11-3×2=5(厘米)
(7×5+7×3+3×5)×2=142(平方厘米)
四、1.40×4+80×2+50×2=420(m)
答:需要420 m彩灯线。
2.40×35-5×5×4=1300(cm2)
答:这个长方体盒子的表面积是1300 cm2。
盒子的表面积就等于原铁皮面积减去剪去的4个正方形的面积和。
3.(1)20×12=240(平方米)
答:游泳池占地240平方米。
(2)20×12+20×2×2+12×2×2=368(平方米)
答:抹水泥的面积是368平方米。
(3)(20+12)×2=64(米)
答:水位线全长64米。
4.32÷2×6=96(平方厘米)
答:原来正方体的表面积是96平方厘米。
增加的表面积等于原正方体两个面的面积和。
5.方案A:3×2=6(分米)
(6×3+6×6+3×6)×2=144(平方分米)
方案B:3×4=12(分米)
(12×3+12×3+3×3)×2=162(平方分米)
答:方案A更节省包装纸。
附加题:10a2=60
a2= 6
6a2=6×6=36
答:原来正方体的表面积是36平方厘米。
1/ 10
