2021-2022学年高一上学期数学沪教版(2020)必修第一册期末复习第 4 章 幂函数、指数函数与对数函数 填充、选择题测试【1】
文档属性
| 名称 | 2021-2022学年高一上学期数学沪教版(2020)必修第一册期末复习第 4 章 幂函数、指数函数与对数函数 填充、选择题测试【1】 |

|
|
| 格式 | doc | ||
| 文件大小 | 410.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 17:31:26 | ||
图片预览


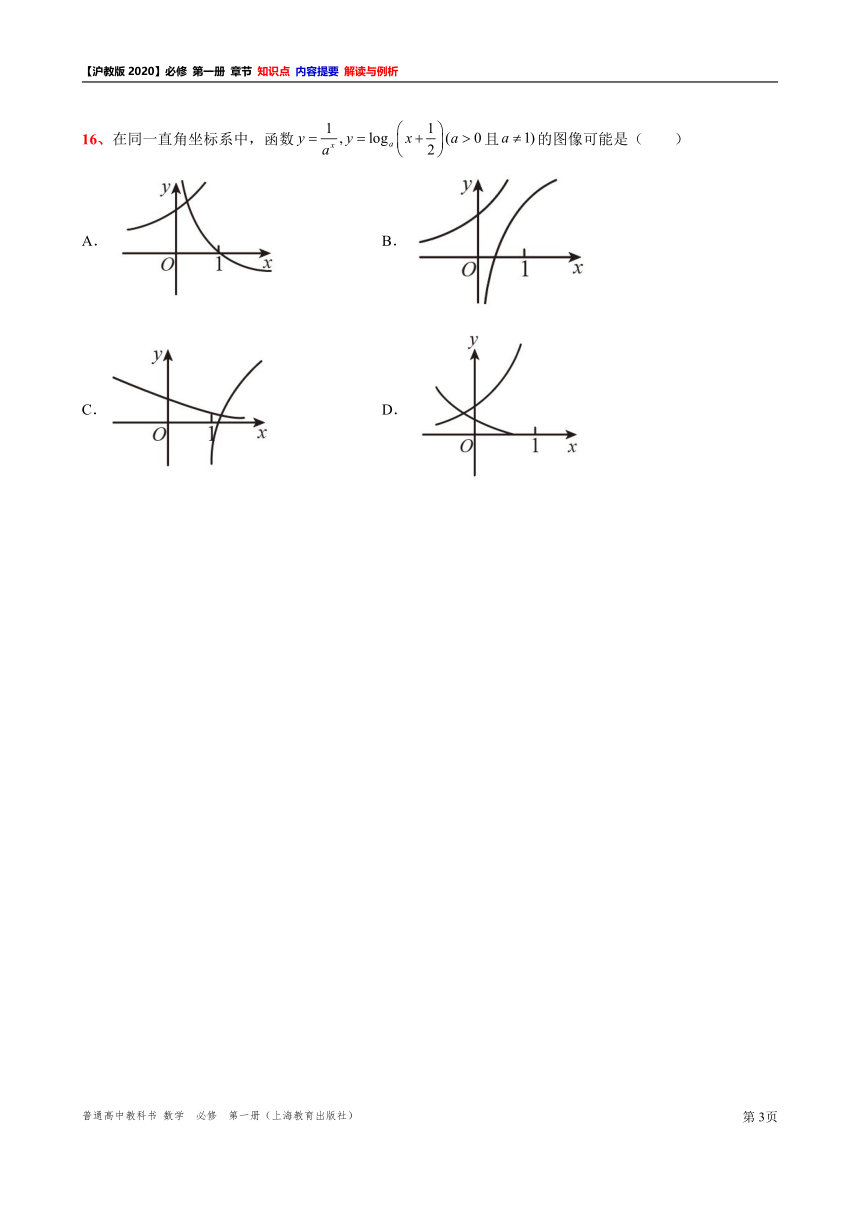

文档简介
【沪教版2020】必修 第一册 章节 知识点 内容提要 解读与例析
【学生版】
《第 4 章 幂函数、指数函数与对数函数》填充、选择题测试【1】
一、填空题(本大题共有12题,满分36分)只要求直接填写结果,每个空格填对得3分,
否则一律得零分.
1、设集合A={x||x-1|<2},B={y|y=2x,x∈[0,2]},则A∩B=
【提示】
【答案】
【解析】
【说明】
2、若幂函数是偶函数,则实数m=
【提示】
【答案】
【解析】
【说明】
3、已知幂函数的图像经过点,则等于
【提示】
【答案】
【解析】
【说明】
4、已知(为常数)的图像经过点,则的值为
【提示】
【答案】
【解析】
【说明】
5、已知函数,若图像过点,则的值为
【提示】
【答案】
【解析】
【说明】
6、函数y=loga(x-1)+2(a>0,且a≠1)的图像恒过的定点是________.
7、已知函数f(x)=lg x,若f(ab)=1,则f(a2)+f(b2)=________
8、已知函数f(x)=loga(8-ax)(a>0,且a≠1),若f(x)>1在区间[1,2]上恒成立,则实数a的取值范围是__________
9、若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)等于
10、已知函数f(x)=|(m为常数),若f(x)在区间[2,+∞)上是增加的,则m的取值范围是_____
11、若函数f(x)=的值域是,则f(x)的单调递增区间是
12、若函数在上单调,则实数的取值范围是
二、选择题(本大题共有4题,满分12分) 每小题都给出四个选项,其中有且只有一个选项是正确的,选对
得 3分,否则一律得零分.
13、函数f(x)=log2(x2-2x-8)的单调递减区间是( )
A.(-∞,-2) B.(-∞,-1) C.(1,+∞) D.(4,+∞)
【提示】
【答案】
【解析】
【说明】
14、已知函数f(x)=2|x|,且f(log2m)>f(2),则实数m的取值范围为( )
A.(4,+∞) B. C. ∪(4,+∞) D. ∪(4,+∞)
15、已知函数f(x)=x2+log2|x|,则不等式f(x-1)-f(1)<0的解集为( )
A.(0,2) B.(-1,2)[来C.(0,1)∪(1,2) D.(-1,1)∪(1,3)
16、在同一直角坐标系中,函数且的图像可能是( )
A. B.
C. D.
【教师版】
《第 4 章 幂函数、指数函数与对数函数》填充、选择题测试【1】
一、填空题(本大题共有12题,满分36分)只要求直接填写结果,每个空格填对得3分,
否则一律得零分.
1、设集合A={x||x-1|<2},B={y|y=2x,x∈[0,2]},则A∩B=
【提示】先利用指数函数性质进行化简集合;
【答案】[1,3)
【解析】由题意,得A={x||x-1|<2}={x|-1【说明】本题是指数函数的性质与集合运算的交汇;
2、若幂函数是偶函数,则实数m=
【提示】理解幂函数定义与偶函数的定义;
【答案】-1;
【解析】因为f(x)=(m2-m-1)·x1-m为幂函数,所以m2-m-1=1解得m=-1或2,又f(x)是偶函数,则1-m为偶数.故m=-1;
【说明】本题综合考查了幂函数定义与偶函数的定义的代数表示;
3、已知幂函数的图像经过点,则等于
【提示】注意:函数表示方法间的转换;
【答案】;
【解析】因为为幂函数,所以,所以,因为幂函数的图像过点,
所以,解得,所以;
【说明】本题以幂函数为载体考查了:函数解析式与图像之间的联系与互化;
4、已知(为常数)的图像经过点,则的值为
【提示】注意:函数表示方法间的转换;
【答案】9;
【解析】,即,;
【说明】本题以指数函数为载体考查了:函数解析式与图像之间的联系与互化;
5、已知函数,若图像过点,则的值为
【提示】注意:函数表示方法间的转换;
【答案】2;
【解析】因为函数的 图象过点,所以,
则,所以,,
【说明】本题以对数函数为载体考查了:函数解析式与图像之间的联系与互化;
6、函数y=loga(x-1)+2(a>0,且a≠1)的图像恒过的定点是________.
【提示】注意:对数函数的图像特征;
【答案】(2,2)
【解析】由x-1=1,得x=2,则y=2;
【说明】本题主要考查函数的图像与“代换法”;
7、已知函数f(x)=lg x,若f(ab)=1,则f(a2)+f(b2)=________
【提示】注意:函数定义域与已知自变量求值;
【答案】2;
【解析】f(ab)=1 lg ab=1,f(a2)+f(b2)=lg a2+lg b2=2lg ab=2;
【说明】本题考查了对数函数与对数运算;
8、已知函数f(x)=loga(8-ax)(a>0,且a≠1),若f(x)>1在区间[1,2]上恒成立,则实数a的取值范围是__________
【提示】注意:等价转化;
【答案】 ;
【解析】当a>1时,f(x)=loga(8-ax)在[1,2]上单调递减,由f(x)>1在区间[1,2]上恒成立,
则f(x)min=f(2)=loga(8-2a)>1,且8-2a>0,解得1当01在区间[1,2]上恒成立,
知f(x)min=f(1)=loga(8-a)>1,且8-2a>0.;解得a∈ ,
综上可知,实数a的取值范围是.
【说明】本题考查了对数函数与复合函数的单调性;并与等价转化、解不等式进行了交汇;
9、若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)等于
【提示】注意:原函数与反函数之间的联系;
【答案】log2x;
【解析】由y=ax的反函数为f(x)=logax,则1=loga2,所以a=2,所以f(x)=log2x;
【说明】本题主要考查了指数函数的反函数是对数函数;
10、已知函数f(x)=|(m为常数),若f(x)在区间[2,+∞)上是增加的,则m的取值范围是_____
【提示】注意:将已知函数分解成若干初等函数;
【答案】(-∞,4];
【解析】令t=|2x-m|,则t=|2x-m|在区间上是增加的,
在区间上是减少的;
而y=2t在R上是增加的,所以要使函数f(x)=2|2x-m|在[2,+∞)上是增加的,
则有≤2,即m≤4,所以m的取值范围是(-∞,4];
【说明】本题主要依据:一次函数与指数函数的单调性进行等价转化;
11、若函数f(x)=的值域是,则f(x)的单调递增区间是
【提示】注意:将已知函数分解成若干初等函数;
【答案】(-∞,-1];
【解析】令g(x)=ax2+2x+3,由于f(x)的值域是,所以g(x)的值域是[2,+∞).
因此有解得a=1,这时g(x)=x2+2x+3,f(x)=.
由于g(x)的单调递减区间是(-∞,-1],所以f(x)的单调递增区间是(-∞,-1];
【说明】本题主要依据:一元二次次函数与指数函数的单调性进行等价转化,求值域;强调规范解题求参数,然后,利用复合函数求单调区间;
12、若函数在上单调,则实数的取值范围是
【提示】注意:遇对数先保证有意义;
【答案】;
【解析】函数在上单调,函数的定义域为,
因为,在上单调递增,在上单调递减,
在定义域上单调递增,所以在上单调递增,在上单调递减,
要使函数在上单调,
所以,,或,解得,或,即;
【说明】本题综合考查了函数的定义域,复合函数的单调性与等价转化思想;
二、选择题(本大题共有4题,满分12分) 每小题都给出四个选项,其中有且只有一个选项是正确的,选对
得 3分,否则一律得零分.
13、函数f(x)=log2(x2-2x-8)的单调递减区间是( )
A.(-∞,-2) B.(-∞,-1) C.(1,+∞) D.(4,+∞)
【提示】注意:分解复合函数;
【答案】A;
【解析】由x2-2x-8>0,得x∈(-∞,-2)∪(4,+∞);令t=x2-x-8,则y=log2t.
当x∈(-∞,-2)时,t=x2-2x-8=(x-1)2-9为减函数,y=log2t为增函数,
所以,f(x)=log2(x2-2x-8)为减函数;
当x∈(4,+∞)时,t=x2-2x-8=(x-1)2-9为增函数,y=log2t为增函数,
所以,f(x)=log2(x2-2x-8)为增函数;
故函数f(x)=ln(x2-2x-8)的单调递减区间是(-∞,-2);
【说明】本题考查了对数函数的定义域;一元二次函数、对数函数、复合函数的单调性;
14、已知函数f(x)=2|x|,且f(log2m)>f(2),则实数m的取值范围为( )
A.(4,+∞) B. C. ∪(4,+∞) D. ∪(4,+∞)
【提示】注意:利用初等函数图像变换进行等价转化;
【答案】D;
【解析】由题意知函数f(x)=2|x|为偶函数,且在(-∞,0)上单调递减,在(0,+∞)上单调递增;
因为,f(log2m)>f(2),所以,|log2m|>2,即log2m>2或log2m<-2,解得m>4或0所以,实数m的取值范围为∪(4,+∞);故选D;
【说明】本题综合考查了函数的性质,利用等价转化思想进行等价转化;
15、已知函数f(x)=x2+log2|x|,则不等式f(x-1)-f(1)<0的解集为( )
A.(0,2) B.(-1,2)[来C.(0,1)∪(1,2) D.(-1,1)∪(1,3)
【提示】注意:研究函数的性质;
【答案】C;
【解析】由题意知函数f(x)=x2+log2|x|为偶函数,且在(0,+∞)上单调递增;
由f(x-1)-f(1)<0可得f(x-1)又x-1≠0,即x≠1,所以,0故不等式的解集为(0,1)∪(1,2);故选C;
【说明】本题考查了研究函数性质的方法与性质的综合应用;
16、在同一直角坐标系中,函数且的图像可能是( )
A. B.
C. D.
【提示】注意:根据一个初等函数的图像信息,再验证确定第2个函数图像;
【答案】D;
【解析】当时,函数过定点且单调递减,则函数过定点且单调递增,函数过定点且单调递减,D选项符合;当时,函数过定点且单调递增,则函数过定点且单调递减,函数过定点且单调递增,各选项均不符合.综上,选D;
【说明】本题通过讨论的不同取值情况,分别讨论本题指数函数、对数函数的图象和,结合选项,判断得出正确结论.题目不难,注重重要知识、基础知识、逻辑推理能力的考查
附:函数图像的识别及应用方法
(1)在识别函数图像时,要善于利用已知函数的性质、函数图像上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项;
(2)一些指数、对数型方程、不等式问题常转化为相应的函数图像问题,利用数形结合法求解;
PAGE
第4页
普通高中教科书 数学 必修 第一册(上海教育出版社)
【学生版】
《第 4 章 幂函数、指数函数与对数函数》填充、选择题测试【1】
一、填空题(本大题共有12题,满分36分)只要求直接填写结果,每个空格填对得3分,
否则一律得零分.
1、设集合A={x||x-1|<2},B={y|y=2x,x∈[0,2]},则A∩B=
【提示】
【答案】
【解析】
【说明】
2、若幂函数是偶函数,则实数m=
【提示】
【答案】
【解析】
【说明】
3、已知幂函数的图像经过点,则等于
【提示】
【答案】
【解析】
【说明】
4、已知(为常数)的图像经过点,则的值为
【提示】
【答案】
【解析】
【说明】
5、已知函数,若图像过点,则的值为
【提示】
【答案】
【解析】
【说明】
6、函数y=loga(x-1)+2(a>0,且a≠1)的图像恒过的定点是________.
7、已知函数f(x)=lg x,若f(ab)=1,则f(a2)+f(b2)=________
8、已知函数f(x)=loga(8-ax)(a>0,且a≠1),若f(x)>1在区间[1,2]上恒成立,则实数a的取值范围是__________
9、若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)等于
10、已知函数f(x)=|(m为常数),若f(x)在区间[2,+∞)上是增加的,则m的取值范围是_____
11、若函数f(x)=的值域是,则f(x)的单调递增区间是
12、若函数在上单调,则实数的取值范围是
二、选择题(本大题共有4题,满分12分) 每小题都给出四个选项,其中有且只有一个选项是正确的,选对
得 3分,否则一律得零分.
13、函数f(x)=log2(x2-2x-8)的单调递减区间是( )
A.(-∞,-2) B.(-∞,-1) C.(1,+∞) D.(4,+∞)
【提示】
【答案】
【解析】
【说明】
14、已知函数f(x)=2|x|,且f(log2m)>f(2),则实数m的取值范围为( )
A.(4,+∞) B. C. ∪(4,+∞) D. ∪(4,+∞)
15、已知函数f(x)=x2+log2|x|,则不等式f(x-1)-f(1)<0的解集为( )
A.(0,2) B.(-1,2)[来C.(0,1)∪(1,2) D.(-1,1)∪(1,3)
16、在同一直角坐标系中,函数且的图像可能是( )
A. B.
C. D.
【教师版】
《第 4 章 幂函数、指数函数与对数函数》填充、选择题测试【1】
一、填空题(本大题共有12题,满分36分)只要求直接填写结果,每个空格填对得3分,
否则一律得零分.
1、设集合A={x||x-1|<2},B={y|y=2x,x∈[0,2]},则A∩B=
【提示】先利用指数函数性质进行化简集合;
【答案】[1,3)
【解析】由题意,得A={x||x-1|<2}={x|-1
2、若幂函数是偶函数,则实数m=
【提示】理解幂函数定义与偶函数的定义;
【答案】-1;
【解析】因为f(x)=(m2-m-1)·x1-m为幂函数,所以m2-m-1=1解得m=-1或2,又f(x)是偶函数,则1-m为偶数.故m=-1;
【说明】本题综合考查了幂函数定义与偶函数的定义的代数表示;
3、已知幂函数的图像经过点,则等于
【提示】注意:函数表示方法间的转换;
【答案】;
【解析】因为为幂函数,所以,所以,因为幂函数的图像过点,
所以,解得,所以;
【说明】本题以幂函数为载体考查了:函数解析式与图像之间的联系与互化;
4、已知(为常数)的图像经过点,则的值为
【提示】注意:函数表示方法间的转换;
【答案】9;
【解析】,即,;
【说明】本题以指数函数为载体考查了:函数解析式与图像之间的联系与互化;
5、已知函数,若图像过点,则的值为
【提示】注意:函数表示方法间的转换;
【答案】2;
【解析】因为函数的 图象过点,所以,
则,所以,,
【说明】本题以对数函数为载体考查了:函数解析式与图像之间的联系与互化;
6、函数y=loga(x-1)+2(a>0,且a≠1)的图像恒过的定点是________.
【提示】注意:对数函数的图像特征;
【答案】(2,2)
【解析】由x-1=1,得x=2,则y=2;
【说明】本题主要考查函数的图像与“代换法”;
7、已知函数f(x)=lg x,若f(ab)=1,则f(a2)+f(b2)=________
【提示】注意:函数定义域与已知自变量求值;
【答案】2;
【解析】f(ab)=1 lg ab=1,f(a2)+f(b2)=lg a2+lg b2=2lg ab=2;
【说明】本题考查了对数函数与对数运算;
8、已知函数f(x)=loga(8-ax)(a>0,且a≠1),若f(x)>1在区间[1,2]上恒成立,则实数a的取值范围是__________
【提示】注意:等价转化;
【答案】 ;
【解析】当a>1时,f(x)=loga(8-ax)在[1,2]上单调递减,由f(x)>1在区间[1,2]上恒成立,
则f(x)min=f(2)=loga(8-2a)>1,且8-2a>0,解得1
知f(x)min=f(1)=loga(8-a)>1,且8-2a>0.;解得a∈ ,
综上可知,实数a的取值范围是.
【说明】本题考查了对数函数与复合函数的单调性;并与等价转化、解不等式进行了交汇;
9、若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)等于
【提示】注意:原函数与反函数之间的联系;
【答案】log2x;
【解析】由y=ax的反函数为f(x)=logax,则1=loga2,所以a=2,所以f(x)=log2x;
【说明】本题主要考查了指数函数的反函数是对数函数;
10、已知函数f(x)=|(m为常数),若f(x)在区间[2,+∞)上是增加的,则m的取值范围是_____
【提示】注意:将已知函数分解成若干初等函数;
【答案】(-∞,4];
【解析】令t=|2x-m|,则t=|2x-m|在区间上是增加的,
在区间上是减少的;
而y=2t在R上是增加的,所以要使函数f(x)=2|2x-m|在[2,+∞)上是增加的,
则有≤2,即m≤4,所以m的取值范围是(-∞,4];
【说明】本题主要依据:一次函数与指数函数的单调性进行等价转化;
11、若函数f(x)=的值域是,则f(x)的单调递增区间是
【提示】注意:将已知函数分解成若干初等函数;
【答案】(-∞,-1];
【解析】令g(x)=ax2+2x+3,由于f(x)的值域是,所以g(x)的值域是[2,+∞).
因此有解得a=1,这时g(x)=x2+2x+3,f(x)=.
由于g(x)的单调递减区间是(-∞,-1],所以f(x)的单调递增区间是(-∞,-1];
【说明】本题主要依据:一元二次次函数与指数函数的单调性进行等价转化,求值域;强调规范解题求参数,然后,利用复合函数求单调区间;
12、若函数在上单调,则实数的取值范围是
【提示】注意:遇对数先保证有意义;
【答案】;
【解析】函数在上单调,函数的定义域为,
因为,在上单调递增,在上单调递减,
在定义域上单调递增,所以在上单调递增,在上单调递减,
要使函数在上单调,
所以,,或,解得,或,即;
【说明】本题综合考查了函数的定义域,复合函数的单调性与等价转化思想;
二、选择题(本大题共有4题,满分12分) 每小题都给出四个选项,其中有且只有一个选项是正确的,选对
得 3分,否则一律得零分.
13、函数f(x)=log2(x2-2x-8)的单调递减区间是( )
A.(-∞,-2) B.(-∞,-1) C.(1,+∞) D.(4,+∞)
【提示】注意:分解复合函数;
【答案】A;
【解析】由x2-2x-8>0,得x∈(-∞,-2)∪(4,+∞);令t=x2-x-8,则y=log2t.
当x∈(-∞,-2)时,t=x2-2x-8=(x-1)2-9为减函数,y=log2t为增函数,
所以,f(x)=log2(x2-2x-8)为减函数;
当x∈(4,+∞)时,t=x2-2x-8=(x-1)2-9为增函数,y=log2t为增函数,
所以,f(x)=log2(x2-2x-8)为增函数;
故函数f(x)=ln(x2-2x-8)的单调递减区间是(-∞,-2);
【说明】本题考查了对数函数的定义域;一元二次函数、对数函数、复合函数的单调性;
14、已知函数f(x)=2|x|,且f(log2m)>f(2),则实数m的取值范围为( )
A.(4,+∞) B. C. ∪(4,+∞) D. ∪(4,+∞)
【提示】注意:利用初等函数图像变换进行等价转化;
【答案】D;
【解析】由题意知函数f(x)=2|x|为偶函数,且在(-∞,0)上单调递减,在(0,+∞)上单调递增;
因为,f(log2m)>f(2),所以,|log2m|>2,即log2m>2或log2m<-2,解得m>4或0
【说明】本题综合考查了函数的性质,利用等价转化思想进行等价转化;
15、已知函数f(x)=x2+log2|x|,则不等式f(x-1)-f(1)<0的解集为( )
A.(0,2) B.(-1,2)[来C.(0,1)∪(1,2) D.(-1,1)∪(1,3)
【提示】注意:研究函数的性质;
【答案】C;
【解析】由题意知函数f(x)=x2+log2|x|为偶函数,且在(0,+∞)上单调递增;
由f(x-1)-f(1)<0可得f(x-1)
【说明】本题考查了研究函数性质的方法与性质的综合应用;
16、在同一直角坐标系中,函数且的图像可能是( )
A. B.
C. D.
【提示】注意:根据一个初等函数的图像信息,再验证确定第2个函数图像;
【答案】D;
【解析】当时,函数过定点且单调递减,则函数过定点且单调递增,函数过定点且单调递减,D选项符合;当时,函数过定点且单调递增,则函数过定点且单调递减,函数过定点且单调递增,各选项均不符合.综上,选D;
【说明】本题通过讨论的不同取值情况,分别讨论本题指数函数、对数函数的图象和,结合选项,判断得出正确结论.题目不难,注重重要知识、基础知识、逻辑推理能力的考查
附:函数图像的识别及应用方法
(1)在识别函数图像时,要善于利用已知函数的性质、函数图像上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项;
(2)一些指数、对数型方程、不等式问题常转化为相应的函数图像问题,利用数形结合法求解;
PAGE
第4页
普通高中教科书 数学 必修 第一册(上海教育出版社)
