2021-2022学年高一上学期数学沪教版(2020)必修第一册期末复习第 4 章 幂函数、指数函数与对数函数 填充、选择题测试【3】
文档属性
| 名称 | 2021-2022学年高一上学期数学沪教版(2020)必修第一册期末复习第 4 章 幂函数、指数函数与对数函数 填充、选择题测试【3】 |  | |
| 格式 | doc | ||
| 文件大小 | 434.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 17:33:22 | ||
图片预览




文档简介
【沪教版2020】必修 第一册 章节 知识点 内容提要 解读与例析
【学生版】
《第 4 章 幂函数、指数函数与对数函数》填充、选择题测试【3】
一、填空题(本大题共有12题,满分36分)只要求直接填写结果,每个空格填对得3分,
否则一律得零分.
1、若幂函数的图像与坐标轴无公共点,且关于原点对称,则实数m的取值集合为
【提示】
【答案】
【解析】
【说明】
2、若函数f(x)=(a>0,a≠1)满足f(1)=,则f(x)的单调递减区间是
【提示】
【答案】
【解析】
【说明】
3、已知函数y=f(x)的定义域为(1,2),则函数y=f(2x)的定义域为________
【提示】
【答案】
【解析】
【说明】
4、已知函数f(x)=ax+b的图像过(1,7),其反函数 的图像过点(4,0),则f(x)的表达式为f(x)=
【提示】
【答案】
【解析】
【说明】
5、若函数f(x)=(a>0,且a≠1)的值域是[4,+∞),则实数a的取值范围是________
【提示】
【答案】
【解析】
【说明】
6、已知函数f(x)=|log2x|,正实数m,n满足m7、已知max{a,b}表示a,b两数中的最大值.若f(x)=max{e|x|,e|x-2|},则f(x)的最小值为________
8、设函数f(x)=x2-a与g(x)=ax(a>1且a≠2)在区间(0,+∞)上具有不同的单调性,
则M=(a-1)0.2与N=0.1的大小关系是
9、已知函数f(x)=关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是________.
10、若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围是________
11、已知函数f(x)=|log2x|,实数a,b满足012、若函数y=|2x-1|在(-∞,m]上单调递减,则m的取值范围是
二、选择题(本大题共有4题,满分12分) 每小题都给出四个选项,其中有且只有一个选项是正确的,选对
得 3分,否则一律得零分.
13、在同一直角坐标系中,函数f(x)=xa(x>0),g(x)=logax的图象可能是( )
【提示】
【答案】
【解析】
【说明】
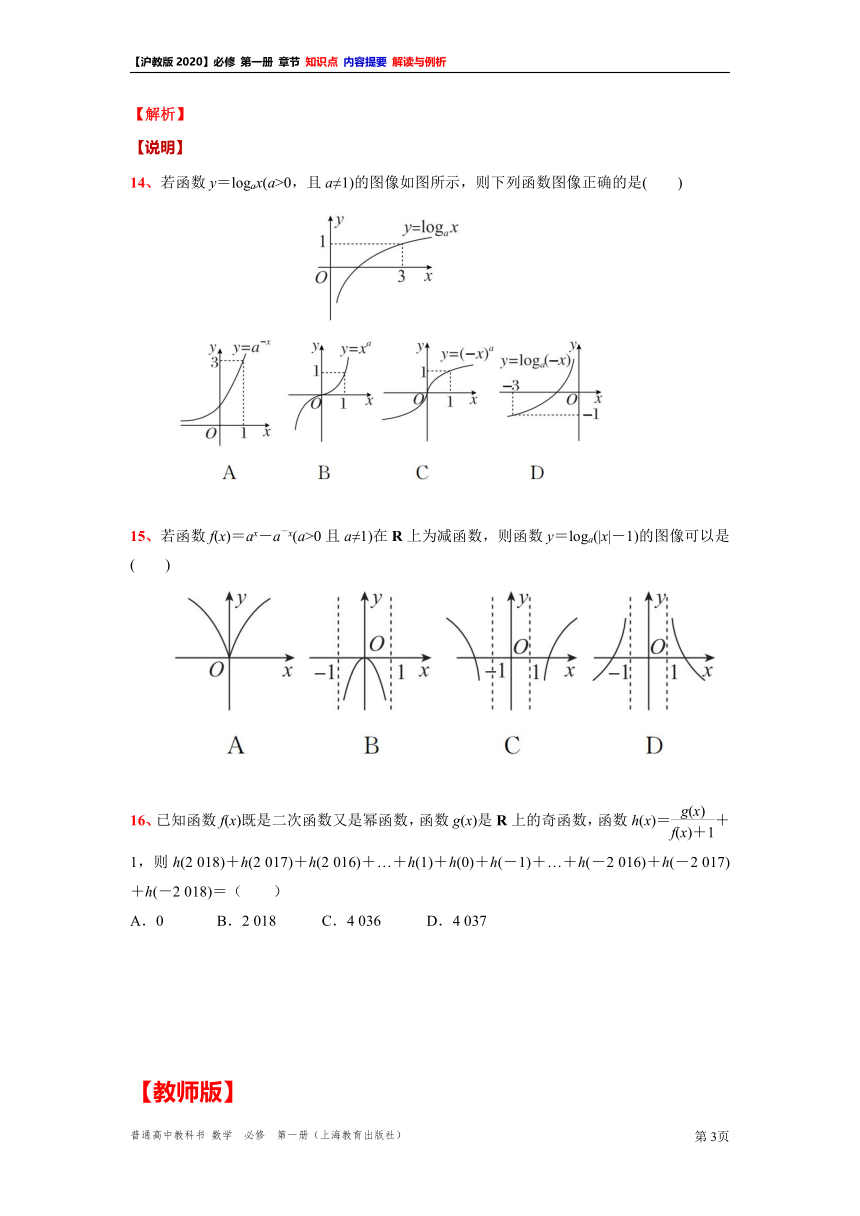
14、若函数y=logax(a>0,且a≠1)的图像如图所示,则下列函数图像正确的是( )
15、若函数f(x)=ax-a-x(a>0且a≠1)在R上为减函数,则函数y=loga(|x|-1)的图像可以是( )
16、已知函数f(x)既是二次函数又是幂函数,函数g(x)是R上的奇函数,函数h(x)=+1,则h(2 018)+h(2 017)+h(2 016)+…+h(1)+h(0)+h(-1)+…+h(-2 016)+h(-2 017)+h(-2 018)=( )
A.0 B.2 018 C.4 036 D.4 037
【教师版】
《第 4 章 幂函数、指数函数与对数函数》填充、选择题测试【3】
一、填空题(本大题共有12题,满分36分)只要求直接填写结果,每个空格填对得3分,
否则一律得零分.
1、若幂函数的图像与坐标轴无公共点,且关于原点对称,则实数m的取值集合为
【提示】注意:幂函数的研究过程与图像特征;
【答案】{0,2};
【解析】由幂函数的图像与坐标轴无公共点,且关于原点对称,
可得m2-2m-3<0(m∈Z),并且m2-2m-3为奇数,解得m=0,或m=2;
则实数m的取值集合为{0,2};
【说明】本题考查了教材上研究幂函数的过程与方法;
2、若函数f(x)=(a>0,a≠1)满足f(1)=,则f(x)的单调递减区间是
【提示】注意:分解复合函数;
【答案】[2,+∞)
【解析】由f(1)=,得a=,因此f(x)=|2x-4|,因为y=|2x-4|在[2,+∞)上单调递增,
所以f(x)的单调递减区间是[2,+∞),
【说明】本题考查了指数函数的定义与复合函数的单调性;
3、已知函数y=f(x)的定义域为(1,2),则函数y=f(2x)的定义域为________
【提示】理解函数的定义域;
【答案】(0,1)
【解析】由函数的定义,得1<2x<2 0<x<1.所以y=f(2x)的定义域为(0,1);
【说明】本题综合考查了函数的定义域、值域;本质是已知“指数函数”的值域求定义域;
4、已知函数f(x)=ax+b的图像过(1,7),其反函数 的图像过点(4,0),则f(x)的表达式为f(x)=
【提示】注意:原函数与反函数间的相互联系;
【答案】4x+3;
【解析】因为,f(x)的反函数图像过点(4,0),所以,f(x)的图像过(0,4),
又f(x)=ax+b的图像过(1,7),所以有方程组
所以,a=4且b=3,故f(x)的表达式为 f(x)=4x+3;
【说明】本题综合考查了原函数与反函数间的代数与图像间联系;
5、若函数f(x)=(a>0,且a≠1)的值域是[4,+∞),则实数a的取值范围是________
【提示】注意:结合分段函数与对应的初等函数性质与图像,求值域;
【答案】(1,2];
【解析】因为f(x)=所以当x≤2时,f(x)≥4;
又函数f(x)的值域为[4,+∞),所以解得1所以实数a的取值范围为(1,2];
【说明】本题主要考查结合函数单调性求值域,与分类讨论进行了交汇;
6、已知函数f(x)=|log2x|,正实数m,n满足m【提示】注意:数形结合地分析;
【答案】;
【解析】根据题意并结合函数f(x)=|log2x|的图像知,0根据函数图像易知,当x=m2时函数f(x)取得最大值,
所以f(m2)=|log2m2|=2,又0【说明】本题主要通过图像变换找出隐含条件,数形结合解之;
7、已知max{a,b}表示a,b两数中的最大值.若f(x)=max{e|x|,e|x-2|},则f(x)的最小值为________
【提示】阅读理解,等价转化;
【答案】e;
【解析】由题意知,f(x)=max{e|x|,e|x-2|}=
当x≥1时,f(x)≥e,且当x=1时,取得最小值e;
当x<1时,f(x)>e,故f(x)的最小值为f(1)=e;
【说明】本题主要通过等价转化为分段函数解之;
8、设函数f(x)=x2-a与g(x)=ax(a>1且a≠2)在区间(0,+∞)上具有不同的单调性,
则M=(a-1)0.2与N=0.1的大小关系是
【提示】注意:挖掘隐含条件;
【答案】M>N;
【解析】因为f(x)=x2-a与g(x)=ax(a>1且a≠2)在区间(0,+∞)上具有不同的单调性;
所以a>2,所以M=(a-1)0.2>1,N=0.1<1,所以M>N;
【说明】本题综合考查了幂函数、指数函数的单调性与利用“1;作为中介量”比较大小;
9、已知函数f(x)=关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是________.
【提示】根据分段函数,结合初等函数解之;
【答案】(1,+∞)
【解析】问题等价于函数y=f(x)与y=-x+a的图像有且只有一个交点,
结合函数图像可知a>1;
【说明】本题考查了初等函数图像与数形结合的交汇;
10、若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围是________
【提示】注意等价转化;
【答案】(0,2);
【解析】在同一平面直角坐标系中画出y=|2x-2|与y=b的图象,如图所示.
所以,当0所以,b的取值范围是(0,2);
【说明】本题主要考查了数形结合的思想;
11、已知函数f(x)=|log2x|,实数a,b满足0【提示】注意:通过图像变换找隐含条件;
【答案】4;
【解析】因为,f(x)=|log2x|,所以,f(x)的图像如图所示,
又f(a)=f(b)且0所以,01且ab=1,所以,a2则a=,即b=2,所以,+b=4.
【说明】本题主要通过对数函数的图像变换,数形结合地挖掘隐含条件;
12、若函数y=|2x-1|在(-∞,m]上单调递减,则m的取值范围是
【提示】注意:数形结合;
【答案】(-∞,0];
【解析】在平面直角坐标系中作出y=2x的图象,把图象沿y轴向下平移1个单位得到y=2x-1的图象,再把y=2x-1的图象在x轴下方的部分关于x轴翻折,其余部分不变.如图,得到y=|2x-1|的图象,由图可知y=|2x-1|在(-∞,0]上单调递减,所以,m∈(-∞,0];
答案:(-∞,0]
【说明】本题主要考查了数形结合思想;
二、选择题(本大题共有4题,满分12分) 每小题都给出四个选项,其中有且只有一个选项是正确的,选对
得 3分,否则一律得零分.
13、在同一直角坐标系中,函数f(x)=xa(x>0),g(x)=logax的图象可能是( )
【提示】注意:通过一个函数确定参数,再通过第2个函数检验;
【答案】D;
【解析】因为a>0,所以f(x)=xa在(0,+∞)上为增函数,故A错.
在B中,由f(x)的图像知a>1,
由g(x)的图像知0在C中,由f(x)的图像知01,矛盾,故C错.
在D中,由f(x)的图像知0由g(x)的图像知0【说明】本题实质还是考了初等函数的图像与性质;
14、若函数y=logax(a>0,且a≠1)的图像如图所示,则下列函数图像正确的是( )
【提示】注意:结合对数函数图像确定参数取值范围;
【答案】B;
【解析】由题图可知y=logax过点(3,1),所以,loga3=1,即a=3.
A项,y=x在R上为减函数,错误;
B项,y=x3符合;
C项,y=-x3在R上为减函数,错误;
D项,y=log3(-x)在(-∞,0)上为减函数,错误.
【说明】本题考查了初等函数的图像与性质;
15、若函数f(x)=ax-a-x(a>0且a≠1)在R上为减函数,则函数y=loga(|x|-1)的图像可以是( )
【提示】注意:初等函数的图像与性质;
【答案】D;
【解析】因函数f(x)=ax-a-x(a>0且a≠1)在R上为减函数,故0易知函数y=loga(|x|-1)是偶函数,定义域为{x|x>1或x<-1},x>1时函数y=loga(|x|-1)的图像可以通过函数y=logax的图像向右平移1个单位得到,故选D;
【说明】本题考查了初等函数的图像与性质与图像变换;
16、已知函数f(x)既是二次函数又是幂函数,函数g(x)是R上的奇函数,函数h(x)=+1,则h(2 018)+h(2 017)+h(2 016)+…+h(1)+h(0)+h(-1)+…+h(-2 016)+h(-2 017)+h(-2 018)=( )
A.0 B.2 018 C.4 036 D.4 037
【提示】注意:初等函数的定义与性质;
【答案】D;
【解析】函数f(x)既是二次函数又是幂函数,所以,f(x)=x2,所以,f(x)+1为R上的偶函数,
又函数g(x)是R上的奇函数,h(x)=+1,
所以,h(x)+h(-x)=+=+2=2,
所以,h(2 018)+h(2 017)+h(2 016)+…+h(1)+h(0)+h(-1)+…+h(-2 016)+h(-2 017)+h(-2 018)
=[h(2 018)+h(-2 018)]+[h(2 017)+h(-2 017)]+…+[h(1)+h(-1)]+h(0)=2+2+…+2+1
=2×2 018+1=4 037;
故选D;
【说明】本题主要考查通过阅读审题,发现自变量的特点,结合函数性质实现“整体”计算;
PAGE
第7页
普通高中教科书 数学 必修 第一册(上海教育出版社)
【学生版】
《第 4 章 幂函数、指数函数与对数函数》填充、选择题测试【3】
一、填空题(本大题共有12题,满分36分)只要求直接填写结果,每个空格填对得3分,
否则一律得零分.
1、若幂函数的图像与坐标轴无公共点,且关于原点对称,则实数m的取值集合为
【提示】
【答案】
【解析】
【说明】
2、若函数f(x)=(a>0,a≠1)满足f(1)=,则f(x)的单调递减区间是
【提示】
【答案】
【解析】
【说明】
3、已知函数y=f(x)的定义域为(1,2),则函数y=f(2x)的定义域为________
【提示】
【答案】
【解析】
【说明】
4、已知函数f(x)=ax+b的图像过(1,7),其反函数 的图像过点(4,0),则f(x)的表达式为f(x)=
【提示】
【答案】
【解析】
【说明】
5、若函数f(x)=(a>0,且a≠1)的值域是[4,+∞),则实数a的取值范围是________
【提示】
【答案】
【解析】
【说明】
6、已知函数f(x)=|log2x|,正实数m,n满足m
8、设函数f(x)=x2-a与g(x)=ax(a>1且a≠2)在区间(0,+∞)上具有不同的单调性,
则M=(a-1)0.2与N=0.1的大小关系是
9、已知函数f(x)=关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是________.
10、若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围是________
11、已知函数f(x)=|log2x|,实数a,b满足0
二、选择题(本大题共有4题,满分12分) 每小题都给出四个选项,其中有且只有一个选项是正确的,选对
得 3分,否则一律得零分.
13、在同一直角坐标系中,函数f(x)=xa(x>0),g(x)=logax的图象可能是( )
【提示】
【答案】
【解析】
【说明】
14、若函数y=logax(a>0,且a≠1)的图像如图所示,则下列函数图像正确的是( )
15、若函数f(x)=ax-a-x(a>0且a≠1)在R上为减函数,则函数y=loga(|x|-1)的图像可以是( )
16、已知函数f(x)既是二次函数又是幂函数,函数g(x)是R上的奇函数,函数h(x)=+1,则h(2 018)+h(2 017)+h(2 016)+…+h(1)+h(0)+h(-1)+…+h(-2 016)+h(-2 017)+h(-2 018)=( )
A.0 B.2 018 C.4 036 D.4 037
【教师版】
《第 4 章 幂函数、指数函数与对数函数》填充、选择题测试【3】
一、填空题(本大题共有12题,满分36分)只要求直接填写结果,每个空格填对得3分,
否则一律得零分.
1、若幂函数的图像与坐标轴无公共点,且关于原点对称,则实数m的取值集合为
【提示】注意:幂函数的研究过程与图像特征;
【答案】{0,2};
【解析】由幂函数的图像与坐标轴无公共点,且关于原点对称,
可得m2-2m-3<0(m∈Z),并且m2-2m-3为奇数,解得m=0,或m=2;
则实数m的取值集合为{0,2};
【说明】本题考查了教材上研究幂函数的过程与方法;
2、若函数f(x)=(a>0,a≠1)满足f(1)=,则f(x)的单调递减区间是
【提示】注意:分解复合函数;
【答案】[2,+∞)
【解析】由f(1)=,得a=,因此f(x)=|2x-4|,因为y=|2x-4|在[2,+∞)上单调递增,
所以f(x)的单调递减区间是[2,+∞),
【说明】本题考查了指数函数的定义与复合函数的单调性;
3、已知函数y=f(x)的定义域为(1,2),则函数y=f(2x)的定义域为________
【提示】理解函数的定义域;
【答案】(0,1)
【解析】由函数的定义,得1<2x<2 0<x<1.所以y=f(2x)的定义域为(0,1);
【说明】本题综合考查了函数的定义域、值域;本质是已知“指数函数”的值域求定义域;
4、已知函数f(x)=ax+b的图像过(1,7),其反函数 的图像过点(4,0),则f(x)的表达式为f(x)=
【提示】注意:原函数与反函数间的相互联系;
【答案】4x+3;
【解析】因为,f(x)的反函数图像过点(4,0),所以,f(x)的图像过(0,4),
又f(x)=ax+b的图像过(1,7),所以有方程组
所以,a=4且b=3,故f(x)的表达式为 f(x)=4x+3;
【说明】本题综合考查了原函数与反函数间的代数与图像间联系;
5、若函数f(x)=(a>0,且a≠1)的值域是[4,+∞),则实数a的取值范围是________
【提示】注意:结合分段函数与对应的初等函数性质与图像,求值域;
【答案】(1,2];
【解析】因为f(x)=所以当x≤2时,f(x)≥4;
又函数f(x)的值域为[4,+∞),所以解得1
【说明】本题主要考查结合函数单调性求值域,与分类讨论进行了交汇;
6、已知函数f(x)=|log2x|,正实数m,n满足m
【答案】;
【解析】根据题意并结合函数f(x)=|log2x|的图像知,0
所以f(m2)=|log2m2|=2,又0
7、已知max{a,b}表示a,b两数中的最大值.若f(x)=max{e|x|,e|x-2|},则f(x)的最小值为________
【提示】阅读理解,等价转化;
【答案】e;
【解析】由题意知,f(x)=max{e|x|,e|x-2|}=
当x≥1时,f(x)≥e,且当x=1时,取得最小值e;
当x<1时,f(x)>e,故f(x)的最小值为f(1)=e;
【说明】本题主要通过等价转化为分段函数解之;
8、设函数f(x)=x2-a与g(x)=ax(a>1且a≠2)在区间(0,+∞)上具有不同的单调性,
则M=(a-1)0.2与N=0.1的大小关系是
【提示】注意:挖掘隐含条件;
【答案】M>N;
【解析】因为f(x)=x2-a与g(x)=ax(a>1且a≠2)在区间(0,+∞)上具有不同的单调性;
所以a>2,所以M=(a-1)0.2>1,N=0.1<1,所以M>N;
【说明】本题综合考查了幂函数、指数函数的单调性与利用“1;作为中介量”比较大小;
9、已知函数f(x)=关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是________.
【提示】根据分段函数,结合初等函数解之;
【答案】(1,+∞)
【解析】问题等价于函数y=f(x)与y=-x+a的图像有且只有一个交点,
结合函数图像可知a>1;
【说明】本题考查了初等函数图像与数形结合的交汇;
10、若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围是________
【提示】注意等价转化;
【答案】(0,2);
【解析】在同一平面直角坐标系中画出y=|2x-2|与y=b的图象,如图所示.
所以,当0
【说明】本题主要考查了数形结合的思想;
11、已知函数f(x)=|log2x|,实数a,b满足0
【答案】4;
【解析】因为,f(x)=|log2x|,所以,f(x)的图像如图所示,
又f(a)=f(b)且0
【说明】本题主要通过对数函数的图像变换,数形结合地挖掘隐含条件;
12、若函数y=|2x-1|在(-∞,m]上单调递减,则m的取值范围是
【提示】注意:数形结合;
【答案】(-∞,0];
【解析】在平面直角坐标系中作出y=2x的图象,把图象沿y轴向下平移1个单位得到y=2x-1的图象,再把y=2x-1的图象在x轴下方的部分关于x轴翻折,其余部分不变.如图,得到y=|2x-1|的图象,由图可知y=|2x-1|在(-∞,0]上单调递减,所以,m∈(-∞,0];
答案:(-∞,0]
【说明】本题主要考查了数形结合思想;
二、选择题(本大题共有4题,满分12分) 每小题都给出四个选项,其中有且只有一个选项是正确的,选对
得 3分,否则一律得零分.
13、在同一直角坐标系中,函数f(x)=xa(x>0),g(x)=logax的图象可能是( )
【提示】注意:通过一个函数确定参数,再通过第2个函数检验;
【答案】D;
【解析】因为a>0,所以f(x)=xa在(0,+∞)上为增函数,故A错.
在B中,由f(x)的图像知a>1,
由g(x)的图像知0
在D中,由f(x)的图像知0
14、若函数y=logax(a>0,且a≠1)的图像如图所示,则下列函数图像正确的是( )
【提示】注意:结合对数函数图像确定参数取值范围;
【答案】B;
【解析】由题图可知y=logax过点(3,1),所以,loga3=1,即a=3.
A项,y=x在R上为减函数,错误;
B项,y=x3符合;
C项,y=-x3在R上为减函数,错误;
D项,y=log3(-x)在(-∞,0)上为减函数,错误.
【说明】本题考查了初等函数的图像与性质;
15、若函数f(x)=ax-a-x(a>0且a≠1)在R上为减函数,则函数y=loga(|x|-1)的图像可以是( )
【提示】注意:初等函数的图像与性质;
【答案】D;
【解析】因函数f(x)=ax-a-x(a>0且a≠1)在R上为减函数,故0
【说明】本题考查了初等函数的图像与性质与图像变换;
16、已知函数f(x)既是二次函数又是幂函数,函数g(x)是R上的奇函数,函数h(x)=+1,则h(2 018)+h(2 017)+h(2 016)+…+h(1)+h(0)+h(-1)+…+h(-2 016)+h(-2 017)+h(-2 018)=( )
A.0 B.2 018 C.4 036 D.4 037
【提示】注意:初等函数的定义与性质;
【答案】D;
【解析】函数f(x)既是二次函数又是幂函数,所以,f(x)=x2,所以,f(x)+1为R上的偶函数,
又函数g(x)是R上的奇函数,h(x)=+1,
所以,h(x)+h(-x)=+=+2=2,
所以,h(2 018)+h(2 017)+h(2 016)+…+h(1)+h(0)+h(-1)+…+h(-2 016)+h(-2 017)+h(-2 018)
=[h(2 018)+h(-2 018)]+[h(2 017)+h(-2 017)]+…+[h(1)+h(-1)]+h(0)=2+2+…+2+1
=2×2 018+1=4 037;
故选D;
【说明】本题主要考查通过阅读审题,发现自变量的特点,结合函数性质实现“整体”计算;
PAGE
第7页
普通高中教科书 数学 必修 第一册(上海教育出版社)
