河北省保定市高阳中学2012-2013学年高二上学期期中考试数学(理)试题
文档属性
| 名称 | 河北省保定市高阳中学2012-2013学年高二上学期期中考试数学(理)试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 232.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-08 00:00:00 | ||
图片预览



文档简介
2012-2013学年第一学期期中考试
高二数学(理科)试卷
(考试时间:120分钟 总分:150分)
一.选择题(本大题共12题,每小题5分,共60分)
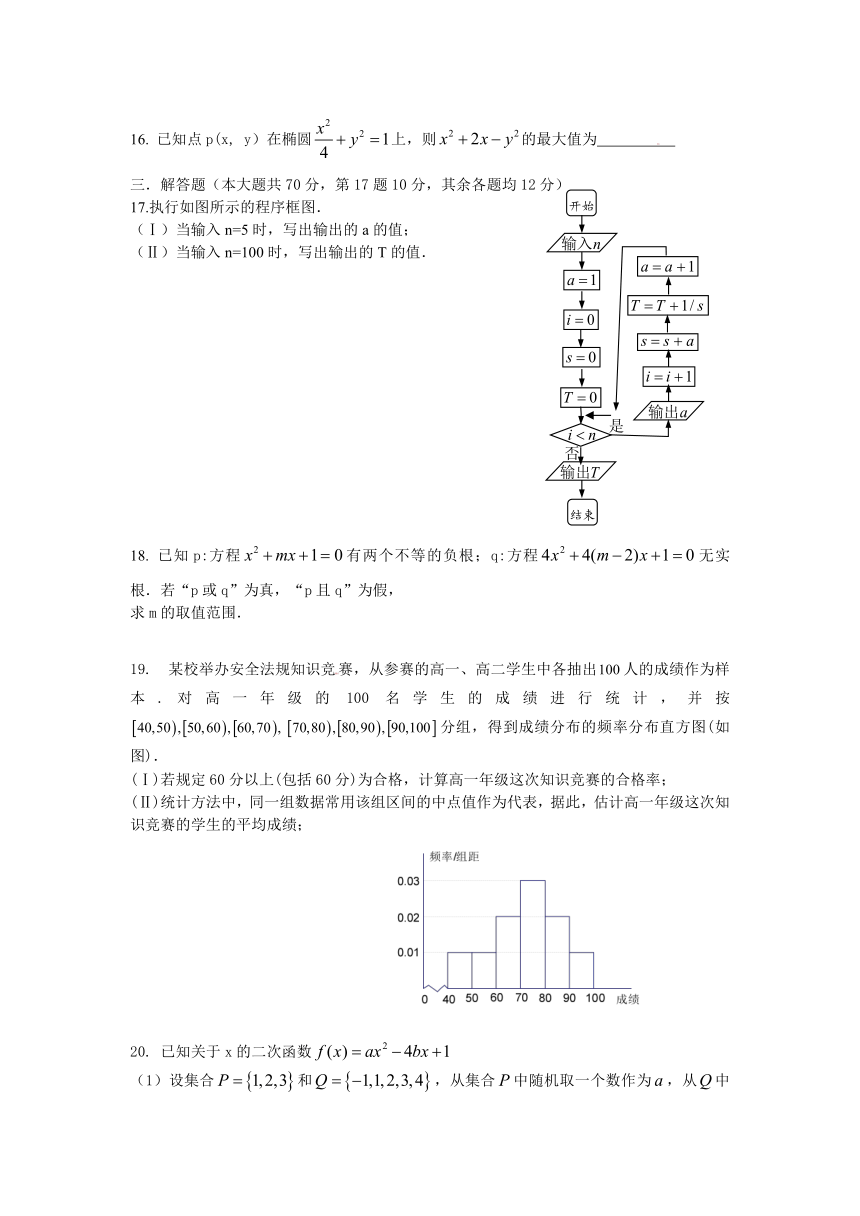
1.如图所示的程序框图输出的结果是( )
A B . C . D .
2.某大学共有本科生5000人,其中一、二、三、四年级的人数比为4∶3∶2∶1,现拟用分层抽样的方法,从所有本科生中抽取一个容量为200的样本,则应从三年级的学生中抽取的人数为( )
A.80 B.40 C.60 D.20
3. 椭圆的焦点坐标是( )
A
B.
C. D.
4.从装有个红球和个黑球的口袋内任取个球,那么互斥而不对立的两个事件是( )
A. 至少有1个黑球与都是黑球
B. 至少有1个红球与都是黑球
C. 至少有1个黑球与至少有个红球
D. 恰有个黑球与恰有个黑球
5.过双曲线x2-=1的右焦点F作直线l交双曲线于A, B两点,若|AB|=4,则这样的
直线l有 ( )A.1条 B.2条 C.3条 D.4条
6. 已知条件p:<2,条件q:-5x-6<0,则p是q的 ( )
A.充分必要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分又不必要条件
7. 直线y=x+3与曲线 =1的交点的个数是( )
A 0个 B 1个 C 2个 D 3个
8. 数据,,,的平均数为,方差为,则数据,,, 的平均数和方差分别是( )
A.和 B.和C.和 D.和
9. 下列结论错误的是 ( )
A.若“p且q”与“”均为假命题,则p真q假.
B.命题“存在”的否定是“对任意”
C.“”是“”的必要不充分条件.
D.“若”的逆命题为真.
10. 已知x与y之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则y与x的线性回归方程为必过定点 ( )
A.(2,2) B.(1,2) C.(1.5,4) D.(1.5,0)
11..连续掷两次骰子,以先后得到的点数m, n为点的坐标,那么点P在圆内部的概率是( )
A. B. C. D.
12.如图,是双曲线上的动点,是双曲线的焦点,是的平分线上的一点,且. 有一同学用以下方法研究:延长交于点,可知为等腰三角形,且为的中点,得. 类似地:是椭圆上的动点,
是椭圆的焦点,是的平分线上的一点,且. 则的取值范围是
A. B. C. D.
二.填空题(本大题共4题,每小题5分,共20分)
13.某班级共有学生54人,现根据学生的学号,用系统抽样的方法,抽取一个容量为4
的样本.已知3号,29号,42号同学在样本中,那么样本中还有一个同学的学号是
14.用秦九韶算法求多项式 ,当时,的值为
15. 甲乙两人玩猜数字游戏,先由甲在心中任想一个数字,记为,再由乙猜甲刚才所想的数字,把乙猜的数字记为,且。若,则称甲乙“心有灵犀”。现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 。
16. 已知点p(x, y)在椭圆上,则的最大值为
三.解答题(本大题共70分,第17题10分,其余各题均12分)
17.执行如图所示的程序框图.
(Ⅰ)当输入n=5时,写出输出的a的值;
(Ⅱ)当输入n=100时,写出输出的T的值.
18. 已知p:方程有两个不等的负根;q:方程无实根.若“p或q”为真,“p且q”为假,
求m的取值范围.
19. 某校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出人的成绩作为样本.对高一年级的100名学生的成绩进行统计,并按分组,得到成绩分布的频率分布直方图(如图).
(Ⅰ)若规定60分以上(包括60分)为合格,计算高一年级这次知识竞赛的合格率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;
20. 已知关于x的二次函数
(1)设集合和,从集合中随机取一个数作为,从中随机取一个数作为,求函数在区间上是增函数的概率;
(2)设点是区域内的随机点,求函数在区间上是增函数的概率。
21.在平面直角坐标系中,点P到两点,的距离之和等于4,设点P的轨迹为.
(Ⅰ)写出C的方程;
(Ⅱ)设直线与C交于A,B两点.k为何值时?此时的值是多少?
22.已知中心在原点的双曲线C的一个焦点是F1(,0),一条渐近线方程为:
(1)求双曲线C的标准方程;
(2)若以为斜率的直线与双曲线C相交于两个不同的点M、N,且线段
MN的垂直平分线与两坐标轴围成的三角形的面积为,求的取值范围。
2012-2013学年第一学期期中考试
高二数学(理科)试卷答案
一.选择题
1-5 CBBDC 6-10 BDCCC 11-12 AD
二.填空题
13.16 14.262 15. 16.
三.解答题
17. 解 (Ⅰ)输出的a分别是:1,2,3,4,5;-------------------5分
(Ⅱ)------7分
--------------------------------------10分
故输出的T的值为 18. 解:由已知可得
----------------4分
即: --------------6分
∵“p或q”为真,“p且q”为假,则p与 q中有一真一假 ---7分
(1)当p真q假时 有
得 -----------------9分
(2)当p假q真时 有
得 --------------11分
综上所求m的取值范围为: ---------12分
19. 解:
(Ⅰ)高一合格率为=80﹪; ……6分
(Ⅱ)高一样本的平均数
,
据此,可以估计高一年级这次知识竞赛的学生的平均成绩为72分. ………12分
20. 解(1)∵函数的图象的对称轴为
要使在区间上为增函数,
当且仅当>0且……………………2分
若=1则=-1,
若=2则=-1,1
若=3则=-1,1,;………………4分
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为………………6分
(2)由(1)知当且仅当且>0时,
函数在区间上为增函数,
依条件可知试验的全部结果所构成的区域为
构成所求事件的区域为三角形部分。………………9分
由………
∴所求事件的概率为………………12分
21.(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以为焦点,长半轴为2的椭圆.它的短半轴,
故曲线C的方程为.………………………………………………4分
(Ⅱ)设,其坐标满足
消去y并整理得, 显然△>0
故.…………………………………………6分
,即. 而,
于是.
所以时,,故.…………………………8分
当时,,.
,
而,
所以. ………………………………………………………12分
22.
高二数学(理科)试卷
(考试时间:120分钟 总分:150分)
一.选择题(本大题共12题,每小题5分,共60分)
1.如图所示的程序框图输出的结果是( )
A B . C . D .
2.某大学共有本科生5000人,其中一、二、三、四年级的人数比为4∶3∶2∶1,现拟用分层抽样的方法,从所有本科生中抽取一个容量为200的样本,则应从三年级的学生中抽取的人数为( )
A.80 B.40 C.60 D.20
3. 椭圆的焦点坐标是( )
A
B.
C. D.
4.从装有个红球和个黑球的口袋内任取个球,那么互斥而不对立的两个事件是( )
A. 至少有1个黑球与都是黑球
B. 至少有1个红球与都是黑球
C. 至少有1个黑球与至少有个红球
D. 恰有个黑球与恰有个黑球
5.过双曲线x2-=1的右焦点F作直线l交双曲线于A, B两点,若|AB|=4,则这样的
直线l有 ( )A.1条 B.2条 C.3条 D.4条
6. 已知条件p:<2,条件q:-5x-6<0,则p是q的 ( )
A.充分必要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分又不必要条件
7. 直线y=x+3与曲线 =1的交点的个数是( )
A 0个 B 1个 C 2个 D 3个
8. 数据,,,的平均数为,方差为,则数据,,, 的平均数和方差分别是( )
A.和 B.和C.和 D.和
9. 下列结论错误的是 ( )
A.若“p且q”与“”均为假命题,则p真q假.
B.命题“存在”的否定是“对任意”
C.“”是“”的必要不充分条件.
D.“若”的逆命题为真.
10. 已知x与y之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则y与x的线性回归方程为必过定点 ( )
A.(2,2) B.(1,2) C.(1.5,4) D.(1.5,0)
11..连续掷两次骰子,以先后得到的点数m, n为点的坐标,那么点P在圆内部的概率是( )
A. B. C. D.
12.如图,是双曲线上的动点,是双曲线的焦点,是的平分线上的一点,且. 有一同学用以下方法研究:延长交于点,可知为等腰三角形,且为的中点,得. 类似地:是椭圆上的动点,
是椭圆的焦点,是的平分线上的一点,且. 则的取值范围是
A. B. C. D.
二.填空题(本大题共4题,每小题5分,共20分)
13.某班级共有学生54人,现根据学生的学号,用系统抽样的方法,抽取一个容量为4
的样本.已知3号,29号,42号同学在样本中,那么样本中还有一个同学的学号是
14.用秦九韶算法求多项式 ,当时,的值为
15. 甲乙两人玩猜数字游戏,先由甲在心中任想一个数字,记为,再由乙猜甲刚才所想的数字,把乙猜的数字记为,且。若,则称甲乙“心有灵犀”。现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 。
16. 已知点p(x, y)在椭圆上,则的最大值为
三.解答题(本大题共70分,第17题10分,其余各题均12分)
17.执行如图所示的程序框图.
(Ⅰ)当输入n=5时,写出输出的a的值;
(Ⅱ)当输入n=100时,写出输出的T的值.
18. 已知p:方程有两个不等的负根;q:方程无实根.若“p或q”为真,“p且q”为假,
求m的取值范围.
19. 某校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出人的成绩作为样本.对高一年级的100名学生的成绩进行统计,并按分组,得到成绩分布的频率分布直方图(如图).
(Ⅰ)若规定60分以上(包括60分)为合格,计算高一年级这次知识竞赛的合格率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;
20. 已知关于x的二次函数
(1)设集合和,从集合中随机取一个数作为,从中随机取一个数作为,求函数在区间上是增函数的概率;
(2)设点是区域内的随机点,求函数在区间上是增函数的概率。
21.在平面直角坐标系中,点P到两点,的距离之和等于4,设点P的轨迹为.
(Ⅰ)写出C的方程;
(Ⅱ)设直线与C交于A,B两点.k为何值时?此时的值是多少?
22.已知中心在原点的双曲线C的一个焦点是F1(,0),一条渐近线方程为:
(1)求双曲线C的标准方程;
(2)若以为斜率的直线与双曲线C相交于两个不同的点M、N,且线段
MN的垂直平分线与两坐标轴围成的三角形的面积为,求的取值范围。
2012-2013学年第一学期期中考试
高二数学(理科)试卷答案
一.选择题
1-5 CBBDC 6-10 BDCCC 11-12 AD
二.填空题
13.16 14.262 15. 16.
三.解答题
17. 解 (Ⅰ)输出的a分别是:1,2,3,4,5;-------------------5分
(Ⅱ)------7分
--------------------------------------10分
故输出的T的值为 18. 解:由已知可得
----------------4分
即: --------------6分
∵“p或q”为真,“p且q”为假,则p与 q中有一真一假 ---7分
(1)当p真q假时 有
得 -----------------9分
(2)当p假q真时 有
得 --------------11分
综上所求m的取值范围为: ---------12分
19. 解:
(Ⅰ)高一合格率为=80﹪; ……6分
(Ⅱ)高一样本的平均数
,
据此,可以估计高一年级这次知识竞赛的学生的平均成绩为72分. ………12分
20. 解(1)∵函数的图象的对称轴为
要使在区间上为增函数,
当且仅当>0且……………………2分
若=1则=-1,
若=2则=-1,1
若=3则=-1,1,;………………4分
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为………………6分
(2)由(1)知当且仅当且>0时,
函数在区间上为增函数,
依条件可知试验的全部结果所构成的区域为
构成所求事件的区域为三角形部分。………………9分
由………
∴所求事件的概率为………………12分
21.(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以为焦点,长半轴为2的椭圆.它的短半轴,
故曲线C的方程为.………………………………………………4分
(Ⅱ)设,其坐标满足
消去y并整理得, 显然△>0
故.…………………………………………6分
,即. 而,
于是.
所以时,,故.…………………………8分
当时,,.
,
而,
所以. ………………………………………………………12分
22.
同课章节目录
