人教版七年级数学上册第三章 一元一次方程小结与复习优秀公开课课件(共21张PPT)
文档属性
| 名称 | 人教版七年级数学上册第三章 一元一次方程小结与复习优秀公开课课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 642.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 19:34:42 | ||
图片预览








文档简介
(共21张PPT)
第三章 一元一次方程 小结与复习
人教版 数学 七年级 上册
学习目标
通过对本章知识点的梳理和复习,能理解一元一次方程概念和 等式性质,能熟练地解一元一次方程及实际应用。全面提高学生分 析问题、解决问题的能力。
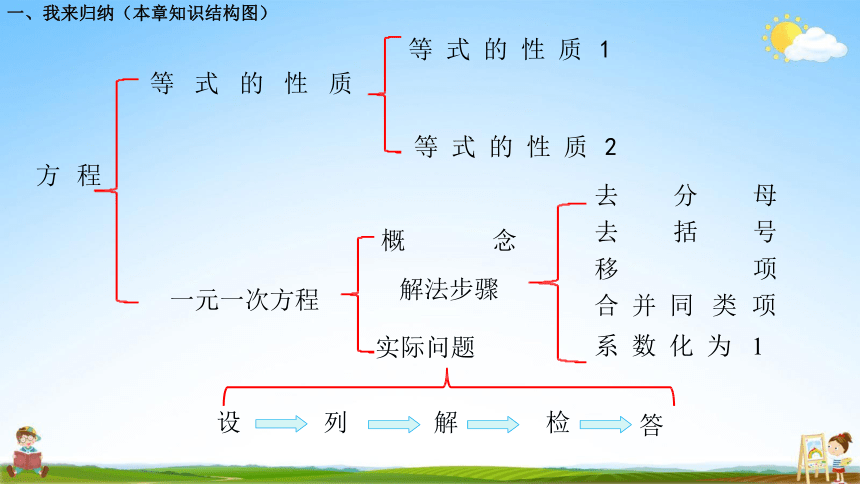
一、我来归纳(本章知识结构图)
实际问题
去 去 移
分 括
母 号 项
概 念
解法步骤
一元一次方程
方 程
等 式 的 性 质 1
等 式 的 性 质
等 式 的 性 质 2
设
列
解
检
合 并 同 类 项 系 数 化 为 1
答
二、重点知识梳理
(一)相关概念
方程:含有未知数的等式叫做方程.
一元一次方程的概念:只含有 一 个未知数,未 知数的次数都是 1 ,等号两边都是 整式 ,这 样的方程叫做一元一次方程.
方程的解:使方程左右两边的值相等的未知数的 值叫做方程的解.
解方程:求方程解的过程叫做解方程.
等.如果 a=b,那么 a± =b±c.
= .
3、等式的对称性:调换等式的两边的位置,等式仍相等。如果a=b那 么b=a
(二)等式的性质
1. 等式的性质1:等式两边加 (或减) 同一个数 (或式子),结果仍相
2. 等式的性质2:等式两边乘同一个数,或除以同一个不为 0 的数, 结果仍相等.如果 a=b,那么 ac= bc ;如果 a = b (c≠0),那么
c
a
c
b
c
(三)、解一元一次方程的一般步骤:
去分母:方程两边都乘各分母的最小公倍数,别漏乘.
去括号:注意括号前的系数与符号.
移项:把含有未知数的项移到方程的左边,常数项移到方程右边, 移项注意要改变符号.
合并同类项:把方程化成 ax = b (a≠0)的形式.
系数化为1:方程两边同除以 x 的系数,得x=m 的形式.
注意:上面仅说明了解一元一次方程常用到的几个步骤,但并不是 说解每一个方程都必须经过这五个步骤。解一元一次方程时,一定 要先认真观察方程的形式,再选择步骤和方法。
设:设未知数,设其中某个未知量为x. 列:根据题意寻找等量关系列方程. 解:解方程.
验:检验方程的解是否符合题意. 答:写出答案 (包括单位).
(四)、列方程解实际问题的一般步骤及注意事项
1. 列方程解决实际问题的一般步骤:
审:审清题意,分清题中的已知量、未知量.
审题是基础,找等量关 系是关键.
解题过程要书写出来的步骤是设、列、解、答。
常见的几种方程类型及等量关系:
行程问题中基本量之间关系: 路程=速度×时间.
① 相遇问题:
全路程=甲走的路程+乙走的路程;
② 追及问题:
甲为快者,被追路程=甲走路程-乙走路程;
③ 流水行船问题:
v顺=v静+v水,v逆=v静-v水.
(2) 工程问题中基本量之间的关系:
① 工作量 = 工作效率×工作时间;
② 合作的工作效率 = 工作效率之和;
③ 工作总量 = 各部分工作量之和 = 合作的工作效率×工作时间;
④ 在没有具体数值的情况下,通常把工作总量看做1.
(3) 销售问题中基本量之间的关系:
① 商品利润 = 商品售价-商品进价;
商品利润
② 利润率 = 100%;
③ 商品售价 = 标价×
;
10
商品进价
折扣数
④ 商品售价 = 商品进价+商品利润
= 商品进价+商品进价×利润率
= 商品进价×(1+利润率).
学习探究
一、小组交流(交流前面学习中遗忘或者有困难的知识点及方法)
二、基础演练
X-1=
1
x
1、下列方程中,是一元一次方程的是( B) A. X -4x=3 B. X=0 C.x+2y=1 D.
2、方程2x+a-4=0的解是x=-2,则a等于( D )
A. 3a-5=2b B. 3a+1=2b+6
2
C. 3ac=2bc+5 D. a=
3
5
b+
3
A. -8 B. 0 C. 2 D. 8
3、已知等式3a=2b+5,则下列等式中不一定成立的是( C )
1-x+3=3x
x-3
6
B. 6-x-3=3x C. 6-x+3=3x D.
4、解方程 1-
A. 1-x-3=3x
x
= 2
,去分母,正确的是( B )
某商品提价100%后要恢复原价,则应降价( B )
A. 30 % B. 50 % C. 75 % D.100 %
鸡兔同笼共9只,腿26条,则鸡有 5 只,兔有 4 只
7、当x= 1 时,代数式4x+2与3x-9的值互为相反数
(3)
8、 解下列方程:
(1) 2 x 1 1 x 10 x 1
4 12
2
4
(2) 4 3 2
3 4 1 x 1 8 3 x
x 2 2 x 3 .
5 2
去括号,得 移项,得
3(2x+1)-12 = 12x-(10x+1).
6x+3-12 = 12x-10x-1.
6x-12x+10x = -1-3+12.
合并同类项,得 系数化为1,得
4x = 8.
x = 2.
4 12
去分母,得
解: 2 x 1 1 x 10 x 1
提示:先用分配律、去括号简化方程,再求解较容易.
(2)
2
4
4 3 2
3 4 1 x 1 8. 3 x
解:去括号,得
1 x 1 6 3 x .
2 4 2
移项,得
1 x 3 x 1 6 .
2 2 4
合并同类项,得
x 6 1 .
系数化为1,得
4
4
x 6 1 .
解:
x 2 2 x 3 .
5 2
去分母,得 2(x-2) = 20-5(x+3).
去括号,得 移项,得
2x-4 = 20-5x-15.
2x+5x = 20-15+4.
合并同类项,得 7x = 9.
系数化为1,得 x 9 .
7
9. “十一”期间,甲、乙两商场有某品牌服装共450件,由于甲 商场销量上升,需从乙商场调运该服装50件,调运后甲商场该服 装的数量是乙商场的2倍,求甲、乙两商场原来各自有该品牌服 装的数量.
解:设甲商城原来有该品牌服装x件,则乙商城原来有该品牌服 装(450-x)件,
根据题意,得x+50=2[(450-x)-50], 解得x=250,则450-x=200.
答:甲商城原来有该品牌服装250件,乙商城原来有该品牌服装
200件.
为鼓励居民节约用电,某地对居民用户用电收费标 准作如下规定:每户每月用电如果不超过 100 度, 那么每度按 0.50 元收费;如果超过 100 度不超过 200 度,那么超过的部分每度按 0.65 元收费;如果 超过200度,那么超过的部分每度按 0.75 元收费.
若居民甲在 6 月份用电 100 度,则 他这个月应缴纳电费 50 元;
若居民乙在 7 月份用电 200 度,则他这个月应缴
纳电费 115 元;
若居民丙在 8 月份用电 300 度,则他这个月应缴
纳电费 190 元;
(2) 若某户居民在9月份缴纳电费310元,那么他这个 月用电多少度?
解:设他这个月用电 x 度,根据题意得:
0.50×100+0.65×(200-100)+0.75×(x-200) = 310,
解得 x = 460.
答:他这个月用电 460 度.
谢谢观看
Thank You
第三章 一元一次方程 小结与复习
人教版 数学 七年级 上册
学习目标
通过对本章知识点的梳理和复习,能理解一元一次方程概念和 等式性质,能熟练地解一元一次方程及实际应用。全面提高学生分 析问题、解决问题的能力。
一、我来归纳(本章知识结构图)
实际问题
去 去 移
分 括
母 号 项
概 念
解法步骤
一元一次方程
方 程
等 式 的 性 质 1
等 式 的 性 质
等 式 的 性 质 2
设
列
解
检
合 并 同 类 项 系 数 化 为 1
答
二、重点知识梳理
(一)相关概念
方程:含有未知数的等式叫做方程.
一元一次方程的概念:只含有 一 个未知数,未 知数的次数都是 1 ,等号两边都是 整式 ,这 样的方程叫做一元一次方程.
方程的解:使方程左右两边的值相等的未知数的 值叫做方程的解.
解方程:求方程解的过程叫做解方程.
等.如果 a=b,那么 a± =b±c.
= .
3、等式的对称性:调换等式的两边的位置,等式仍相等。如果a=b那 么b=a
(二)等式的性质
1. 等式的性质1:等式两边加 (或减) 同一个数 (或式子),结果仍相
2. 等式的性质2:等式两边乘同一个数,或除以同一个不为 0 的数, 结果仍相等.如果 a=b,那么 ac= bc ;如果 a = b (c≠0),那么
c
a
c
b
c
(三)、解一元一次方程的一般步骤:
去分母:方程两边都乘各分母的最小公倍数,别漏乘.
去括号:注意括号前的系数与符号.
移项:把含有未知数的项移到方程的左边,常数项移到方程右边, 移项注意要改变符号.
合并同类项:把方程化成 ax = b (a≠0)的形式.
系数化为1:方程两边同除以 x 的系数,得x=m 的形式.
注意:上面仅说明了解一元一次方程常用到的几个步骤,但并不是 说解每一个方程都必须经过这五个步骤。解一元一次方程时,一定 要先认真观察方程的形式,再选择步骤和方法。
设:设未知数,设其中某个未知量为x. 列:根据题意寻找等量关系列方程. 解:解方程.
验:检验方程的解是否符合题意. 答:写出答案 (包括单位).
(四)、列方程解实际问题的一般步骤及注意事项
1. 列方程解决实际问题的一般步骤:
审:审清题意,分清题中的已知量、未知量.
审题是基础,找等量关 系是关键.
解题过程要书写出来的步骤是设、列、解、答。
常见的几种方程类型及等量关系:
行程问题中基本量之间关系: 路程=速度×时间.
① 相遇问题:
全路程=甲走的路程+乙走的路程;
② 追及问题:
甲为快者,被追路程=甲走路程-乙走路程;
③ 流水行船问题:
v顺=v静+v水,v逆=v静-v水.
(2) 工程问题中基本量之间的关系:
① 工作量 = 工作效率×工作时间;
② 合作的工作效率 = 工作效率之和;
③ 工作总量 = 各部分工作量之和 = 合作的工作效率×工作时间;
④ 在没有具体数值的情况下,通常把工作总量看做1.
(3) 销售问题中基本量之间的关系:
① 商品利润 = 商品售价-商品进价;
商品利润
② 利润率 = 100%;
③ 商品售价 = 标价×
;
10
商品进价
折扣数
④ 商品售价 = 商品进价+商品利润
= 商品进价+商品进价×利润率
= 商品进价×(1+利润率).
学习探究
一、小组交流(交流前面学习中遗忘或者有困难的知识点及方法)
二、基础演练
X-1=
1
x
1、下列方程中,是一元一次方程的是( B) A. X -4x=3 B. X=0 C.x+2y=1 D.
2、方程2x+a-4=0的解是x=-2,则a等于( D )
A. 3a-5=2b B. 3a+1=2b+6
2
C. 3ac=2bc+5 D. a=
3
5
b+
3
A. -8 B. 0 C. 2 D. 8
3、已知等式3a=2b+5,则下列等式中不一定成立的是( C )
1-x+3=3x
x-3
6
B. 6-x-3=3x C. 6-x+3=3x D.
4、解方程 1-
A. 1-x-3=3x
x
= 2
,去分母,正确的是( B )
某商品提价100%后要恢复原价,则应降价( B )
A. 30 % B. 50 % C. 75 % D.100 %
鸡兔同笼共9只,腿26条,则鸡有 5 只,兔有 4 只
7、当x= 1 时,代数式4x+2与3x-9的值互为相反数
(3)
8、 解下列方程:
(1) 2 x 1 1 x 10 x 1
4 12
2
4
(2) 4 3 2
3 4 1 x 1 8 3 x
x 2 2 x 3 .
5 2
去括号,得 移项,得
3(2x+1)-12 = 12x-(10x+1).
6x+3-12 = 12x-10x-1.
6x-12x+10x = -1-3+12.
合并同类项,得 系数化为1,得
4x = 8.
x = 2.
4 12
去分母,得
解: 2 x 1 1 x 10 x 1
提示:先用分配律、去括号简化方程,再求解较容易.
(2)
2
4
4 3 2
3 4 1 x 1 8. 3 x
解:去括号,得
1 x 1 6 3 x .
2 4 2
移项,得
1 x 3 x 1 6 .
2 2 4
合并同类项,得
x 6 1 .
系数化为1,得
4
4
x 6 1 .
解:
x 2 2 x 3 .
5 2
去分母,得 2(x-2) = 20-5(x+3).
去括号,得 移项,得
2x-4 = 20-5x-15.
2x+5x = 20-15+4.
合并同类项,得 7x = 9.
系数化为1,得 x 9 .
7
9. “十一”期间,甲、乙两商场有某品牌服装共450件,由于甲 商场销量上升,需从乙商场调运该服装50件,调运后甲商场该服 装的数量是乙商场的2倍,求甲、乙两商场原来各自有该品牌服 装的数量.
解:设甲商城原来有该品牌服装x件,则乙商城原来有该品牌服 装(450-x)件,
根据题意,得x+50=2[(450-x)-50], 解得x=250,则450-x=200.
答:甲商城原来有该品牌服装250件,乙商城原来有该品牌服装
200件.
为鼓励居民节约用电,某地对居民用户用电收费标 准作如下规定:每户每月用电如果不超过 100 度, 那么每度按 0.50 元收费;如果超过 100 度不超过 200 度,那么超过的部分每度按 0.65 元收费;如果 超过200度,那么超过的部分每度按 0.75 元收费.
若居民甲在 6 月份用电 100 度,则 他这个月应缴纳电费 50 元;
若居民乙在 7 月份用电 200 度,则他这个月应缴
纳电费 115 元;
若居民丙在 8 月份用电 300 度,则他这个月应缴
纳电费 190 元;
(2) 若某户居民在9月份缴纳电费310元,那么他这个 月用电多少度?
解:设他这个月用电 x 度,根据题意得:
0.50×100+0.65×(200-100)+0.75×(x-200) = 310,
解得 x = 460.
答:他这个月用电 460 度.
谢谢观看
Thank You
