北师大版九年级数学上册第4章图形的相似回顾与思考课件(共16张PPT)
文档属性
| 名称 | 北师大版九年级数学上册第4章图形的相似回顾与思考课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 19:49:40 | ||
图片预览



文档简介
(共16张PPT)
第四章 图形的相似
回顾与思考
一、展现自我
回顾本章所学的知识
1、四条线段a、b、c、d成比例,其中b=3cm,c=2cm,d=6cm,求线段a的长。
二、巩固提升:
2、如果两个相似多边形面积的比为4︰9,那么这两个相似多边形对应边的比是多少?
做一做:
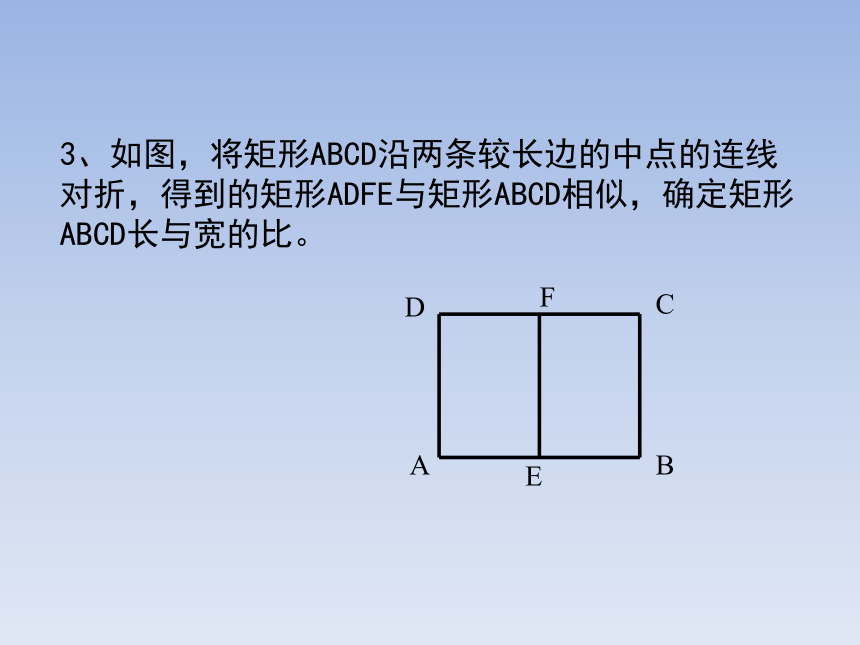
3、如图,将矩形ABCD沿两条较长边的中点的连线对折,得到的矩形ADFE与矩形ABCD相似,确定矩形ABCD长与宽的比。
A
B
C
D
E
F
A
B
O
C
D
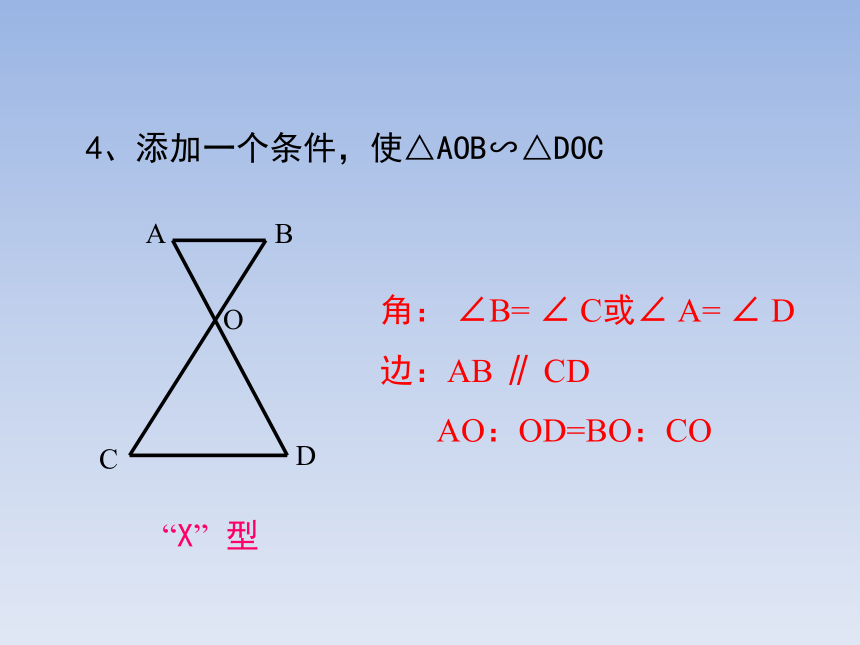
4、添加一个条件,使△AOB∽△DOC
角: ∠B= ∠ C或∠ A= ∠ D
边:AB ∥ CD
AO:OD=BO:CO
“X” 型
A
B
C
D
E
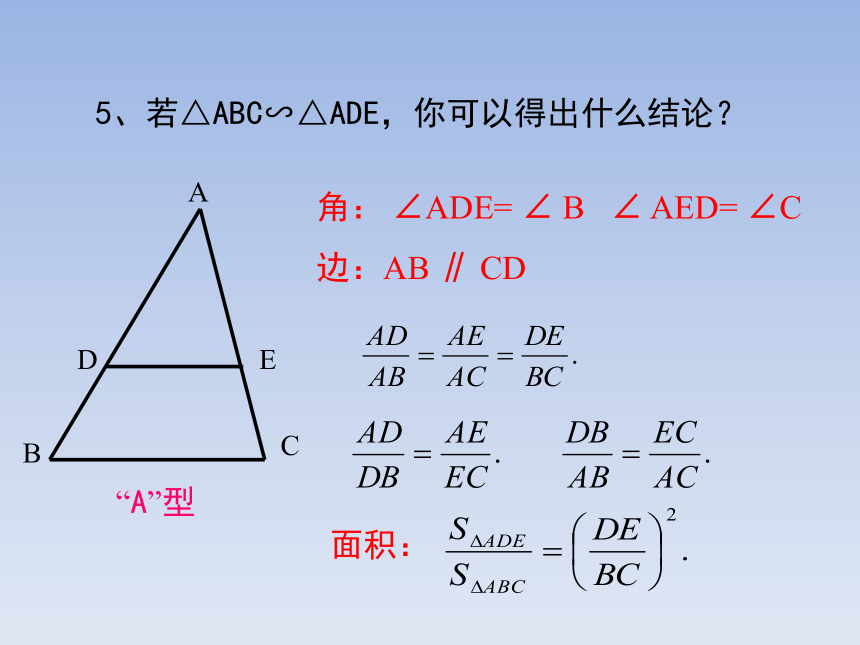
5、若△ABC∽△ADE,你可以得出什么结论?
角: ∠ADE= ∠ B ∠ AED= ∠C
边:AB ∥ CD
面积:
“A”型
A
B
C
D
E
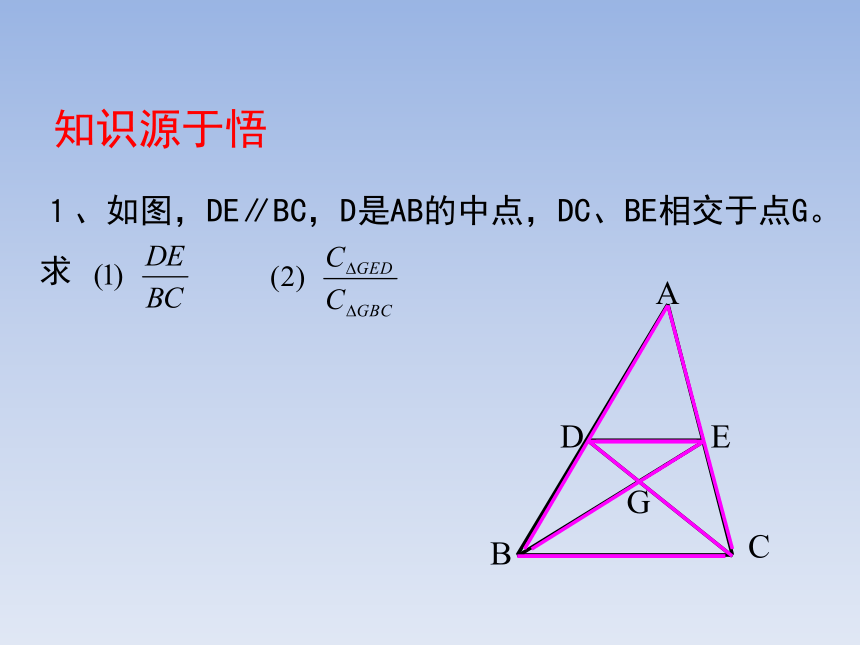
1、如图,DE∥BC,D是AB的中点,DC、BE相交于点G。
求
G
知识源于悟
A
B
C
D
E
F
2、如图: DE∥BC,EF ∥AB,AE:EC=2:3,S△ABC=25,求S四边形BDEF
1、在正方形方格中, △ABC的顶点A、B、C在单位正方形的顶点上 ,请在图中画一个△A1B1C1使△A1B1C1∽△ABC(相似比不为1),且点都在单位正方形的顶点上 .
C
A
B
试一试:
2、动手操作一下
两块完全相同的等腰三角形放成如图样子,假设图形中的所有点、线、面都在同一平面内,则图中有相似(不包括全等)三角形吗?如果有,就把它们一一写出来。
3、如图,BC与EF在一条直线上,AC//DF。将图(2)中的三角形截去一块,使它变为与图(1)相似的图形。
A
B
C
D
E
F
A
B
C
D
E
F
G
P
Q
A
E
B
F
D
C
1、如图,在 ABCD中,E是BC上一点, BE:EC=1:2,AE与BD相交于F,则BF:FD=_______,S△ADF:S△EBF =______
1:3
1:9
三、课堂反馈:
2、如图,能保证使△ACD与△ABC相似的
条件是( )
C
A
B
D
(1)AC︰CD = AB︰BC
(2)CD︰AD = BC︰AC
(3)AC = AD · AB
2
(4)CD = AD · AB
2
C
3、如图,在△ABC中,已知DE//BC,AD=3BD,
S
△ABC
=48,求
S
△ADE
A
B
C
D
E
如图,在△ABC中,∠BAC=90°,AB=6,BC=12,点P从A点出发向B以1m/s的速度移动,点Q从B点出发向C点以2m/s的速度移动,如果P、Q分别从A、B两地同时出发,几秒后△PBQ与原三角形相似?
A
B
C
Q
P
Q
P
选做:
四、小结:
本节课你有什么收获?
第四章 图形的相似
回顾与思考
一、展现自我
回顾本章所学的知识
1、四条线段a、b、c、d成比例,其中b=3cm,c=2cm,d=6cm,求线段a的长。
二、巩固提升:
2、如果两个相似多边形面积的比为4︰9,那么这两个相似多边形对应边的比是多少?
做一做:
3、如图,将矩形ABCD沿两条较长边的中点的连线对折,得到的矩形ADFE与矩形ABCD相似,确定矩形ABCD长与宽的比。
A
B
C
D
E
F
A
B
O
C
D
4、添加一个条件,使△AOB∽△DOC
角: ∠B= ∠ C或∠ A= ∠ D
边:AB ∥ CD
AO:OD=BO:CO
“X” 型
A
B
C
D
E
5、若△ABC∽△ADE,你可以得出什么结论?
角: ∠ADE= ∠ B ∠ AED= ∠C
边:AB ∥ CD
面积:
“A”型
A
B
C
D
E
1、如图,DE∥BC,D是AB的中点,DC、BE相交于点G。
求
G
知识源于悟
A
B
C
D
E
F
2、如图: DE∥BC,EF ∥AB,AE:EC=2:3,S△ABC=25,求S四边形BDEF
1、在正方形方格中, △ABC的顶点A、B、C在单位正方形的顶点上 ,请在图中画一个△A1B1C1使△A1B1C1∽△ABC(相似比不为1),且点都在单位正方形的顶点上 .
C
A
B
试一试:
2、动手操作一下
两块完全相同的等腰三角形放成如图样子,假设图形中的所有点、线、面都在同一平面内,则图中有相似(不包括全等)三角形吗?如果有,就把它们一一写出来。
3、如图,BC与EF在一条直线上,AC//DF。将图(2)中的三角形截去一块,使它变为与图(1)相似的图形。
A
B
C
D
E
F
A
B
C
D
E
F
G
P
Q
A
E
B
F
D
C
1、如图,在 ABCD中,E是BC上一点, BE:EC=1:2,AE与BD相交于F,则BF:FD=_______,S△ADF:S△EBF =______
1:3
1:9
三、课堂反馈:
2、如图,能保证使△ACD与△ABC相似的
条件是( )
C
A
B
D
(1)AC︰CD = AB︰BC
(2)CD︰AD = BC︰AC
(3)AC = AD · AB
2
(4)CD = AD · AB
2
C
3、如图,在△ABC中,已知DE//BC,AD=3BD,
S
△ABC
=48,求
S
△ADE
A
B
C
D
E
如图,在△ABC中,∠BAC=90°,AB=6,BC=12,点P从A点出发向B以1m/s的速度移动,点Q从B点出发向C点以2m/s的速度移动,如果P、Q分别从A、B两地同时出发,几秒后△PBQ与原三角形相似?
A
B
C
Q
P
Q
P
选做:
四、小结:
本节课你有什么收获?
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
