5.3.1函数的单调性(共20张PPT)
文档属性
| 名称 | 5.3.1函数的单调性(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 09:09:08 | ||
图片预览






文档简介
(共20张PPT)
5.3.1
函数的单调性
选择性必修 第二册 第五章 一元函数的导数及其应用
学习目标
1.结合实例,直观探索并掌握函数的单调性与
导数的关系;
2.能利用导数研究函数的单调性,明确导数与函数单调性的关系;
3.会求次数不超过三次的函数的单调区间
4.核心素养:直观想象、数学抽象、数学运算。
y
x
o
a
b
y
x
o
a
b
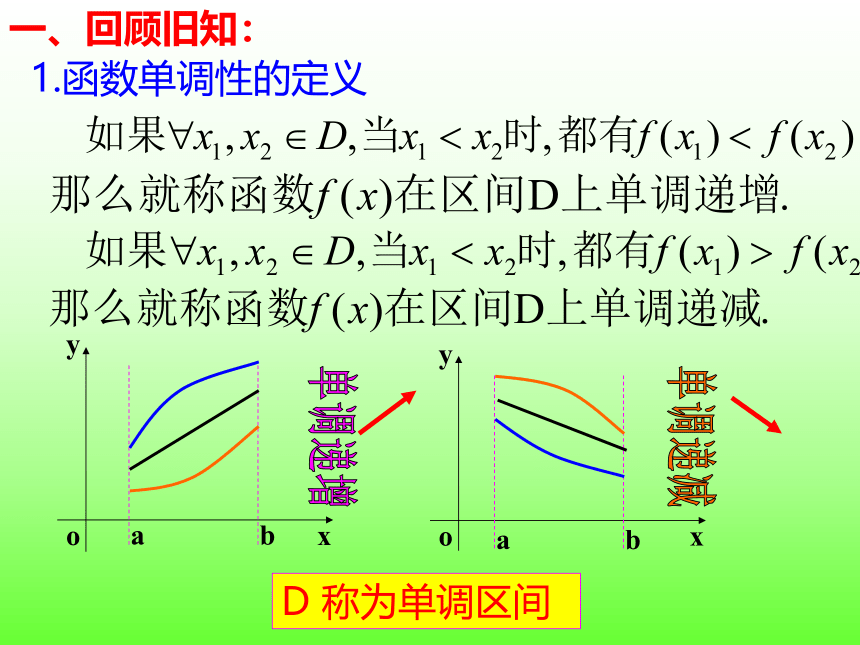
单调递增
单调递减
D 称为单调区间
1.函数单调性的定义
一、回顾旧知:
3).变 形:通常是因式分解和配方;
5).下结论:指出函数f(x)在给定的区间D上的单调性.
4). 定 号:判断差f(x1)-f(x2)的正负;
2). 作 差:f(x1)-f(x2);
2.判断函数单调性的一般步骤 :
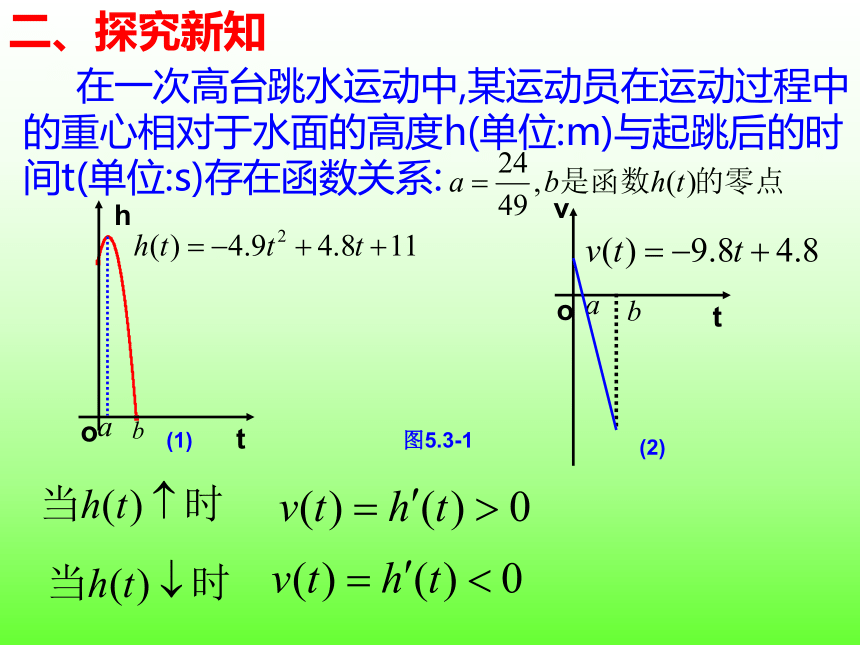
1). 任 值: x1,x2∈D,且x1二、探究新知
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系:
h
t
o
v
t
o
图5.3-1
(1)
(2)
x
y
O
x
y
O
x
y
O
x
y
O
y = x
y = x2
y = x3
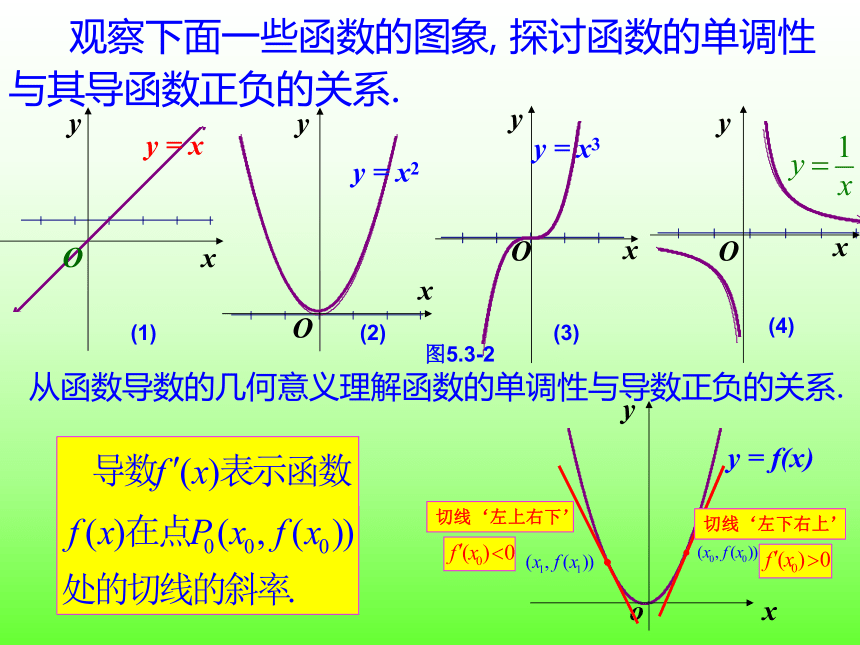
观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系.
图5.3-2
(1)
(2)
(3)
(4)
从函数导数的几何意义理解函数的单调性与导数正负的关系.
x
y
o
y = f(x)
切线‘左下右上’
切线‘左上右下’
注意:应正确理解 “ 某个区间 ” 的含义,它必是定义域内的某个区间.
如果恒有 ,则 是常数.
函数f(x)的单调性与导函数 正负的关系如下:
1.例1.利用导数判断下列函数的单调性:
解:
(1) 因为 , 所以
(2) 因为 , 所以
因此, 函数 在 上单调递增.
当 , 即 时,
函数 单调递增;
当 , 即 时,
函数 单调递减.
三、巩固新知
解:
(3) 因为 , 所以
因此, 函数 在 上单调递减.
1.例1.判断下列函数的单调性, 并求出单调区间:
①求定义域
②求
③令
④作出结论
2.试总结用“导数法”求单调区间的步骤?
注:单调区间不以“并集”出现.
3.例2.已知导函数 的下列信息:
试画出函数 的图象的大致形状.
x
y
O
1
4
图5.3-5
解:
如右图5.3-5
函数 的图象如图所示, 试画出导函数 图象的大致形状
O
a
b
x
4.变式训练1
y
y=f(x)
x
y
O
a
b
c
c
判断下列函数的单调性, 并求出单调区间:
5.变式训练2
6.例3.
解:
步骤?
判断下列函数的单调性, 并求出单调区间:
7.变式训练3
8.探究:
8.探究:
y = x3
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时, 函数的图象就比较“陡峭”(向上或向下),反之, 函数的图象就“平缓”一些.
9.例4.
解:
1.函数单调性与导数的关系
四、课堂小结
2.作业: 课本P97 习题5.3 2②④
5.3.1
函数的单调性
选择性必修 第二册 第五章 一元函数的导数及其应用
学习目标
1.结合实例,直观探索并掌握函数的单调性与
导数的关系;
2.能利用导数研究函数的单调性,明确导数与函数单调性的关系;
3.会求次数不超过三次的函数的单调区间
4.核心素养:直观想象、数学抽象、数学运算。
y
x
o
a
b
y
x
o
a
b
单调递增
单调递减
D 称为单调区间
1.函数单调性的定义
一、回顾旧知:
3).变 形:通常是因式分解和配方;
5).下结论:指出函数f(x)在给定的区间D上的单调性.
4). 定 号:判断差f(x1)-f(x2)的正负;
2). 作 差:f(x1)-f(x2);
2.判断函数单调性的一般步骤 :
1). 任 值: x1,x2∈D,且x1
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系:
h
t
o
v
t
o
图5.3-1
(1)
(2)
x
y
O
x
y
O
x
y
O
x
y
O
y = x
y = x2
y = x3
观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系.
图5.3-2
(1)
(2)
(3)
(4)
从函数导数的几何意义理解函数的单调性与导数正负的关系.
x
y
o
y = f(x)
切线‘左下右上’
切线‘左上右下’
注意:应正确理解 “ 某个区间 ” 的含义,它必是定义域内的某个区间.
如果恒有 ,则 是常数.
函数f(x)的单调性与导函数 正负的关系如下:
1.例1.利用导数判断下列函数的单调性:
解:
(1) 因为 , 所以
(2) 因为 , 所以
因此, 函数 在 上单调递增.
当 , 即 时,
函数 单调递增;
当 , 即 时,
函数 单调递减.
三、巩固新知
解:
(3) 因为 , 所以
因此, 函数 在 上单调递减.
1.例1.判断下列函数的单调性, 并求出单调区间:
①求定义域
②求
③令
④作出结论
2.试总结用“导数法”求单调区间的步骤?
注:单调区间不以“并集”出现.
3.例2.已知导函数 的下列信息:
试画出函数 的图象的大致形状.
x
y
O
1
4
图5.3-5
解:
如右图5.3-5
函数 的图象如图所示, 试画出导函数 图象的大致形状
O
a
b
x
4.变式训练1
y
y=f(x)
x
y
O
a
b
c
c
判断下列函数的单调性, 并求出单调区间:
5.变式训练2
6.例3.
解:
步骤?
判断下列函数的单调性, 并求出单调区间:
7.变式训练3
8.探究:
8.探究:
y = x3
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时, 函数的图象就比较“陡峭”(向上或向下),反之, 函数的图象就“平缓”一些.
9.例4.
解:
1.函数单调性与导数的关系
四、课堂小结
2.作业: 课本P97 习题5.3 2②④
