沪科版数学八年级上册 12.4 综合与实践 一次函数模型的应用(1) 教案
文档属性
| 名称 | 沪科版数学八年级上册 12.4 综合与实践 一次函数模型的应用(1) 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 90.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 07:55:37 | ||
图片预览

文档简介
12.4 综合与实践 一次函数模型的应用
◇教学目标◇
【知识与技能】
能结合对函数的关系式的分析,尝试对变量的变化规律进行预测。
熟练运用一次函数知识建立实际问题的数学模型,提高解决实际问题的能力.
【过程与方法】
经历活动过程,让学生认识数学在现实生活中的用途,发展学生运用数学知识解决实际问题的能力.
【情感、态度与价值观】
1.体会数学与生活的联系,了解数学的价值,加深对数学的理解和认识;
2.认识数学是解决实际问题的重要工具,了解数与形的联系以及事物之间的关系.
◇教学重难点◇
【教学重点】
根据题意写出函数关系式,建立实际问题的数学模型.
【教学难点】
运用一次函数解决实际问题.
◇教学过程◇
展示学习目标:
1.巩固一次函数知识,灵活运用变量关系解决相关实际问题;
2.有机地把各种数学模型通过函数统一起来使用,提高解决实
际问题的能力;(重点)
3.认识数学在现实生活中的意义,提高运用数学知识解决实际
问题的能力.(难点)
引入:求一次函数解析式是我们本学期函数学习的主要内容,掌握建立一次
函数模型以及在实际问题中利用一次函数解决问题,才是我们学习的目的。现实生活或具体情境中的很多问题或现象都可以抽象成数学问题,并通过建立合适的数学模型来表示数量关系和变化规律,并求出结果和讨论结果的意义。下面,我们一起看看昨天大家写的学案。
二、学案初步学习讲解
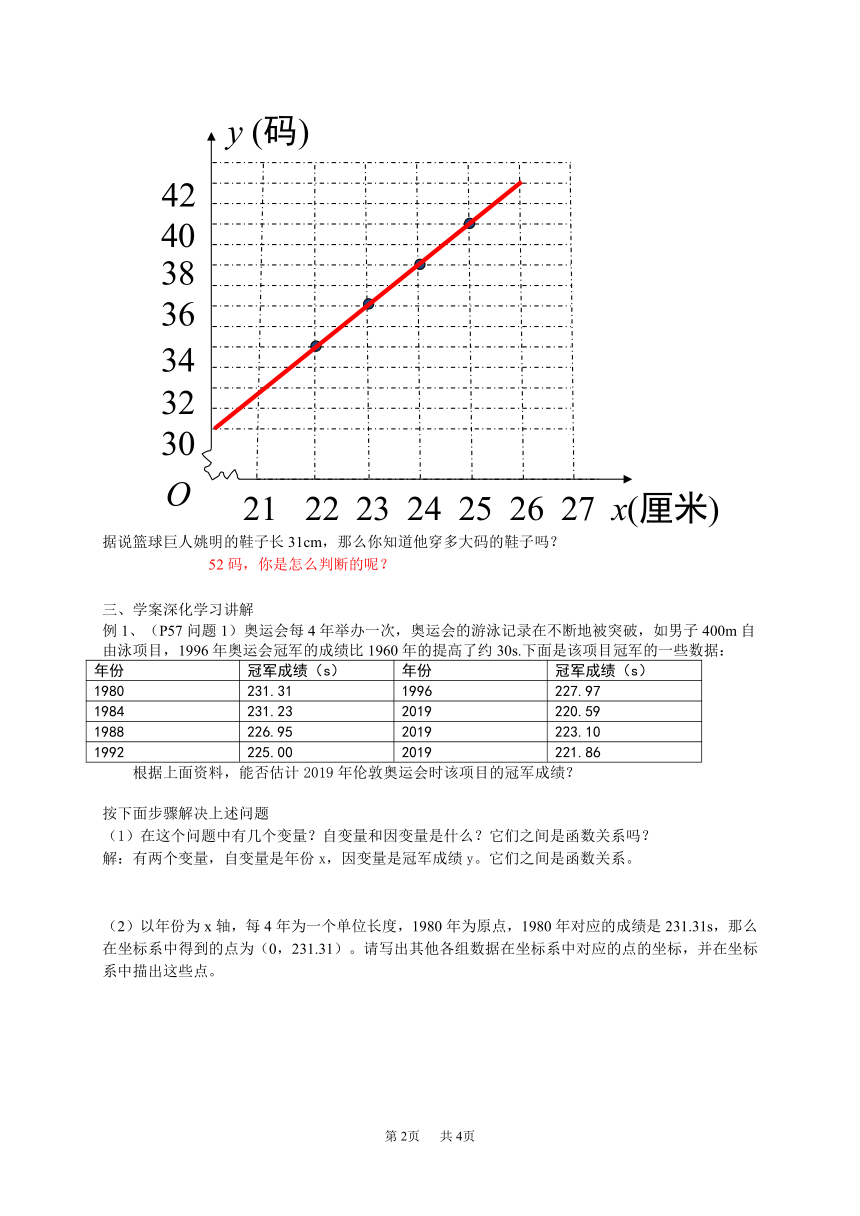
2、小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
x(厘米) … 22 25 23 26 24 …
y(码) … 34 40 36 42 38 …
(
根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
)
(
30
) (
32
) (
38
) (
36
) (
34
) (
42
) (
40
) (
23
) (
25
) (
24
) (
21
) (
22
) (
27
) (
26
) (
y
(
码
)
) (
x
(
厘米
)
) (
O
)
据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?
52码,你是怎么判断的呢?
三、学案深化学习讲解
例1、(P57问题1)奥运会每4年举办一次,奥运会的游泳记录在不断地被突破,如男子400m自由泳项目,1996年奥运会冠军的成绩比1960年的提高了约30s.下面是该项目冠军的一些数据:
年份 冠军成绩(s) 年份 冠军成绩(s)
1980 231.31 1996 227.97
1984 231.23 2019 220.59
1988 226.95 2019 223.10
1992 225.00 2019 221.86
根据上面资料,能否估计2019年伦敦奥运会时该项目的冠军成绩?
按下面步骤解决上述问题
(1)在这个问题中有几个变量?自变量和因变量是什么?它们之间是函数关系吗?
解:有两个变量,自变量是年份x,因变量是冠军成绩y。它们之间是函数关系。
(2)以年份为x轴,每4年为一个单位长度,1980年为原点,1980年对应的成绩是231.31s,那么在坐标系中得到的点为(0,231.31)。请写出其他各组数据在坐标系中对应的点的坐标,并在坐标系中描出这些点。
(
0
(
1980
)
230
1
(
1984
)
2
(
1988
)
3
(
1992
)
4
(
19
96
)
5
(
2000
)
6
(
2004
)
7
(
2008
)
8
(
2012
)
y/s
x/
年
210
220
200
240
) (
·
·
·
·
·
·
·
·
)
(3)观察描出的点的分布情况,猜测两个变量x、y之间是何种函数关系?
解:它们之间是一次函数关系。
(4)用待定系数法求出函数的解析式。
解:这里我们选取从原点向右的第三个点(1,231.23)及第7个点(7,221.86)的坐标代入y=kx+b中,得
解方程组可得:k=-1.63, b=232.86
所以,一次函数的解析式为:y=-1.63x+232.86
(5)根据所得的函数预测2019年和2019年两届奥运会的冠军成绩。
解:当把1980年的x值作为0,以后每增加4年得x的一个值,这样2019年时的x值为8,把x=8代入上式,得y=-1.63×8+232.86=219.82(s)
这样2019年时的x值为9,把x=9代入上式,得y=-1.63×9+232.86=218.19(s)
(
归纳总结
)
(
通过上面的学习,我们知道建立两个变量之间的函数模型,可以通过下列几个步骤完成:
)
(
(
1
)将实验得到的数据在直角坐标系中描出;(
2
)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;(
3
)进行检验;(
4
)应用这个函数模型解决问题
.
)
巩固提升
(
(1)
如果不采取任何措施,那么到第
5
年底,该地区沙漠面
积将增加多少万千米
2
?
)全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源已经成为一项十分紧迫的任务,某地区现有土地100万平方千米,沙漠200万平方千米,土地沙漠化的变化情况如下图所示.
(
第
50
年底后
) (
(2)
如果该地区沙漠的面积继续按此趋势扩大,那么从现在开始,第几年底后,该地区将丧失土地资源?
) (
10
万千米
2
)
(
(3)
如果从现在开始采取植树造林措施,每年改造
4
万千米
2
沙漠,那么到第几年底,该地区的沙漠面积能减少到
176
万千米
2
.
)
(
第
12
年底
)
四、本课小结
【小结】通过上面的探究,总结出建立函数模型来解决实际问题的步骤:
(1) 将实验得到的数据在直角坐标系中描出;
(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
(3)进行检验;
(4)应用函数模型解决问题。
作业布置
见《同步练习》本课时练习
第1页 共3页
◇教学目标◇
【知识与技能】
能结合对函数的关系式的分析,尝试对变量的变化规律进行预测。
熟练运用一次函数知识建立实际问题的数学模型,提高解决实际问题的能力.
【过程与方法】
经历活动过程,让学生认识数学在现实生活中的用途,发展学生运用数学知识解决实际问题的能力.
【情感、态度与价值观】
1.体会数学与生活的联系,了解数学的价值,加深对数学的理解和认识;
2.认识数学是解决实际问题的重要工具,了解数与形的联系以及事物之间的关系.
◇教学重难点◇
【教学重点】
根据题意写出函数关系式,建立实际问题的数学模型.
【教学难点】
运用一次函数解决实际问题.
◇教学过程◇
展示学习目标:
1.巩固一次函数知识,灵活运用变量关系解决相关实际问题;
2.有机地把各种数学模型通过函数统一起来使用,提高解决实
际问题的能力;(重点)
3.认识数学在现实生活中的意义,提高运用数学知识解决实际
问题的能力.(难点)
引入:求一次函数解析式是我们本学期函数学习的主要内容,掌握建立一次
函数模型以及在实际问题中利用一次函数解决问题,才是我们学习的目的。现实生活或具体情境中的很多问题或现象都可以抽象成数学问题,并通过建立合适的数学模型来表示数量关系和变化规律,并求出结果和讨论结果的意义。下面,我们一起看看昨天大家写的学案。
二、学案初步学习讲解
2、小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
x(厘米) … 22 25 23 26 24 …
y(码) … 34 40 36 42 38 …
(
根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
)
(
30
) (
32
) (
38
) (
36
) (
34
) (
42
) (
40
) (
23
) (
25
) (
24
) (
21
) (
22
) (
27
) (
26
) (
y
(
码
)
) (
x
(
厘米
)
) (
O
)
据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?
52码,你是怎么判断的呢?
三、学案深化学习讲解
例1、(P57问题1)奥运会每4年举办一次,奥运会的游泳记录在不断地被突破,如男子400m自由泳项目,1996年奥运会冠军的成绩比1960年的提高了约30s.下面是该项目冠军的一些数据:
年份 冠军成绩(s) 年份 冠军成绩(s)
1980 231.31 1996 227.97
1984 231.23 2019 220.59
1988 226.95 2019 223.10
1992 225.00 2019 221.86
根据上面资料,能否估计2019年伦敦奥运会时该项目的冠军成绩?
按下面步骤解决上述问题
(1)在这个问题中有几个变量?自变量和因变量是什么?它们之间是函数关系吗?
解:有两个变量,自变量是年份x,因变量是冠军成绩y。它们之间是函数关系。
(2)以年份为x轴,每4年为一个单位长度,1980年为原点,1980年对应的成绩是231.31s,那么在坐标系中得到的点为(0,231.31)。请写出其他各组数据在坐标系中对应的点的坐标,并在坐标系中描出这些点。
(
0
(
1980
)
230
1
(
1984
)
2
(
1988
)
3
(
1992
)
4
(
19
96
)
5
(
2000
)
6
(
2004
)
7
(
2008
)
8
(
2012
)
y/s
x/
年
210
220
200
240
) (
·
·
·
·
·
·
·
·
)
(3)观察描出的点的分布情况,猜测两个变量x、y之间是何种函数关系?
解:它们之间是一次函数关系。
(4)用待定系数法求出函数的解析式。
解:这里我们选取从原点向右的第三个点(1,231.23)及第7个点(7,221.86)的坐标代入y=kx+b中,得
解方程组可得:k=-1.63, b=232.86
所以,一次函数的解析式为:y=-1.63x+232.86
(5)根据所得的函数预测2019年和2019年两届奥运会的冠军成绩。
解:当把1980年的x值作为0,以后每增加4年得x的一个值,这样2019年时的x值为8,把x=8代入上式,得y=-1.63×8+232.86=219.82(s)
这样2019年时的x值为9,把x=9代入上式,得y=-1.63×9+232.86=218.19(s)
(
归纳总结
)
(
通过上面的学习,我们知道建立两个变量之间的函数模型,可以通过下列几个步骤完成:
)
(
(
1
)将实验得到的数据在直角坐标系中描出;(
2
)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;(
3
)进行检验;(
4
)应用这个函数模型解决问题
.
)
巩固提升
(
(1)
如果不采取任何措施,那么到第
5
年底,该地区沙漠面
积将增加多少万千米
2
?
)全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源已经成为一项十分紧迫的任务,某地区现有土地100万平方千米,沙漠200万平方千米,土地沙漠化的变化情况如下图所示.
(
第
50
年底后
) (
(2)
如果该地区沙漠的面积继续按此趋势扩大,那么从现在开始,第几年底后,该地区将丧失土地资源?
) (
10
万千米
2
)
(
(3)
如果从现在开始采取植树造林措施,每年改造
4
万千米
2
沙漠,那么到第几年底,该地区的沙漠面积能减少到
176
万千米
2
.
)
(
第
12
年底
)
四、本课小结
【小结】通过上面的探究,总结出建立函数模型来解决实际问题的步骤:
(1) 将实验得到的数据在直角坐标系中描出;
(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
(3)进行检验;
(4)应用函数模型解决问题。
作业布置
见《同步练习》本课时练习
第1页 共3页
