京改版八下数学第14章复习课《探究一次函数与三角形面积》课件(共35张ppt)
文档属性
| 名称 | 京改版八下数学第14章复习课《探究一次函数与三角形面积》课件(共35张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 793.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 07:58:14 | ||
图片预览





文档简介
(共35张PPT)
探究一次函数与三角形
的面积
A
B
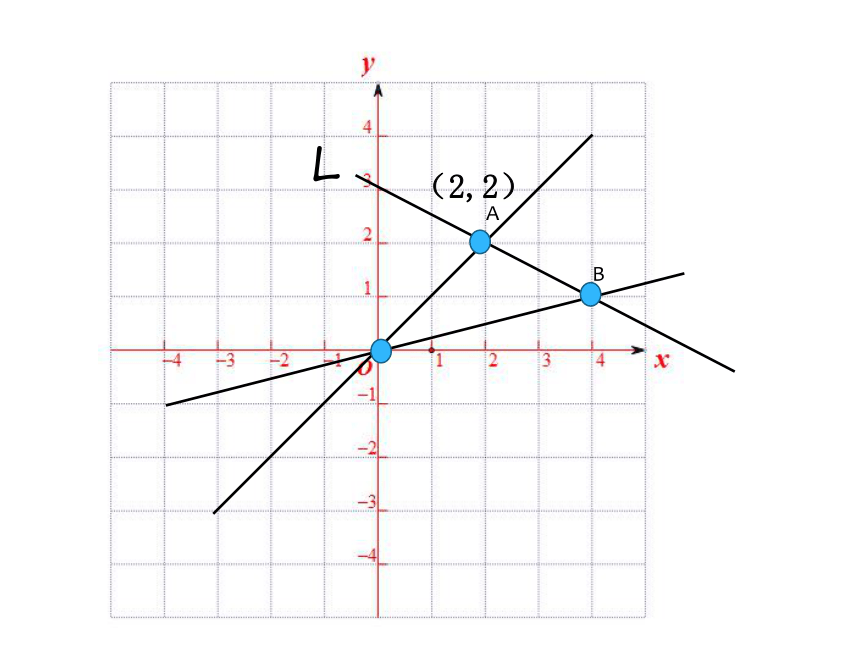
L
(2,2)
A
B
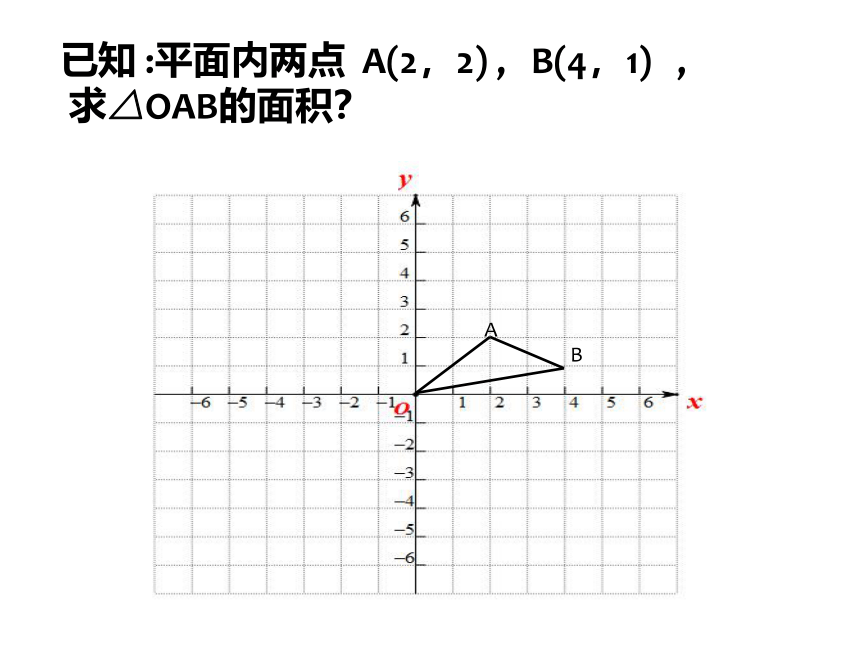
已知 :平面内两点 A(2,2) , B(4,1) ,
求△OAB的面积?
A
C
B
D
B
A
C
E
A
C
B
F
E
F
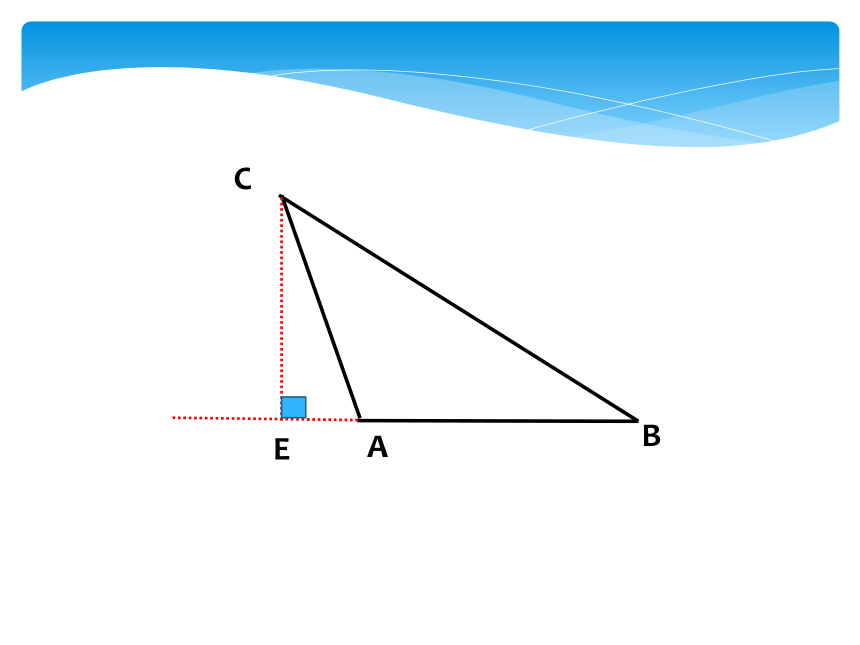
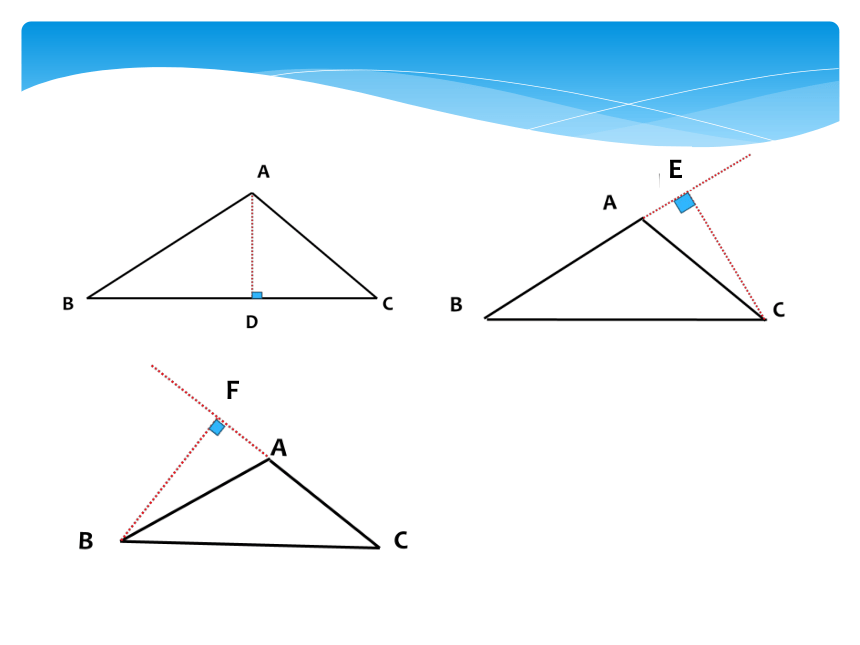
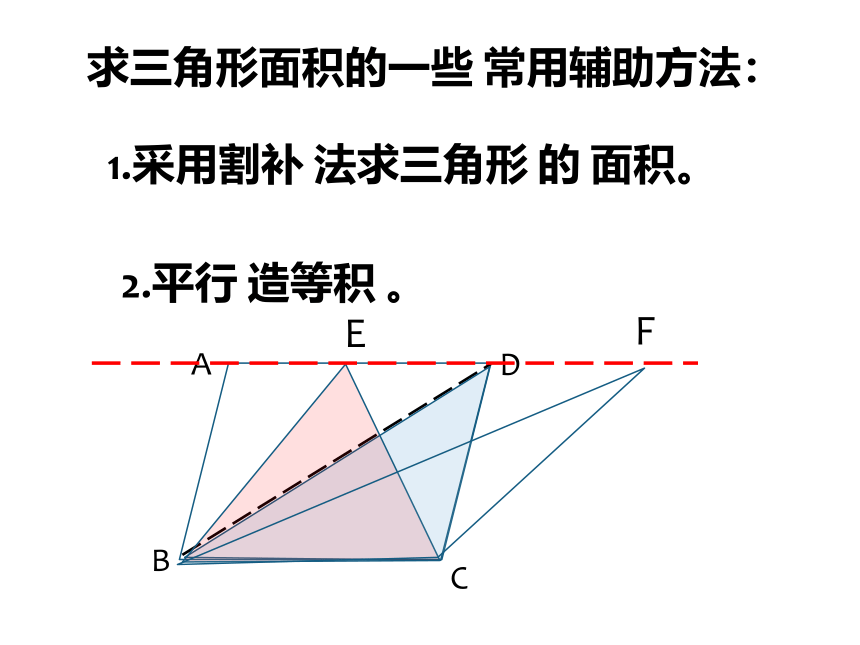
1.采用割补 法求三角形 的 面积。
2.平行 造等积 。
求三角形面积的一些 常用辅助方法:
A
D
C
B
E
F
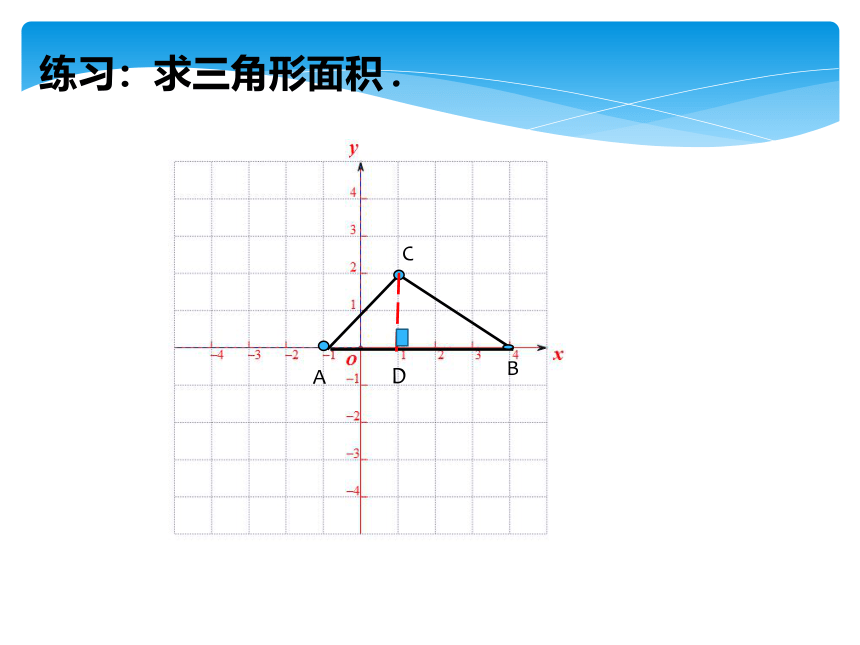
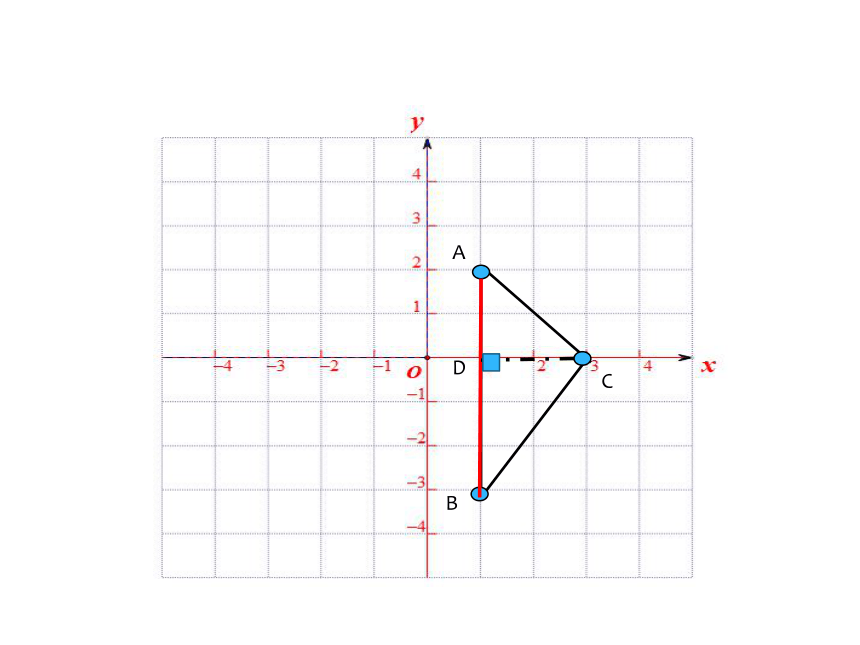
练习:求三角形面积 .
A
C
B
D
A
C
B
D
总结:平放或竖放的三角形求面积时:
底:
2.高:利用三角形顶点的坐标求。
│AB│=│x1-x2│
0
x1
x2
A
B
│AB│=│x1-x2│
A
B
斜放的△OAB如何求面积?
法一:采用割补法求三角形的面积。
法二:利用一次函数构造新三角形求面积。
D
D
D
法三:平行造等积。
M
a
M
b
M
c
如何求平面直角坐标系下任意△ABC的面积?
A
B
c
A
B
c
思考与提高:
如图,已知直线y=x+3的图象与x轴、y轴分别
交于A、 B两点,直线 l 经过原点,与线段AB交
于点C,把⊿AOB的面积分为2:1的两部分,求
直线l所对应的函数表达式?
B
A
C
分析题意,并完成下列填空:
1.S⊿AOC:S⊿AOB=_________
2.⊿AOC与⊿AOB共用的底
是_________.yc:OB=______.
3.点C的坐标为_______.
4.直线OC的解析式为____________.
C
2k
1k
3k
E
C
2k
1k
E
还有其他情况吗?
小结与提升:
1.割补法
2.平行造等积
3.直接或间接法
1.利用一次函数构造新的三角形求面积
数形结合的思想方法
数
形
2.利用间接法求三角形面积
转化的思想方法
探究一次函数与三角形
的面积
A
B
L
(2,2)
A
B
已知 :平面内两点 A(2,2) , B(4,1) ,
求△OAB的面积?
A
C
B
D
B
A
C
E
A
C
B
F
E
F
1.采用割补 法求三角形 的 面积。
2.平行 造等积 。
求三角形面积的一些 常用辅助方法:
A
D
C
B
E
F
练习:求三角形面积 .
A
C
B
D
A
C
B
D
总结:平放或竖放的三角形求面积时:
底:
2.高:利用三角形顶点的坐标求。
│AB│=│x1-x2│
0
x1
x2
A
B
│AB│=│x1-x2│
A
B
斜放的△OAB如何求面积?
法一:采用割补法求三角形的面积。
法二:利用一次函数构造新三角形求面积。
D
D
D
法三:平行造等积。
M
a
M
b
M
c
如何求平面直角坐标系下任意△ABC的面积?
A
B
c
A
B
c
思考与提高:
如图,已知直线y=x+3的图象与x轴、y轴分别
交于A、 B两点,直线 l 经过原点,与线段AB交
于点C,把⊿AOB的面积分为2:1的两部分,求
直线l所对应的函数表达式?
B
A
C
分析题意,并完成下列填空:
1.S⊿AOC:S⊿AOB=_________
2.⊿AOC与⊿AOB共用的底
是_________.yc:OB=______.
3.点C的坐标为_______.
4.直线OC的解析式为____________.
C
2k
1k
3k
E
C
2k
1k
E
还有其他情况吗?
小结与提升:
1.割补法
2.平行造等积
3.直接或间接法
1.利用一次函数构造新的三角形求面积
数形结合的思想方法
数
形
2.利用间接法求三角形面积
转化的思想方法
同课章节目录
