冀教版七下数学9.2.1三角形的内角和外角 课件(14张ppt)
文档属性
| 名称 | 冀教版七下数学9.2.1三角形的内角和外角 课件(14张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 08:00:30 | ||
图片预览



文档简介
(共14张PPT)
9.2 三角形的内角和外角
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷。
同学们,你们知道其中的道理吗?
内角三兄弟之争
情景引入
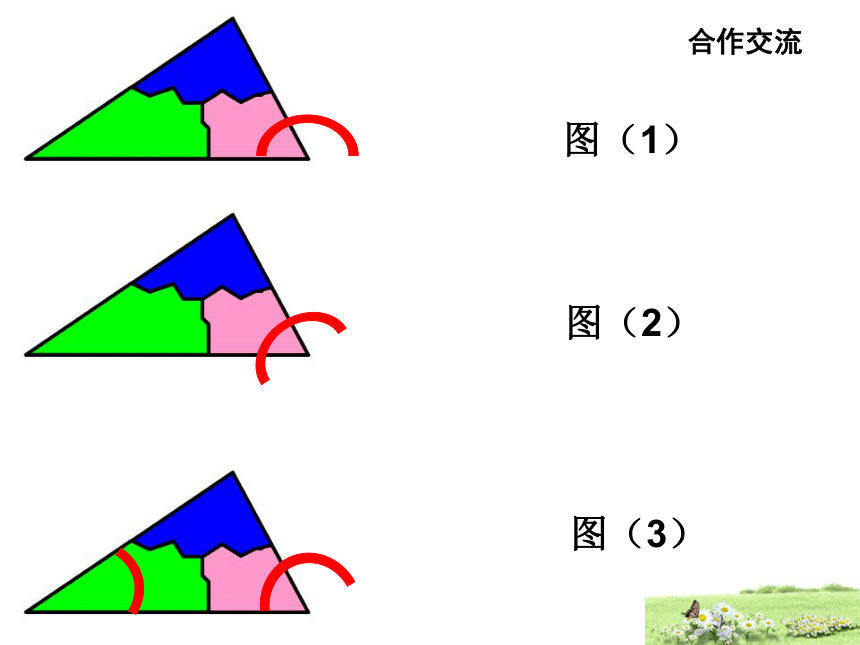
合作交流
图(1)
图(2)
图(3)
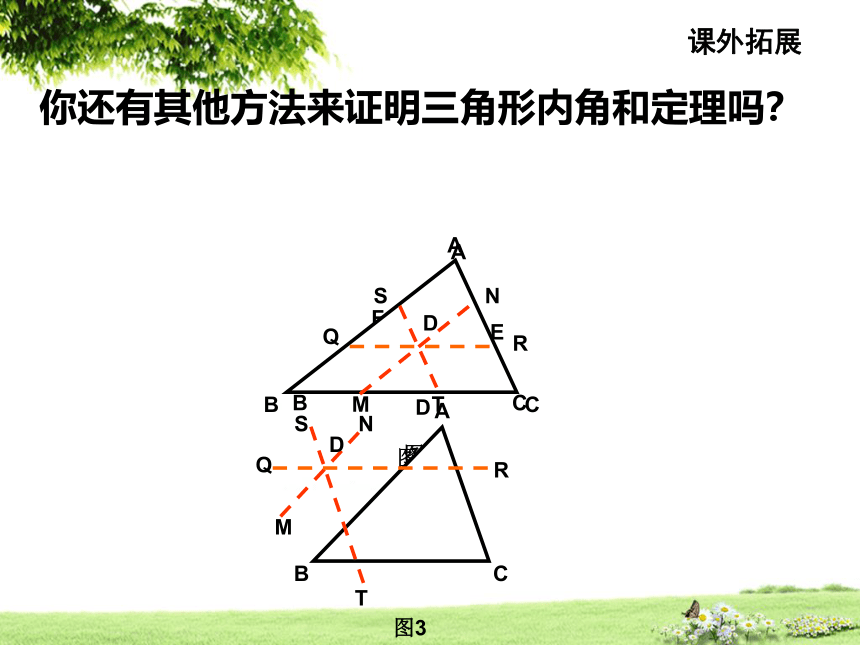
你还有其他方法来证明三角形内角和定理吗?
E
A
B
C
D
F
图1
A
N
B
C
T
S
图2
D
Q
R
M
A
N
B
C
T
S
图3
D
Q
R
M
课外拓展
三角形内角和定理
三角形内角和为180°.
数学语言:∵∠A+∠B+∠C=180°
(三角形内角和为180°)
∴∠A=180°-∠B-∠C
(等式的性质)
B
C
A
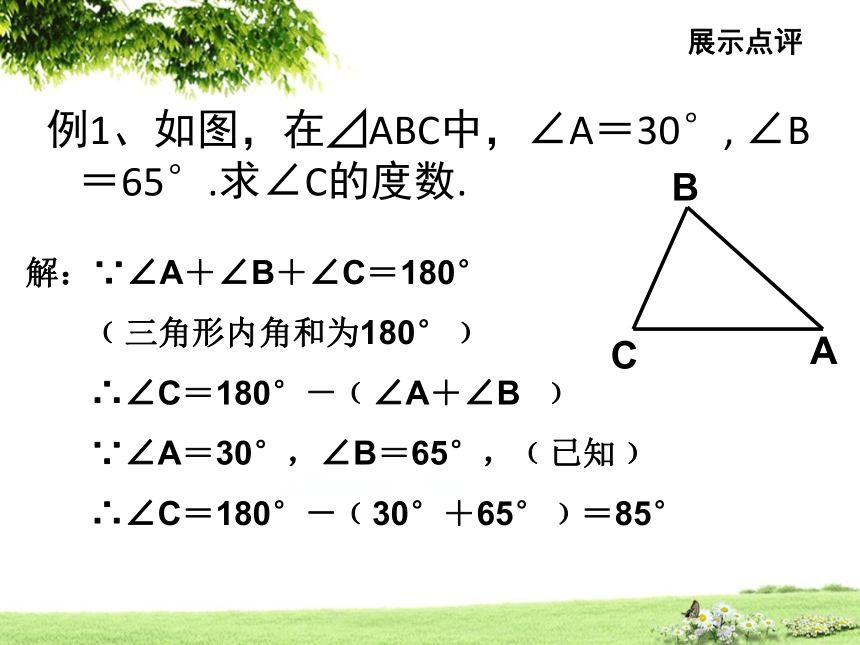
例1、如图,在⊿ABC中,∠A=30°, ∠B=65°.求∠C的度数.
B
C
A
解:∵∠A+∠B+∠C=180°
﹙三角形内角和为180°﹚
∴∠C=180°-﹙∠A+∠B ﹚
∵∠A=30°,∠B=65°,﹙已知﹚
∴∠C=180°-﹙30°+65°﹚=85°
展示点评
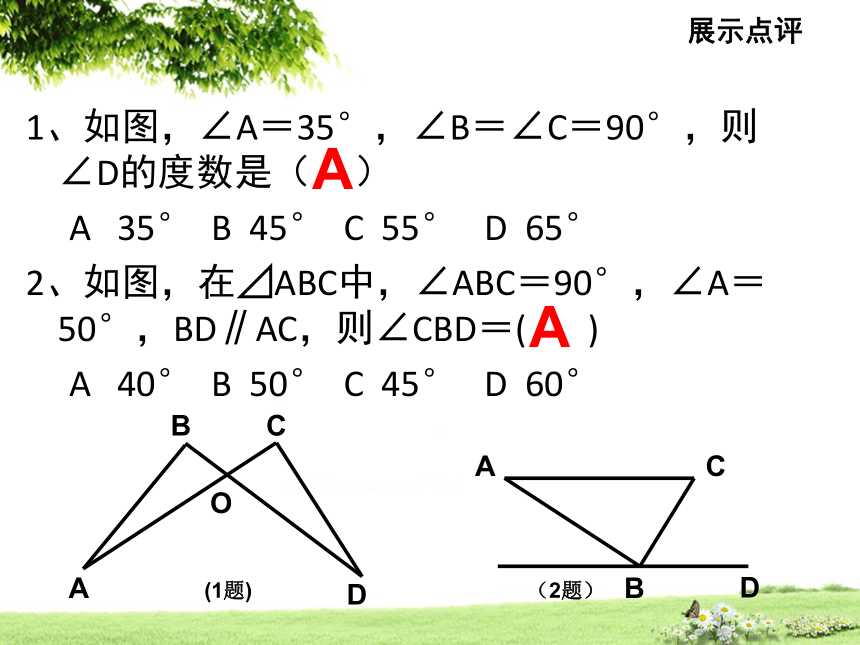
1、如图,∠A=35°,∠B=∠C=90°,则∠D的度数是( )
A 35° B 45° C 55° D 65°
2、如图,在⊿ABC中,∠ABC=90°,∠A=50°,BD∥AC,则∠CBD=( )
A 40° B 50° C 45° D 60°
展示点评
B
C
A
D
O
A
B
C
D
(1题)
(2题)
A
A
3、已知:如图,在△ABC中,DE∥BC,
∠A=60°∠C=70°,求:∠ADE的度数。
解:∵∠A=60°,∠C=70°,(已知)
∴ ∠B= 180°- ∠A- ∠C
= 180°- 60°- 70°
=50°(三角形内角和为180°)
∵ DE∥BC,(已知)
∴∠ADE=∠B =50°
(两直线平行,同位角相等)
B
C
D
E
A
展示点评
则∠A= x° ,∠B=2 x° , ∠C=6 x°.
∵∠A+∠B+∠C=180°(三角形内角和为180° )
∴ x + 2 x + 6 x =180
∴ x =20
∴ ∠A=20°
∠B=2×20°=40°
∠C=6×20°=120°
4、 在△ABC中,若∠A= ∠B= ∠C,求
∠A 、∠B和∠C的度数.
解:设∠A= ∠B = ∠C= x°
方程思想
展示点评
小结
1
三角形内角和定理:
2
3
三角形内角和为180°.
转化思想
方程思想
数学思想:
多种方法验证三角形内角和定理:
思路(1)转化为平角
(2)转化为同旁内角
(1-5号):B组1、2题
(6-9号):A组1、2题
作业:
作业
A
B
C
D
E
三角形内角和定理的验证
返回
已知:△ABC,
求证:∠A+∠B+∠C=180°
转化思想
A
B
C
A
B
C
D
E
三角形内角和定理的验证
已知:△ABC,
求证:
∠A+∠B+∠C=180°
返回
A
B
C
A
B
C
D
三角形内角和定理的验证
已知:△ABC,
求证:∠A+∠B+∠C=180°
返回
A
B
C
9.2 三角形的内角和外角
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷。
同学们,你们知道其中的道理吗?
内角三兄弟之争
情景引入
合作交流
图(1)
图(2)
图(3)
你还有其他方法来证明三角形内角和定理吗?
E
A
B
C
D
F
图1
A
N
B
C
T
S
图2
D
Q
R
M
A
N
B
C
T
S
图3
D
Q
R
M
课外拓展
三角形内角和定理
三角形内角和为180°.
数学语言:∵∠A+∠B+∠C=180°
(三角形内角和为180°)
∴∠A=180°-∠B-∠C
(等式的性质)
B
C
A
例1、如图,在⊿ABC中,∠A=30°, ∠B=65°.求∠C的度数.
B
C
A
解:∵∠A+∠B+∠C=180°
﹙三角形内角和为180°﹚
∴∠C=180°-﹙∠A+∠B ﹚
∵∠A=30°,∠B=65°,﹙已知﹚
∴∠C=180°-﹙30°+65°﹚=85°
展示点评
1、如图,∠A=35°,∠B=∠C=90°,则∠D的度数是( )
A 35° B 45° C 55° D 65°
2、如图,在⊿ABC中,∠ABC=90°,∠A=50°,BD∥AC,则∠CBD=( )
A 40° B 50° C 45° D 60°
展示点评
B
C
A
D
O
A
B
C
D
(1题)
(2题)
A
A
3、已知:如图,在△ABC中,DE∥BC,
∠A=60°∠C=70°,求:∠ADE的度数。
解:∵∠A=60°,∠C=70°,(已知)
∴ ∠B= 180°- ∠A- ∠C
= 180°- 60°- 70°
=50°(三角形内角和为180°)
∵ DE∥BC,(已知)
∴∠ADE=∠B =50°
(两直线平行,同位角相等)
B
C
D
E
A
展示点评
则∠A= x° ,∠B=2 x° , ∠C=6 x°.
∵∠A+∠B+∠C=180°(三角形内角和为180° )
∴ x + 2 x + 6 x =180
∴ x =20
∴ ∠A=20°
∠B=2×20°=40°
∠C=6×20°=120°
4、 在△ABC中,若∠A= ∠B= ∠C,求
∠A 、∠B和∠C的度数.
解:设∠A= ∠B = ∠C= x°
方程思想
展示点评
小结
1
三角形内角和定理:
2
3
三角形内角和为180°.
转化思想
方程思想
数学思想:
多种方法验证三角形内角和定理:
思路(1)转化为平角
(2)转化为同旁内角
(1-5号):B组1、2题
(6-9号):A组1、2题
作业:
作业
A
B
C
D
E
三角形内角和定理的验证
返回
已知:△ABC,
求证:∠A+∠B+∠C=180°
转化思想
A
B
C
A
B
C
D
E
三角形内角和定理的验证
已知:△ABC,
求证:
∠A+∠B+∠C=180°
返回
A
B
C
A
B
C
D
三角形内角和定理的验证
已知:△ABC,
求证:∠A+∠B+∠C=180°
返回
A
B
C
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
