高中数学人教新课标A版选修2-2 1.1 变化率与导数(word含答案解析)
文档属性
| 名称 | 高中数学人教新课标A版选修2-2 1.1 变化率与导数(word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 77.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 10:28:32 | ||
图片预览

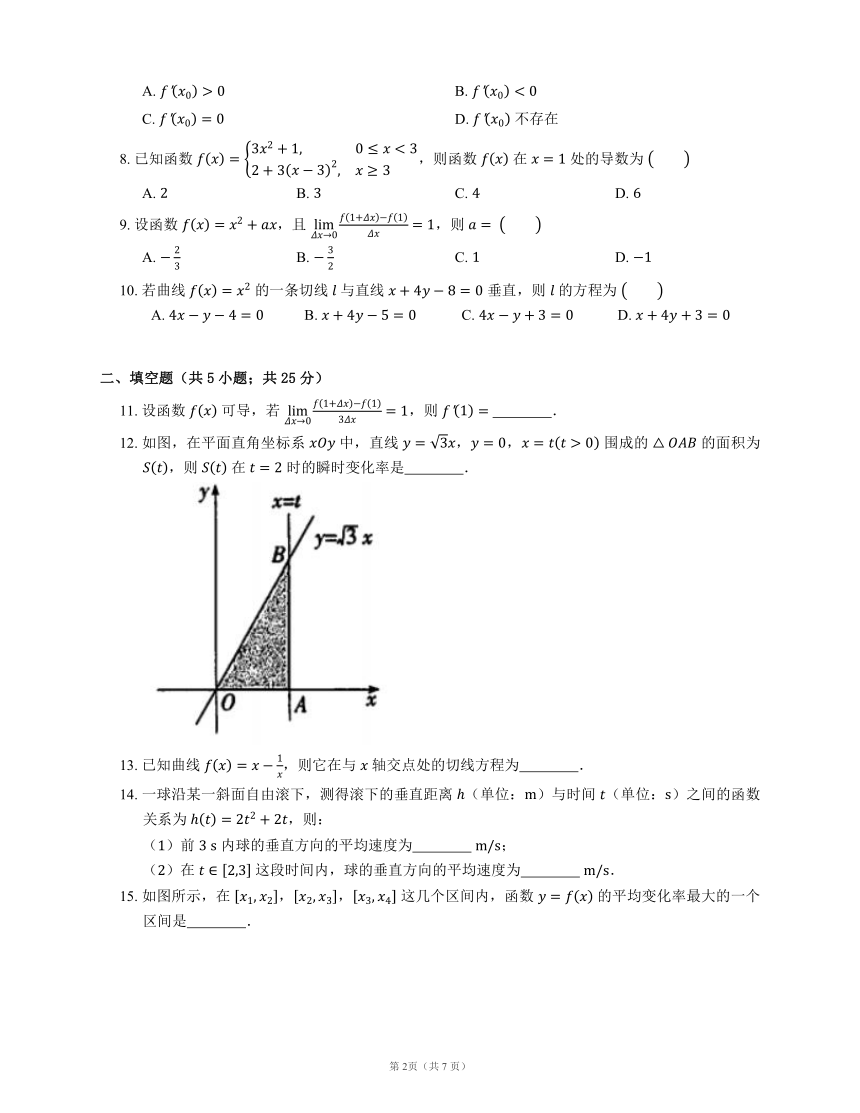

文档简介
1.1 变化率与导数
一、选择题(共10小题;共50分)
1. 已知函数 的图象如图所示,则 与 的大小关系是
A. B.
C. D. 不能确定
2. 设 为可导函数且满足 ,则曲线 在点 处的切线斜率为
A. B. C. D.
3. 下列各点中,在曲线 上,且曲线在该点处的切线的倾斜角为 的是
A. B. C. D.
4. 已知函数 在 处的导数为 ,则 等于
A. B. C. D.
5. 已知曲线 上一点 ,则曲线在点 处的切线的倾斜角为
A. B. C. D.
6. 已知函数 的图象如图所示,则下列不等关系中正确的是
A.
B.
C.
D.
7. 如果曲线 在点 处的切线方程为 ,那么
A. B.
C. D. 不存在
8. 已知函数 ,则函数 在 处的导数为
A. B. C. D.
9. 设函数 ,且 ,则
A. B. C. D.
10. 若曲线 的一条切线 与直线 垂直,则 的方程为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 设函数 可导,若 ,则 .
12. 如图,在平面直角坐标系 中,直线 ,, 围成的 的面积为 ,则 在 时的瞬时变化率是 .
13. 已知曲线 ,则它在与 轴交点处的切线方程为 .
14. 一球沿某一斜面自由滚下,测得滚下的垂直距离 (单位:)与时间 (单位:)之间的函数关系为 ,则:
()前 内球的垂直方向的平均速度为 ;
()在 这段时间内,球的垂直方向的平均速度为 .
15. 如图所示,在 ,, 这几个区间内,函数 的平均变化率最大的一个区间是 .
三、解答题(共3小题;共39分)
16. 设某质点的运动方程是 .求:
(1)该质点在 时的速度的大小;
(2)该质点运动的加速度方程.
17. 已知直线 为曲线 在点 处的切线, 为该曲线的另一条切线,且 ,求直线 的方程.
18. 已知曲线 在点 处的切线与 轴,直线 围成的三角形的面积为 ,求 的值.
答案
第一部分
1. B 【解析】由导数的几何意义,知 , 分别是函数 的图象在点 , 处切线的斜率,
由题中图象可知 .
2. B 【解析】易知
根据导数的定义可得 .
故曲线 在点 处的切线斜率为 .
3. D 【解析】设切点坐标为 ,
则 ,
所以 ,.
4. B 【解析】因为函数 在 处的导数为 ,
所以
5. B
【解析】曲线 在点 处的切线的斜率为
所以曲线在点 处的切线的倾斜角为 .
6. C 【解析】A,B两点连线的斜率 ,
为函数 的图象在点 处的切线的斜率,
为函数 的图象在点 处的切线的斜率,
根据题中图象可知 .
7. B 【解析】因为切线 的斜率为 ,
所以 .
8. D 【解析】易得 ,
9. D 【解析】因为 ,
所以
所以 ,解得 .
10. A
【解析】设切点为 ,
易得 .
由题意可知,切线 的斜率 ,即 ,所以 ,
所以切点坐标为 ,切线 的方程为 ,
即 .
第二部分
11.
【解析】因为 ,
所以 ,,
故 .
12.
【解析】 时,,则 ,则 ,
所以 ,
所以 .
13. 或
【解析】曲线 与 轴交点的坐标为 ,,
易知函数 在 处的导数
所以 ,,
所以所求切线方程为 或 ,即 或 .
14. ,
【解析】()由题意知,,,即前 内球的垂直方向的平均速度为 .
()由题意知,,,即这段时间内球的垂直方向的平均速度为 .
15.
【解析】根据平均变化率的定义,记函数 在区间 ,, 上的平均变化率分别为 ,,,则 ,,,结合题中图象可以发现 ,故函数 的平均变化率最大的一个区间是 .
第三部分
16. (1) 设质点运动的速度为 ,
则 ,
所以 ,
即质点在 时的速度的大小为 .
(2) 设质点运动的加速度为 .
因为 ,
所以 .
17. 因为
所以 ,
所以直线 的方程为 ,即 .
设直线 过曲线 上的 ,
则直线 的方程为 ,
因为 ,
所以 ,
解得 ,
所以直线 的方程为 .
18. 因为 ,
所以曲线 在点 处的切线斜率为 ,
所以切线方程为 ,即 .
令 ,得切线与 轴的交点为 ,
令 ,得 .
由题意知三角形面积为 ,
解得 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 已知函数 的图象如图所示,则 与 的大小关系是
A. B.
C. D. 不能确定
2. 设 为可导函数且满足 ,则曲线 在点 处的切线斜率为
A. B. C. D.
3. 下列各点中,在曲线 上,且曲线在该点处的切线的倾斜角为 的是
A. B. C. D.
4. 已知函数 在 处的导数为 ,则 等于
A. B. C. D.
5. 已知曲线 上一点 ,则曲线在点 处的切线的倾斜角为
A. B. C. D.
6. 已知函数 的图象如图所示,则下列不等关系中正确的是
A.
B.
C.
D.
7. 如果曲线 在点 处的切线方程为 ,那么
A. B.
C. D. 不存在
8. 已知函数 ,则函数 在 处的导数为
A. B. C. D.
9. 设函数 ,且 ,则
A. B. C. D.
10. 若曲线 的一条切线 与直线 垂直,则 的方程为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 设函数 可导,若 ,则 .
12. 如图,在平面直角坐标系 中,直线 ,, 围成的 的面积为 ,则 在 时的瞬时变化率是 .
13. 已知曲线 ,则它在与 轴交点处的切线方程为 .
14. 一球沿某一斜面自由滚下,测得滚下的垂直距离 (单位:)与时间 (单位:)之间的函数关系为 ,则:
()前 内球的垂直方向的平均速度为 ;
()在 这段时间内,球的垂直方向的平均速度为 .
15. 如图所示,在 ,, 这几个区间内,函数 的平均变化率最大的一个区间是 .
三、解答题(共3小题;共39分)
16. 设某质点的运动方程是 .求:
(1)该质点在 时的速度的大小;
(2)该质点运动的加速度方程.
17. 已知直线 为曲线 在点 处的切线, 为该曲线的另一条切线,且 ,求直线 的方程.
18. 已知曲线 在点 处的切线与 轴,直线 围成的三角形的面积为 ,求 的值.
答案
第一部分
1. B 【解析】由导数的几何意义,知 , 分别是函数 的图象在点 , 处切线的斜率,
由题中图象可知 .
2. B 【解析】易知
根据导数的定义可得 .
故曲线 在点 处的切线斜率为 .
3. D 【解析】设切点坐标为 ,
则 ,
所以 ,.
4. B 【解析】因为函数 在 处的导数为 ,
所以
5. B
【解析】曲线 在点 处的切线的斜率为
所以曲线在点 处的切线的倾斜角为 .
6. C 【解析】A,B两点连线的斜率 ,
为函数 的图象在点 处的切线的斜率,
为函数 的图象在点 处的切线的斜率,
根据题中图象可知 .
7. B 【解析】因为切线 的斜率为 ,
所以 .
8. D 【解析】易得 ,
9. D 【解析】因为 ,
所以
所以 ,解得 .
10. A
【解析】设切点为 ,
易得 .
由题意可知,切线 的斜率 ,即 ,所以 ,
所以切点坐标为 ,切线 的方程为 ,
即 .
第二部分
11.
【解析】因为 ,
所以 ,,
故 .
12.
【解析】 时,,则 ,则 ,
所以 ,
所以 .
13. 或
【解析】曲线 与 轴交点的坐标为 ,,
易知函数 在 处的导数
所以 ,,
所以所求切线方程为 或 ,即 或 .
14. ,
【解析】()由题意知,,,即前 内球的垂直方向的平均速度为 .
()由题意知,,,即这段时间内球的垂直方向的平均速度为 .
15.
【解析】根据平均变化率的定义,记函数 在区间 ,, 上的平均变化率分别为 ,,,则 ,,,结合题中图象可以发现 ,故函数 的平均变化率最大的一个区间是 .
第三部分
16. (1) 设质点运动的速度为 ,
则 ,
所以 ,
即质点在 时的速度的大小为 .
(2) 设质点运动的加速度为 .
因为 ,
所以 .
17. 因为
所以 ,
所以直线 的方程为 ,即 .
设直线 过曲线 上的 ,
则直线 的方程为 ,
因为 ,
所以 ,
解得 ,
所以直线 的方程为 .
18. 因为 ,
所以曲线 在点 处的切线斜率为 ,
所以切线方程为 ,即 .
令 ,得切线与 轴的交点为 ,
令 ,得 .
由题意知三角形面积为 ,
解得 .
第1页(共1 页)
