北师大版七年级下册数学第五章3简单的轴对称图形 同步检测卷(word版含解析)
文档属性
| 名称 | 北师大版七年级下册数学第五章3简单的轴对称图形 同步检测卷(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 252.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览


文档简介
北师大版同步检测卷:简单的轴对称图形
一、选择题(共10小题;共50分)
1. 三角形中,到三边距离相等的点是
A. 三条高线的交点 B. 三条中线的交点
C. 三条角平分线的交点 D. 三边垂直平分线的交点
2. 等腰三角形的一个角是 ,则它的底角是
A. B. 或 C. 或 D.
3. 甲、乙两位同学分别用尺规作图法作 的平分线 ,则他们两人的作图方法
A. 甲、乙两人均正确 B. 甲正确,乙错误
C. 甲错误,乙正确 D. 甲、乙两人均错误
4. 如图,要在一条河上架一座桥 (河的两岸互相平行,桥与河岸垂直),在如下四种方案中,使得 , 两地的路程最短的是
A. B.
C. D.
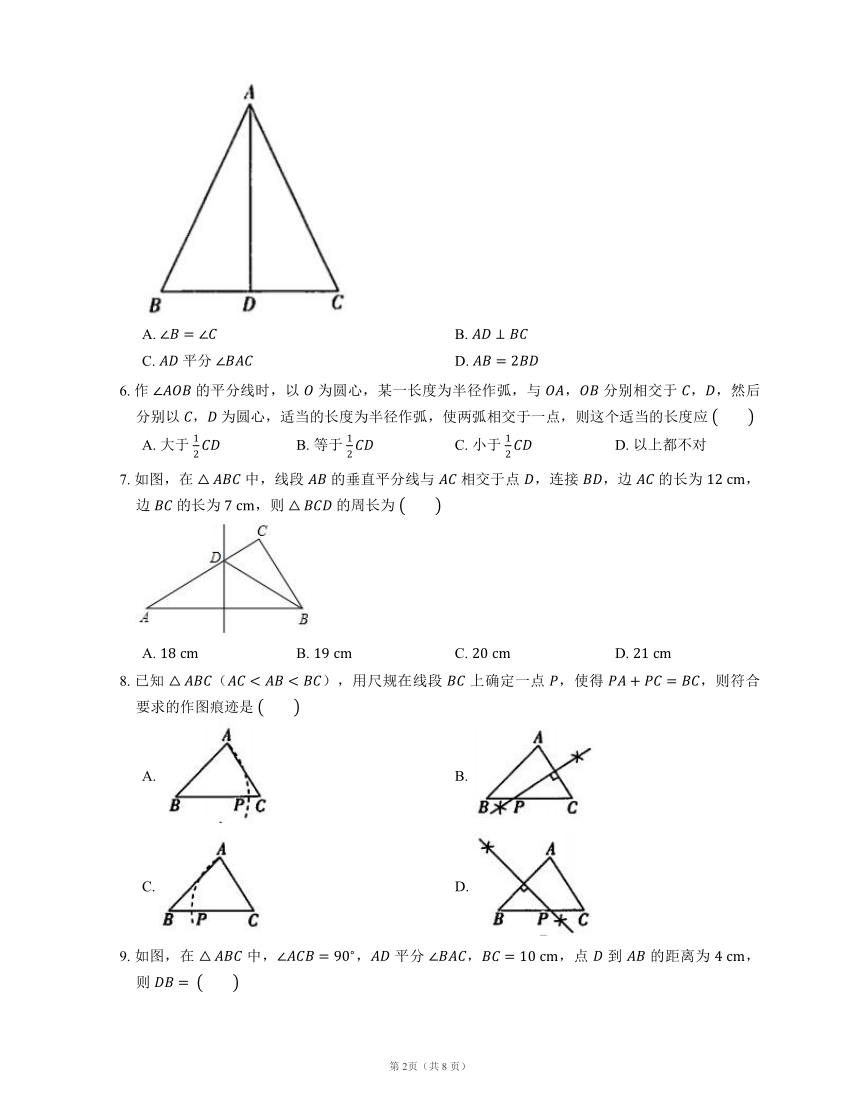
5. 如图,在 中,, 是 的中点,下列结论中不正确的是
A. B.
C. 平分 D.
6. 作 的平分线时,以 为圆心,某一长度为半径作弧,与 , 分别相交于 ,,然后分别以 , 为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度应
A. 大于 B. 等于 C. 小于 D. 以上都不对
7. 如图,在 中,线段 的垂直平分线与 相交于点 ,连接 ,边 的长为 ,边 的长为 ,则 的周长为
A. B. C. D.
8. 已知 (),用尺规在线段 上确定一点 ,使得 ,则符合要求的作图痕迹是
A. B.
C. D.
9. 如图,在 中,, 平分 ,,点 到 的距离为 ,则
A. B. C. D.
10. 小明不慎把家里的一块圆形玻璃打碎了,其中四块碎片如图所示,为配到一块与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是
A. 第①块 B. 第②块 C. 第③块 D. 第④块
二、填空题(共5小题;共25分)
11. 如图,一个旅游船从大桥 的 处前往山脚下的 处接游客,然后将游客送往河岸 上,再回到 处,请画出旅游船的最短路径(实际行走路径画实线,其它辅助线画虚线) .
12. 如图,已知 的周长为 ,根据图中尺规作图的痕迹,若 ,则 的周长为 .
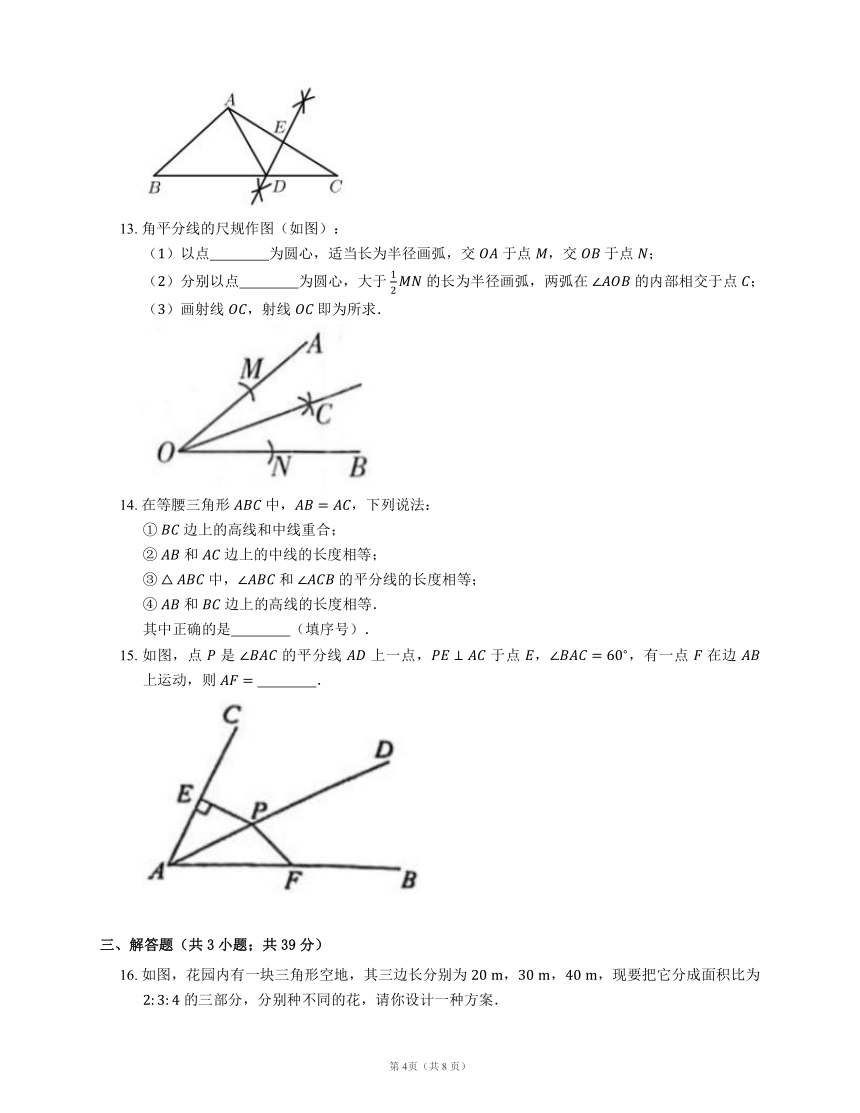
13. 角平分线的尺规作图(如图):
()以点 为圆心,适当长为半径画弧,交 于点 ,交 于点 ;
()分别以点 为圆心,大于 的长为半径画弧,两弧在 的内部相交于点 ;
()画射线 ,射线 即为所求.
14. 在等腰三角形 中,,下列说法:
① 边上的高线和中线重合;
② 和 边上的中线的长度相等;
③ 中, 和 的平分线的长度相等;
④ 和 边上的高线的长度相等.
其中正确的是 (填序号).
15. 如图,点 是 的平分线 上一点, 于点 ,,有一点 在边 上运动,则 .
三、解答题(共3小题;共39分)
16. 如图,花园内有一块三角形空地,其三边长分别为 ,,,现要把它分成面积比为 的三部分,分别种不同的花,请你设计一种方案.
17. 小芸在班级办黑板报时遇到了一个难题,在版面设计过程中需将一个半圆面三等分,请你帮助她设计一个合理的等分方案.要求用尺规作出图形,保留作图痕迹,并简要写出作法.
18. 如图所示,某小区广场有一块三角形绿地.为方便起见,将在绿地中建一凉亭,要使凉亭建在到三角形的三个顶点距离都相等的某处,假如你是工程师,你将如何确定凉亭的位置
答案
第一部分
1. C 【解析】三角形中,到三边距离相等的点是三条角平分线的交点.
2. B
3. C 【解析】由图知,甲、乙两位同学分别用尺规作图法作 的平分线 ,则他们两人的作图方法甲错误,乙正确.
4. B
5. D
【解析】 在 中,, 是 的中点,
,,,故A,B,C正确;
无法得到 ,故D不正确.
故选D.
6. A
7. B 【解析】 线段 的垂直平分线与 相交于点 ,
,
的周长 ,
,,
的周长 .
8. D 【解析】由 ,可得 ,则点 在线段 的垂直平分线上.
9. A 【解析】过点 作 于 ,
由题意得,,
平分 ,,,
,
,
故选:A.
10. A
【解析】要配到与原来大小一样的圆形玻璃,关键是确定圆的半径.小明带到商店去的一块玻璃碎片应该是第①块,可以在第①块碎片的圆弧上取两点,连接这两点得到一条弦,然后作这条弦的垂直平分线,同样,再作另一条弦的垂直平分线,两条垂直平分线的交点即为圆心,从而确定半径,该圆即可确定.
第二部分
11. 如图所示:
【解析】如图所示,作点 关于 的对称点 ,连接 交 于点 ,连接 .
最短路径为:.
12.
【解析】 的周长为 ,
,
为 的垂直平分线,,
,,
,
的周长为 .
13. ,,
14. ①②③
【解析】由 ,知 为底边,由等腰三角形的性质知①正确,由全等三角形的性质可判断②③正确.
15.
第三部分
16. 如图,方案为分别作 和 的平分线,设 和 的平分线的交点为 ,连接 ,则 ,, 的面积比为 .
17. ()作 的垂直平分线 交 于点 ;
()分别以 , 为圆心,以 (或 )的长为半径画弧,分别交半圆于点 ,;
()连接 , 即可.
18. ①分别以 , 为圆心,大于 的同样长为半径作弧,两弧相交于 , 两点,作直线 ;
②分别以 , 为圆心,大于 的同样长为半径作弧,两弧相交于 , 两点,作直线 ;
③ 与 的交点为 ,则 点即为所求.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 三角形中,到三边距离相等的点是
A. 三条高线的交点 B. 三条中线的交点
C. 三条角平分线的交点 D. 三边垂直平分线的交点
2. 等腰三角形的一个角是 ,则它的底角是
A. B. 或 C. 或 D.
3. 甲、乙两位同学分别用尺规作图法作 的平分线 ,则他们两人的作图方法
A. 甲、乙两人均正确 B. 甲正确,乙错误
C. 甲错误,乙正确 D. 甲、乙两人均错误
4. 如图,要在一条河上架一座桥 (河的两岸互相平行,桥与河岸垂直),在如下四种方案中,使得 , 两地的路程最短的是
A. B.
C. D.
5. 如图,在 中,, 是 的中点,下列结论中不正确的是
A. B.
C. 平分 D.
6. 作 的平分线时,以 为圆心,某一长度为半径作弧,与 , 分别相交于 ,,然后分别以 , 为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度应
A. 大于 B. 等于 C. 小于 D. 以上都不对
7. 如图,在 中,线段 的垂直平分线与 相交于点 ,连接 ,边 的长为 ,边 的长为 ,则 的周长为
A. B. C. D.
8. 已知 (),用尺规在线段 上确定一点 ,使得 ,则符合要求的作图痕迹是
A. B.
C. D.
9. 如图,在 中,, 平分 ,,点 到 的距离为 ,则
A. B. C. D.
10. 小明不慎把家里的一块圆形玻璃打碎了,其中四块碎片如图所示,为配到一块与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是
A. 第①块 B. 第②块 C. 第③块 D. 第④块
二、填空题(共5小题;共25分)
11. 如图,一个旅游船从大桥 的 处前往山脚下的 处接游客,然后将游客送往河岸 上,再回到 处,请画出旅游船的最短路径(实际行走路径画实线,其它辅助线画虚线) .
12. 如图,已知 的周长为 ,根据图中尺规作图的痕迹,若 ,则 的周长为 .
13. 角平分线的尺规作图(如图):
()以点 为圆心,适当长为半径画弧,交 于点 ,交 于点 ;
()分别以点 为圆心,大于 的长为半径画弧,两弧在 的内部相交于点 ;
()画射线 ,射线 即为所求.
14. 在等腰三角形 中,,下列说法:
① 边上的高线和中线重合;
② 和 边上的中线的长度相等;
③ 中, 和 的平分线的长度相等;
④ 和 边上的高线的长度相等.
其中正确的是 (填序号).
15. 如图,点 是 的平分线 上一点, 于点 ,,有一点 在边 上运动,则 .
三、解答题(共3小题;共39分)
16. 如图,花园内有一块三角形空地,其三边长分别为 ,,,现要把它分成面积比为 的三部分,分别种不同的花,请你设计一种方案.
17. 小芸在班级办黑板报时遇到了一个难题,在版面设计过程中需将一个半圆面三等分,请你帮助她设计一个合理的等分方案.要求用尺规作出图形,保留作图痕迹,并简要写出作法.
18. 如图所示,某小区广场有一块三角形绿地.为方便起见,将在绿地中建一凉亭,要使凉亭建在到三角形的三个顶点距离都相等的某处,假如你是工程师,你将如何确定凉亭的位置
答案
第一部分
1. C 【解析】三角形中,到三边距离相等的点是三条角平分线的交点.
2. B
3. C 【解析】由图知,甲、乙两位同学分别用尺规作图法作 的平分线 ,则他们两人的作图方法甲错误,乙正确.
4. B
5. D
【解析】 在 中,, 是 的中点,
,,,故A,B,C正确;
无法得到 ,故D不正确.
故选D.
6. A
7. B 【解析】 线段 的垂直平分线与 相交于点 ,
,
的周长 ,
,,
的周长 .
8. D 【解析】由 ,可得 ,则点 在线段 的垂直平分线上.
9. A 【解析】过点 作 于 ,
由题意得,,
平分 ,,,
,
,
故选:A.
10. A
【解析】要配到与原来大小一样的圆形玻璃,关键是确定圆的半径.小明带到商店去的一块玻璃碎片应该是第①块,可以在第①块碎片的圆弧上取两点,连接这两点得到一条弦,然后作这条弦的垂直平分线,同样,再作另一条弦的垂直平分线,两条垂直平分线的交点即为圆心,从而确定半径,该圆即可确定.
第二部分
11. 如图所示:
【解析】如图所示,作点 关于 的对称点 ,连接 交 于点 ,连接 .
最短路径为:.
12.
【解析】 的周长为 ,
,
为 的垂直平分线,,
,,
,
的周长为 .
13. ,,
14. ①②③
【解析】由 ,知 为底边,由等腰三角形的性质知①正确,由全等三角形的性质可判断②③正确.
15.
第三部分
16. 如图,方案为分别作 和 的平分线,设 和 的平分线的交点为 ,连接 ,则 ,, 的面积比为 .
17. ()作 的垂直平分线 交 于点 ;
()分别以 , 为圆心,以 (或 )的长为半径画弧,分别交半圆于点 ,;
()连接 , 即可.
18. ①分别以 , 为圆心,大于 的同样长为半径作弧,两弧相交于 , 两点,作直线 ;
②分别以 , 为圆心,大于 的同样长为半径作弧,两弧相交于 , 两点,作直线 ;
③ 与 的交点为 ,则 点即为所求.
第1页(共1 页)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
