北师大版七年级下册1.5 平方差公式同步练习(word版含答案)
文档属性
| 名称 | 北师大版七年级下册1.5 平方差公式同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 90.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 09:06:22 | ||
图片预览

文档简介
北师大版同步检测卷:平方差公式
一、选择题(共10小题;共50分)
1.
A. B. C. D.
2. 从边长为 的大正方形纸板中挖去一个边长为 的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为
A. B.
C. D.
3. 下列算式中,计算结果为 的是
A. B.
C. D.
4. 计算 的结果是
A. B. C. D.
5. 计算:
A. B.
C. D.
6. 计算 的结果是
A. B. C. D.
7. 计算 的结果为
A. B. C. D.
8. 从前,古希腊一位庄园主把一块边长为 米()的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加 米,相邻的另一边减少 米,变成矩形土地继续租给你,租金不变,你也没有吃亏,你看如何 ”如果这样,你觉得张老汉的租地面积会
A. 没有变化 B. 变大了 C. 变小了 D. 无法确定
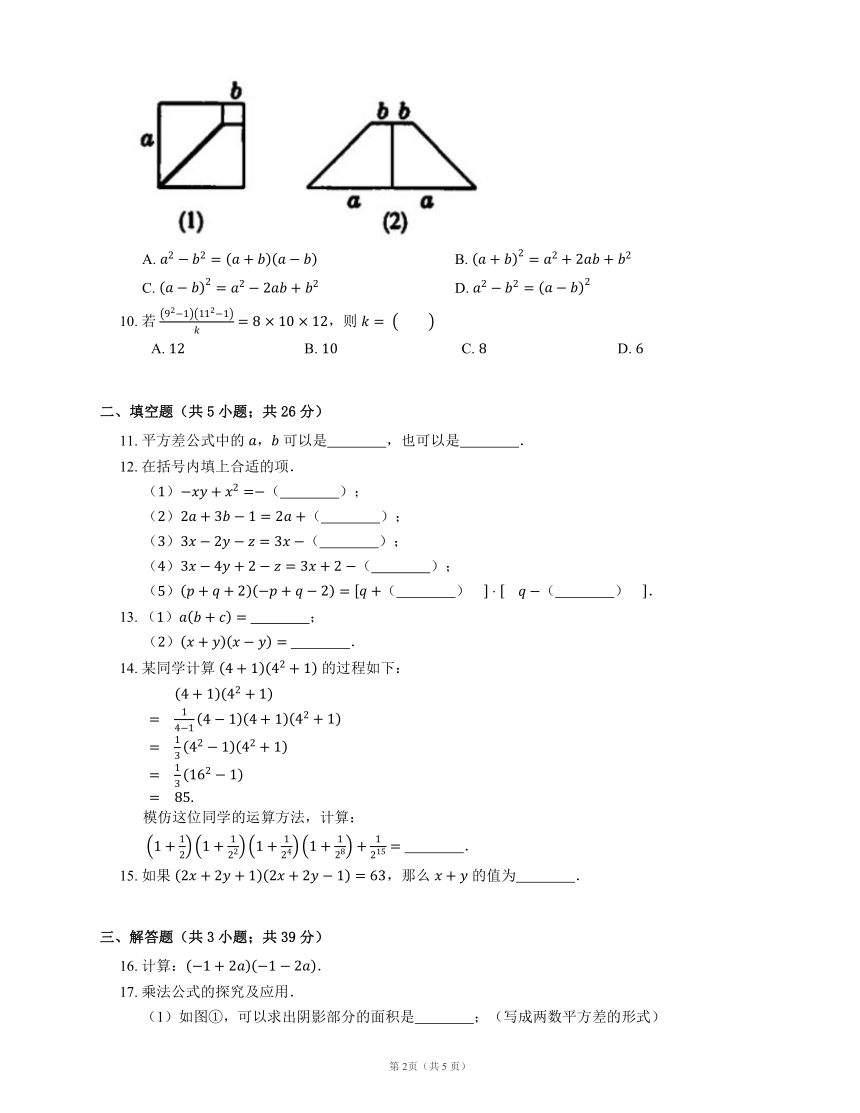
9. 在边长为 的正方形中挖去一个边长为 的小正方形(),再沿黑线剪开,如图()所示,然后拼成一个梯形,如图()所示.根据这两个图形的面积关系,表明下列式子成立的是
A. B.
C. D.
10. 若 ,则
A. B. C. D.
二、填空题(共5小题;共26分)
11. 平方差公式中的 , 可以是 ,也可以是 .
12. 在括号内填上合适的项.
()( );
()( );
()( );
()( );
()( )( ).
13. () ;
() .
14. 某同学计算 的过程如下:
模仿这位同学的运算方法,计算:
.
15. 如果 ,那么 的值为 .
三、解答题(共3小题;共39分)
16. 计算:.
17. 乘法公式的探究及应用.
(1)如图①,可以求出阴影部分的面积是 ;(写成两数平方差的形式)
(2)如图②,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 ,长是 ,面积是 ;(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式: (用式子表达);
(4)运用你所得到的公式,计算:.
18. 化简:.
答案
第一部分
1. C
2. D 【解析】由图 将小正方形一边向两方延长,得到两个梯形的高,两条高的和为 ,即平行四边形的高为 ,
两个图中的阴影部分的面积相等,
即甲的面积 ,乙的面积 .
即:.
验证成立的公式为:.
3. A
4. A
5. C
6. B
7. A 【解析】
8. C 【解析】矩形的面积为 ,
矩形的面积比正方形的面积 小了 平方米,
故选:C.
9. A
10. B
第二部分
11. 单项式,多项式
12. ,,,,,
13. ,
14.
15.
第三部分
16.
17. (1)
(2) ;;
(3)
(4)
18.
第1页(共1 页)
一、选择题(共10小题;共50分)
1.
A. B. C. D.
2. 从边长为 的大正方形纸板中挖去一个边长为 的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为
A. B.
C. D.
3. 下列算式中,计算结果为 的是
A. B.
C. D.
4. 计算 的结果是
A. B. C. D.
5. 计算:
A. B.
C. D.
6. 计算 的结果是
A. B. C. D.
7. 计算 的结果为
A. B. C. D.
8. 从前,古希腊一位庄园主把一块边长为 米()的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加 米,相邻的另一边减少 米,变成矩形土地继续租给你,租金不变,你也没有吃亏,你看如何 ”如果这样,你觉得张老汉的租地面积会
A. 没有变化 B. 变大了 C. 变小了 D. 无法确定
9. 在边长为 的正方形中挖去一个边长为 的小正方形(),再沿黑线剪开,如图()所示,然后拼成一个梯形,如图()所示.根据这两个图形的面积关系,表明下列式子成立的是
A. B.
C. D.
10. 若 ,则
A. B. C. D.
二、填空题(共5小题;共26分)
11. 平方差公式中的 , 可以是 ,也可以是 .
12. 在括号内填上合适的项.
()( );
()( );
()( );
()( );
()( )( ).
13. () ;
() .
14. 某同学计算 的过程如下:
模仿这位同学的运算方法,计算:
.
15. 如果 ,那么 的值为 .
三、解答题(共3小题;共39分)
16. 计算:.
17. 乘法公式的探究及应用.
(1)如图①,可以求出阴影部分的面积是 ;(写成两数平方差的形式)
(2)如图②,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 ,长是 ,面积是 ;(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式: (用式子表达);
(4)运用你所得到的公式,计算:.
18. 化简:.
答案
第一部分
1. C
2. D 【解析】由图 将小正方形一边向两方延长,得到两个梯形的高,两条高的和为 ,即平行四边形的高为 ,
两个图中的阴影部分的面积相等,
即甲的面积 ,乙的面积 .
即:.
验证成立的公式为:.
3. A
4. A
5. C
6. B
7. A 【解析】
8. C 【解析】矩形的面积为 ,
矩形的面积比正方形的面积 小了 平方米,
故选:C.
9. A
10. B
第二部分
11. 单项式,多项式
12. ,,,,,
13. ,
14.
15.
第三部分
16.
17. (1)
(2) ;;
(3)
(4)
18.
第1页(共1 页)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
