冀教版数学五年级下册 核心突破5.长方体、正方体的认识及其表面积的计算(含答案)
文档属性
| 名称 | 冀教版数学五年级下册 核心突破5.长方体、正方体的认识及其表面积的计算(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 67.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 13:07:51 | ||
图片预览


文档简介
核心考点突破卷
5.长方体、正方体的认识及其表面积的计算
一、填空。(每空3分,共18分)
1.数学课上,红红用学具棒搭一个长方体框架,搭了其中三根就能决定这个长方体框架的大小的是( )。(填序号)
2.聪聪用铁丝制作一个棱长为6厘米的正方体框架,他至少要用( )厘米的铁丝。(接头处忽略不计)
3.把一个长12厘米、宽10厘米、高10厘米的长方体罐头盒的侧面一圈贴上广告纸,至少用( )平方厘米的广告纸。
4.一个无盖的长方体玻璃鱼缸,长12 dm、宽6 dm、高10 dm,制作这个鱼缸至少需要( )dm2的玻璃。
5.把两个棱长是10厘米的正方体拼成一个长方体,这个长方体的表面积是( )平方厘米。
6.把一个长16厘米、宽6厘米、高8厘米的大长方体切成两个小长方体,这两个小长方体的表面积的和最大是( )平方厘米。
二、选择。(每小题5分,共25分)
1.用如图所示的硬纸板折成的长方体盒子的表面积是( )cm2。
A.13 B.12
C.10 D.8
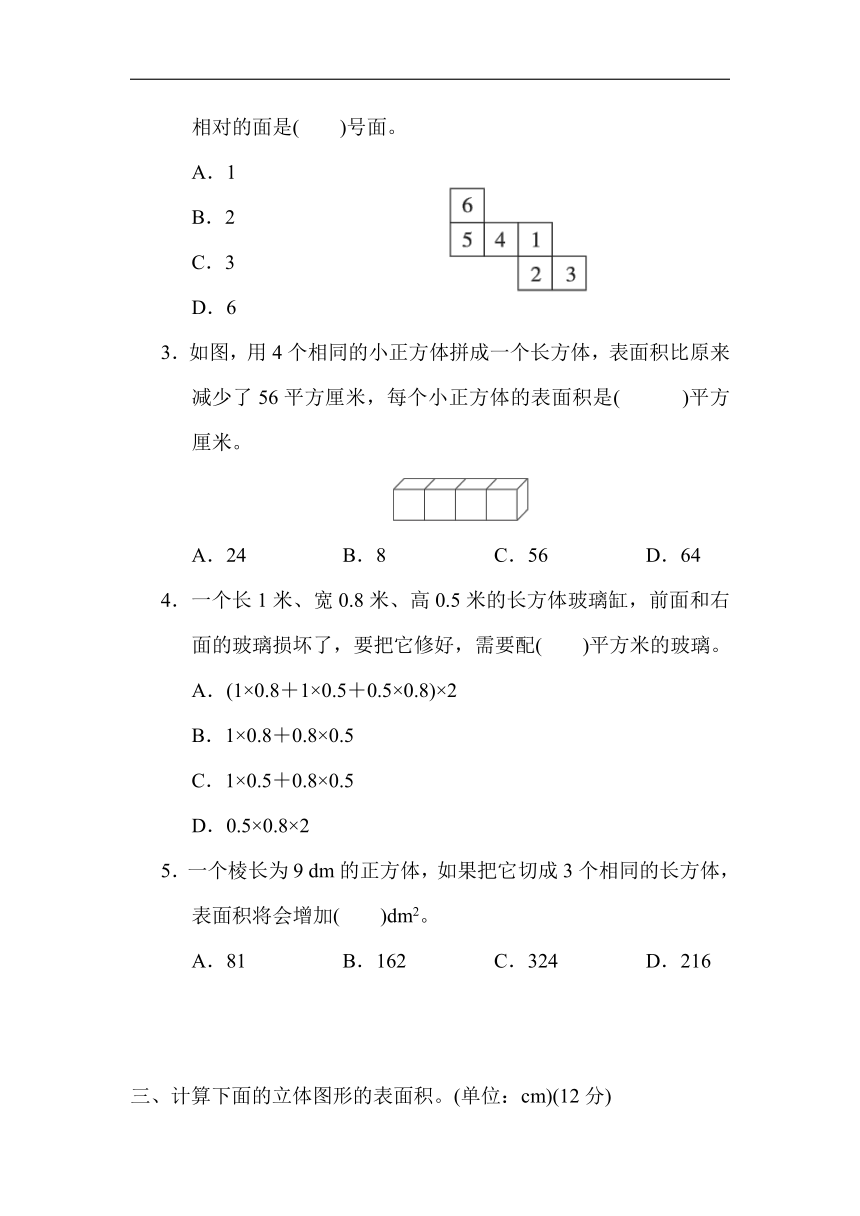
2.如图为一个正方体的展开图,与4号面相对的面是( )号面。
A.1
B.2
C.3
D.6
3.如图,用4个相同的小正方体拼成一个长方体,表面积比原来减少了56平方厘米,每个小正方体的表面积是( )平方厘米。
A.24 B.8 C.56 D.64
4.一个长1米、宽0.8米、高0.5米的长方体玻璃缸,前面和右面的玻璃损坏了,要把它修好,需要配( )平方米的玻璃。
A.(1×0.8+1×0.5+0.5×0.8)×2
B.1×0.8+0.8×0.5
C.1×0.5+0.8×0.5
D.0.5×0.8×2
5.一个棱长为9 dm的正方体,如果把它切成3个相同的长方体,表面积将会增加( )dm2。
A.81 B.162 C.324 D.216
三、计算下面的立体图形的表面积。(单位:cm)(12分)
四、解决问题。(共45分)
1.如图是一个用硬纸板制成的长方体影集封套,长31 cm、宽
27 cm、高2.5 cm,封套的右边不封口,做这个封套至少需要多少平方厘米的硬纸板?(9分)
2.教室里新建了一个长方体讲台,长3米、宽1.5米、高25厘米,现要在讲台外面抹上水泥,如果每平方米用水泥0.7千克,抹这个讲台需要准备多少千克水泥?(9分)
3.张老师家的客厅的长是6米,宽是4米,高是3米,门窗面积一共是8平方米。要粉刷客厅的四面墙壁和屋顶。
(1)需要粉刷的面积是多少平方米?(9分)
(2)如果每平方米用涂料1.5千克,那么一共要用涂料多少千克?(9分)
4.刘老师要用彩带捆扎一种礼盒(如图),如果打结部分的彩带长20 cm,刘老师捆扎一个这种礼盒需要彩带多少厘米?(9分)
答案
一、1.③ 2.72 3.440
4.432 【点拨】注意鱼缸是无盖的。
5.1000 【点拨】把两个正方体拼成一个长方体后,表面积比原来减少了正方体的2个面的面积,则这个长方体的表面积为10×10×(6×2-2)=1000(平方厘米)。
6.800 【点拨】要使两个小长方体的表面积的和最大,应增加大长方体两个最大面的面积。
二、1.A 2.C 3.C 4.C
5.C 【点拨】把正方体切成3个相同的长方体后,表面积增加了正方体的4个面的面积,即增加了9×9×4=324(dm2)。
三、10×10×6=600(cm2)
四、1. (27×31+27×2.5)×2+31×2.5
=(837+67.5)×2+77.5
=1809+77.5
=1886.5(cm2)
答:做这个封套至少需要1886.5 cm2的硬纸板。
2.25厘米=0.25米
3×1.5+3×0.25+1.5×0.25×2=6(平方米)
6×0.7=4.2(千克)
答:抹这个讲台需要准备4.2千克水泥。
【点拨】求抹水泥的面积时,只需计算讲台的四个面的面积和,不用加上讲台的底面和后面的面积。
3.(1) 6×4+(6×3+3×4)×2-8
=24+30×2-8
=84-8
=76(平方米)
答:需要粉刷的面积是76平方米。
(2)76×1.5=114(千克)
答:一共要用涂料114千克。
4.15×2+10×2+8×4+20=102(cm)
答:刘老师捆扎一个这种礼盒需要彩带102 cm。
【点拨】由题图可知,捆扎一个这种礼盒需要彩带的长度=
4条高+2条长+2条宽+打结部分彩带的长度。
5.长方体、正方体的认识及其表面积的计算
一、填空。(每空3分,共18分)
1.数学课上,红红用学具棒搭一个长方体框架,搭了其中三根就能决定这个长方体框架的大小的是( )。(填序号)
2.聪聪用铁丝制作一个棱长为6厘米的正方体框架,他至少要用( )厘米的铁丝。(接头处忽略不计)
3.把一个长12厘米、宽10厘米、高10厘米的长方体罐头盒的侧面一圈贴上广告纸,至少用( )平方厘米的广告纸。
4.一个无盖的长方体玻璃鱼缸,长12 dm、宽6 dm、高10 dm,制作这个鱼缸至少需要( )dm2的玻璃。
5.把两个棱长是10厘米的正方体拼成一个长方体,这个长方体的表面积是( )平方厘米。
6.把一个长16厘米、宽6厘米、高8厘米的大长方体切成两个小长方体,这两个小长方体的表面积的和最大是( )平方厘米。
二、选择。(每小题5分,共25分)
1.用如图所示的硬纸板折成的长方体盒子的表面积是( )cm2。
A.13 B.12
C.10 D.8
2.如图为一个正方体的展开图,与4号面相对的面是( )号面。
A.1
B.2
C.3
D.6
3.如图,用4个相同的小正方体拼成一个长方体,表面积比原来减少了56平方厘米,每个小正方体的表面积是( )平方厘米。
A.24 B.8 C.56 D.64
4.一个长1米、宽0.8米、高0.5米的长方体玻璃缸,前面和右面的玻璃损坏了,要把它修好,需要配( )平方米的玻璃。
A.(1×0.8+1×0.5+0.5×0.8)×2
B.1×0.8+0.8×0.5
C.1×0.5+0.8×0.5
D.0.5×0.8×2
5.一个棱长为9 dm的正方体,如果把它切成3个相同的长方体,表面积将会增加( )dm2。
A.81 B.162 C.324 D.216
三、计算下面的立体图形的表面积。(单位:cm)(12分)
四、解决问题。(共45分)
1.如图是一个用硬纸板制成的长方体影集封套,长31 cm、宽
27 cm、高2.5 cm,封套的右边不封口,做这个封套至少需要多少平方厘米的硬纸板?(9分)
2.教室里新建了一个长方体讲台,长3米、宽1.5米、高25厘米,现要在讲台外面抹上水泥,如果每平方米用水泥0.7千克,抹这个讲台需要准备多少千克水泥?(9分)
3.张老师家的客厅的长是6米,宽是4米,高是3米,门窗面积一共是8平方米。要粉刷客厅的四面墙壁和屋顶。
(1)需要粉刷的面积是多少平方米?(9分)
(2)如果每平方米用涂料1.5千克,那么一共要用涂料多少千克?(9分)
4.刘老师要用彩带捆扎一种礼盒(如图),如果打结部分的彩带长20 cm,刘老师捆扎一个这种礼盒需要彩带多少厘米?(9分)
答案
一、1.③ 2.72 3.440
4.432 【点拨】注意鱼缸是无盖的。
5.1000 【点拨】把两个正方体拼成一个长方体后,表面积比原来减少了正方体的2个面的面积,则这个长方体的表面积为10×10×(6×2-2)=1000(平方厘米)。
6.800 【点拨】要使两个小长方体的表面积的和最大,应增加大长方体两个最大面的面积。
二、1.A 2.C 3.C 4.C
5.C 【点拨】把正方体切成3个相同的长方体后,表面积增加了正方体的4个面的面积,即增加了9×9×4=324(dm2)。
三、10×10×6=600(cm2)
四、1. (27×31+27×2.5)×2+31×2.5
=(837+67.5)×2+77.5
=1809+77.5
=1886.5(cm2)
答:做这个封套至少需要1886.5 cm2的硬纸板。
2.25厘米=0.25米
3×1.5+3×0.25+1.5×0.25×2=6(平方米)
6×0.7=4.2(千克)
答:抹这个讲台需要准备4.2千克水泥。
【点拨】求抹水泥的面积时,只需计算讲台的四个面的面积和,不用加上讲台的底面和后面的面积。
3.(1) 6×4+(6×3+3×4)×2-8
=24+30×2-8
=84-8
=76(平方米)
答:需要粉刷的面积是76平方米。
(2)76×1.5=114(千克)
答:一共要用涂料114千克。
4.15×2+10×2+8×4+20=102(cm)
答:刘老师捆扎一个这种礼盒需要彩带102 cm。
【点拨】由题图可知,捆扎一个这种礼盒需要彩带的长度=
4条高+2条长+2条宽+打结部分彩带的长度。
同课章节目录
