2021-2022学年九年级数学上册 苏科版2.8圆锥的侧面积同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年九年级数学上册 苏科版2.8圆锥的侧面积同步练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 203.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 09:49:09 | ||
图片预览



文档简介
2.8圆锥的侧面积
一、单选题
1.已知圆锥的高为4 cm,底面半径为3 cm,那么,这个圆锥的侧面展开图扇形的圆心角的度数为( );
A.180° B.200° C.216° D.225°
2.如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm2、100cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,求甲的容积为何( )
A.1280cm3 B.2560cm3 C.3200cm3 D.4000cm3
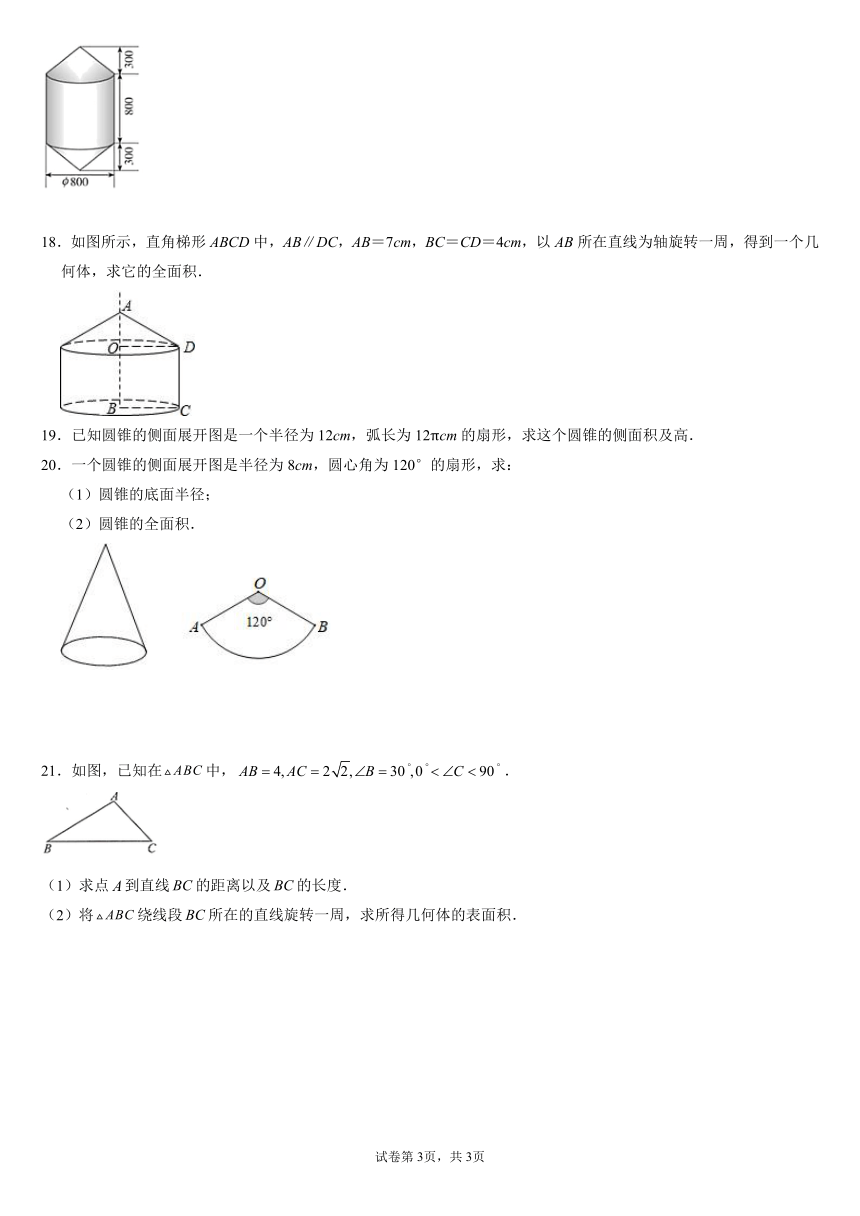
3.圆柱底面直径为2cm,高为4cm,则圆柱的侧面积为( )cm2
A.8π B.16π C.π D.2π
4.如图,圆锥体的高h=2cm,底面圆半径r=2cm,则圆锥体的全面积为( )cm2.
A.12π B.8π C.4π D.(4+4)π
5.如图,从一圆形纸片上剪出一个半径为R、圆心角为90°的扇形;和一半径为的圆,使之恰好围成如图所示的圆锥,则R与的关系为( )
A.R=2 B.R=4 C.R=2 D.R=6
6.一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的圆心角的度数是( )
A.120° B.180° C.240° D.300°
7.一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则做成这把遮阳伞需要布料的面积是( )平方米(接缝不计).
A.π B.5π C.4π D.3π
8.“赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8cm,圆柱体部分的高BC=6cm,圆锥体部分的高CD=3cm,则这个陀螺的表面积是( )
A.68πcm2 B.74πcm2 C.84πcm2 D.100πcm2
二、填空题
9.一个圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是______.
10.若一个圆锥的底面半径为1cm,它的侧面展开图的圆心角为90°,则这个圆锥的母线长为 cm.
11.设圆锥的底面半径为2,母线长为3,该圆锥的侧面积为 .
12.用一块弧长16πcm的扇形铁片,做一个高为6cm的圆锥形工件侧面(接缝忽略不计),那么这个扇形铁片的面积为 cm2.
13.如图,一把遮阳伞撑开时母线的长是3m,底面半径为2m,则做这把遮阳伞需用布料的面积是 m2.
14.如图,从直径为的圆形纸片上剪出一个圆心角为90°的扇形ABC.使点A、B、C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面半径是 .
15.圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是 .
16.如图将母线长为9的圆锥侧面展开后得到扇形的圆心角为120°,若将该扇形剪成两个同样的扇形再围成2个同样的圆锥,则新圆锥的底面半径是 .
三、解答题
17.如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:),电镀时,如果每平方米用锌,电镀100个这样的锚标浮筒,需要用多少锌?
18.如图所示,直角梯形ABCD中,AB∥DC,AB=7cm,BC=CD=4cm,以AB所在直线为轴旋转一周,得到一个几何体,求它的全面积.
19.已知圆锥的侧面展开图是一个半径为12cm,弧长为12πcm的扇形,求这个圆锥的侧面积及高.
20.一个圆锥的侧面展开图是半径为8cm,圆心角为120°的扇形,求:
(1)圆锥的底面半径;
(2)圆锥的全面积.
21.如图,已知在中,.
(1)求点到直线的距离以及的长度.
(2)将绕线段所在的直线旋转一周,求所得几何体的表面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【解析】圆锥的母线长为:
则:
解得
故选:C.
2.解:设高都为h,根据水的容积相等可列方程80×h=100×(h﹣8).解得h=40,所以甲的容积为40×80=3200,
故选:C.
3.解:π×2×4=8πcm2,故选A.
4.解:底面圆的半径为2,则底面周长=4π,
∵底面半径为2cm、高为2cm,
∴圆锥的母线长为4cm,
∴侧面面积=×4π×4=8π;
底面积为=4π,
全面积为:8π+4π=12πcm2.
故选:A.
5.B
【解析】扇形的弧长是:=,
圆的半径为r,则底面圆的周长是,
∵恰好围成如图所示的圆锥,
∴=,
∴R=4r,
故选:B.
6.解:设母线长为R,底面半径为r,
∴底面周长=2πr,底面面积=πr2,侧面面积=πrR,
∵侧面积是底面积的2倍,
∴2πr2=πrR,
∴R=2r,
设圆心角为n,
则=2πr=πR,
解得,n=180°,
故选:B.
7.解:圆锥的底面周长=2πr=2π×2=4π,
∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,
∴圆锥的侧面积=lr=×4π×2.5=5π,
故选:B.
8.解:∵底面圆的直径为8cm,高为3cm,
∴母线长为5cm,
∴其表面积=π×4×5+42π+8π×6=84πcm2,
故选:C.
9.3π
【解析】解:由题意可得,该圆锥的侧面积是×π×22=2π.该圆锥的底面的周长是2π,则底面圆半径是1,面积是π.所以该圆锥的全面积是:2π+π=3π.
故答案为:3π.
10.解:设母线长为lcm,
则=2π×1
解得:l=4.
故答案为:4.
11.解:该圆锥的侧面积=×2π×2×3=6π.
故答案为6π.
12.解:∵扇形铁片的弧长16πcm,
∴圆锥的底面周长为16πcm,
∴圆锥的底面半径==8(cm),
由勾股定理得:圆锥的母线长==10(cm),
∴扇形铁片的面积=×16π×10=80π(cm2)
故答案为:80π.
13.解:做这把遮阳伞需用布料的面积=×2π×2×3=6π(m2).
故答案为:6π.
14.解:连接BC,如图,
∵∠BAC=90°,
∴BC为⊙O的直径,即BC=8,
∴AB=BC=8,
设这个圆锥的底面半径为r,
根据题意得2πr=,
解得r=2,
即这个圆锥的底面半径为2.
故答案为2.
15.解:设圆锥的母线长为Rcm,
根据题意得2π 5=,
解得R=10.
即圆锥的母线长为10cm,
∴圆锥的高为:=5cm.
故答案为:5cm.
16.解:∵将该扇形剪成两个同样的扇形,大扇形的圆心角为120°,
∴新扇形的圆心角为60°,
∵扇形的母线长为9,
∴扇形的弧长是:=3π,
设底面半径是r,则2πr=3π,
解得:r=.
故答案为.
17.11.44πkg
【解析】解:由图形可知圆锥的底面圆的半径为400mm=0.4m,
圆锥的高为300mm=0.3m,
则圆锥的母线长为:=0.5m.
∴圆锥的侧面积=π×0.4×0.5=0.2π(m2),
∵圆柱的高为800mm=0.8m.
圆柱的侧面积=2π×0.4×0.8=0.64π(m2),
∴浮筒的表面积==2S圆锥侧面积+S圆柱侧面积,=1.04π(m2),
∵每平方米用锌0.11kg,
∴一个浮筒需用锌:1.04π×0.11kg,
∴100个这样的锚标浮筒需用锌:100×1.04π×0.11=11.44π(kg).
答:100个这样的锚标浮筒需用锌11.44πkg.
18.解:∵Rt△AOD中,AO=7﹣4=3cm,OD=4cm,
∴AD==5cm,
∴所得到的几何体的表面积为π×4×5+π×4×2×4+π×4×4=68πcm2.
故它的全面积为68πcm2.
19.解:这个圆锥的侧面积为:×12×12π=72π(cm2),
设底面圆的半径为:r,则2πr=12π,
解得:r=6.
故这个圆锥的高为:=6(cm).
20.解:(1)设圆锥的底面半径为rcm,
扇形的弧长==,
∴2πr=,
解得,r=,即圆锥的底面半径为cm;
(2)圆锥的全面积=+π×()2=cm2.
21.(1)A到BC的距离为2,BC的长度为;(2)
【解析】(1)如图,过点作于点.
在中,
.
∴点到直线的距离为2
在中,
,
.
(2)将绕线段所在直线旋转一周,所得几何体的表面积为
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知圆锥的高为4 cm,底面半径为3 cm,那么,这个圆锥的侧面展开图扇形的圆心角的度数为( );
A.180° B.200° C.216° D.225°
2.如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm2、100cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,求甲的容积为何( )
A.1280cm3 B.2560cm3 C.3200cm3 D.4000cm3
3.圆柱底面直径为2cm,高为4cm,则圆柱的侧面积为( )cm2
A.8π B.16π C.π D.2π
4.如图,圆锥体的高h=2cm,底面圆半径r=2cm,则圆锥体的全面积为( )cm2.
A.12π B.8π C.4π D.(4+4)π
5.如图,从一圆形纸片上剪出一个半径为R、圆心角为90°的扇形;和一半径为的圆,使之恰好围成如图所示的圆锥,则R与的关系为( )
A.R=2 B.R=4 C.R=2 D.R=6
6.一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的圆心角的度数是( )
A.120° B.180° C.240° D.300°
7.一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则做成这把遮阳伞需要布料的面积是( )平方米(接缝不计).
A.π B.5π C.4π D.3π
8.“赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8cm,圆柱体部分的高BC=6cm,圆锥体部分的高CD=3cm,则这个陀螺的表面积是( )
A.68πcm2 B.74πcm2 C.84πcm2 D.100πcm2
二、填空题
9.一个圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是______.
10.若一个圆锥的底面半径为1cm,它的侧面展开图的圆心角为90°,则这个圆锥的母线长为 cm.
11.设圆锥的底面半径为2,母线长为3,该圆锥的侧面积为 .
12.用一块弧长16πcm的扇形铁片,做一个高为6cm的圆锥形工件侧面(接缝忽略不计),那么这个扇形铁片的面积为 cm2.
13.如图,一把遮阳伞撑开时母线的长是3m,底面半径为2m,则做这把遮阳伞需用布料的面积是 m2.
14.如图,从直径为的圆形纸片上剪出一个圆心角为90°的扇形ABC.使点A、B、C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面半径是 .
15.圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是 .
16.如图将母线长为9的圆锥侧面展开后得到扇形的圆心角为120°,若将该扇形剪成两个同样的扇形再围成2个同样的圆锥,则新圆锥的底面半径是 .
三、解答题
17.如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:),电镀时,如果每平方米用锌,电镀100个这样的锚标浮筒,需要用多少锌?
18.如图所示,直角梯形ABCD中,AB∥DC,AB=7cm,BC=CD=4cm,以AB所在直线为轴旋转一周,得到一个几何体,求它的全面积.
19.已知圆锥的侧面展开图是一个半径为12cm,弧长为12πcm的扇形,求这个圆锥的侧面积及高.
20.一个圆锥的侧面展开图是半径为8cm,圆心角为120°的扇形,求:
(1)圆锥的底面半径;
(2)圆锥的全面积.
21.如图,已知在中,.
(1)求点到直线的距离以及的长度.
(2)将绕线段所在的直线旋转一周,求所得几何体的表面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【解析】圆锥的母线长为:
则:
解得
故选:C.
2.解:设高都为h,根据水的容积相等可列方程80×h=100×(h﹣8).解得h=40,所以甲的容积为40×80=3200,
故选:C.
3.解:π×2×4=8πcm2,故选A.
4.解:底面圆的半径为2,则底面周长=4π,
∵底面半径为2cm、高为2cm,
∴圆锥的母线长为4cm,
∴侧面面积=×4π×4=8π;
底面积为=4π,
全面积为:8π+4π=12πcm2.
故选:A.
5.B
【解析】扇形的弧长是:=,
圆的半径为r,则底面圆的周长是,
∵恰好围成如图所示的圆锥,
∴=,
∴R=4r,
故选:B.
6.解:设母线长为R,底面半径为r,
∴底面周长=2πr,底面面积=πr2,侧面面积=πrR,
∵侧面积是底面积的2倍,
∴2πr2=πrR,
∴R=2r,
设圆心角为n,
则=2πr=πR,
解得,n=180°,
故选:B.
7.解:圆锥的底面周长=2πr=2π×2=4π,
∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,
∴圆锥的侧面积=lr=×4π×2.5=5π,
故选:B.
8.解:∵底面圆的直径为8cm,高为3cm,
∴母线长为5cm,
∴其表面积=π×4×5+42π+8π×6=84πcm2,
故选:C.
9.3π
【解析】解:由题意可得,该圆锥的侧面积是×π×22=2π.该圆锥的底面的周长是2π,则底面圆半径是1,面积是π.所以该圆锥的全面积是:2π+π=3π.
故答案为:3π.
10.解:设母线长为lcm,
则=2π×1
解得:l=4.
故答案为:4.
11.解:该圆锥的侧面积=×2π×2×3=6π.
故答案为6π.
12.解:∵扇形铁片的弧长16πcm,
∴圆锥的底面周长为16πcm,
∴圆锥的底面半径==8(cm),
由勾股定理得:圆锥的母线长==10(cm),
∴扇形铁片的面积=×16π×10=80π(cm2)
故答案为:80π.
13.解:做这把遮阳伞需用布料的面积=×2π×2×3=6π(m2).
故答案为:6π.
14.解:连接BC,如图,
∵∠BAC=90°,
∴BC为⊙O的直径,即BC=8,
∴AB=BC=8,
设这个圆锥的底面半径为r,
根据题意得2πr=,
解得r=2,
即这个圆锥的底面半径为2.
故答案为2.
15.解:设圆锥的母线长为Rcm,
根据题意得2π 5=,
解得R=10.
即圆锥的母线长为10cm,
∴圆锥的高为:=5cm.
故答案为:5cm.
16.解:∵将该扇形剪成两个同样的扇形,大扇形的圆心角为120°,
∴新扇形的圆心角为60°,
∵扇形的母线长为9,
∴扇形的弧长是:=3π,
设底面半径是r,则2πr=3π,
解得:r=.
故答案为.
17.11.44πkg
【解析】解:由图形可知圆锥的底面圆的半径为400mm=0.4m,
圆锥的高为300mm=0.3m,
则圆锥的母线长为:=0.5m.
∴圆锥的侧面积=π×0.4×0.5=0.2π(m2),
∵圆柱的高为800mm=0.8m.
圆柱的侧面积=2π×0.4×0.8=0.64π(m2),
∴浮筒的表面积==2S圆锥侧面积+S圆柱侧面积,=1.04π(m2),
∵每平方米用锌0.11kg,
∴一个浮筒需用锌:1.04π×0.11kg,
∴100个这样的锚标浮筒需用锌:100×1.04π×0.11=11.44π(kg).
答:100个这样的锚标浮筒需用锌11.44πkg.
18.解:∵Rt△AOD中,AO=7﹣4=3cm,OD=4cm,
∴AD==5cm,
∴所得到的几何体的表面积为π×4×5+π×4×2×4+π×4×4=68πcm2.
故它的全面积为68πcm2.
19.解:这个圆锥的侧面积为:×12×12π=72π(cm2),
设底面圆的半径为:r,则2πr=12π,
解得:r=6.
故这个圆锥的高为:=6(cm).
20.解:(1)设圆锥的底面半径为rcm,
扇形的弧长==,
∴2πr=,
解得,r=,即圆锥的底面半径为cm;
(2)圆锥的全面积=+π×()2=cm2.
21.(1)A到BC的距离为2,BC的长度为;(2)
【解析】(1)如图,过点作于点.
在中,
.
∴点到直线的距离为2
在中,
,
.
(2)将绕线段所在直线旋转一周,所得几何体的表面积为
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
