2021--2022学年人教版八年级数学上册11.1与三角形有关的线段同步练习(word版含答案)
文档属性
| 名称 | 2021--2022学年人教版八年级数学上册11.1与三角形有关的线段同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 433.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 09:54:14 | ||
图片预览


文档简介
人教版初中数学八年级上11.1与三角形有关的线段
一、选择题
如图,为了估计池塘两岸 , 间的距离,在池塘的一侧选取点 ,测得 米, 米,那么 , 间的距离不可能是
A. 米 B. 米 C. 米 D. 米
下列说法正确的是
A.所有的等腰三角形都是锐角三角形
B.等边三角形属于等腰三角形
C.不存在既是钝角三角形又是等腰三角形的三角形
D.一个三角形里有两个锐角,则一定是锐角三角形
为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是
A.两点之间,线段最短 B.垂线段最短
C.三角形具有稳定性 D.两直线平行,内错角相等
一个三角形的两条边分别为 和 ,第三边为整数,这样的三角形有
A. 个 B. 个 C. 个 D. 个
若等腰三角形有两条边的长度为 和 ,那么此等腰三角形的周长为
A. B. C. 或 D.
如图的方格纸中,每一个小方格都是边长为 的正方形,找出格点 ,使 成为等腰三角形,这样的格点 的个数有
A. 个 B. 个 C. 个 D. 个
已知 是正整数,若一个三角形的三边长分别是 ,,,则满足条件的 的值有
A. 个 B. 个 C. 个 D. 个
已知在正方形网格中,每个小方格都是边长为 的正方形,, 两点在格点上,位置如图,点 也在格点上,且 为等腰三角形,则点 的个数为
A. B. C. D.
已知三角形的两边长分别为 和 ,则下列长度的四条线段中能作为第三边的是
A. B. C. D.
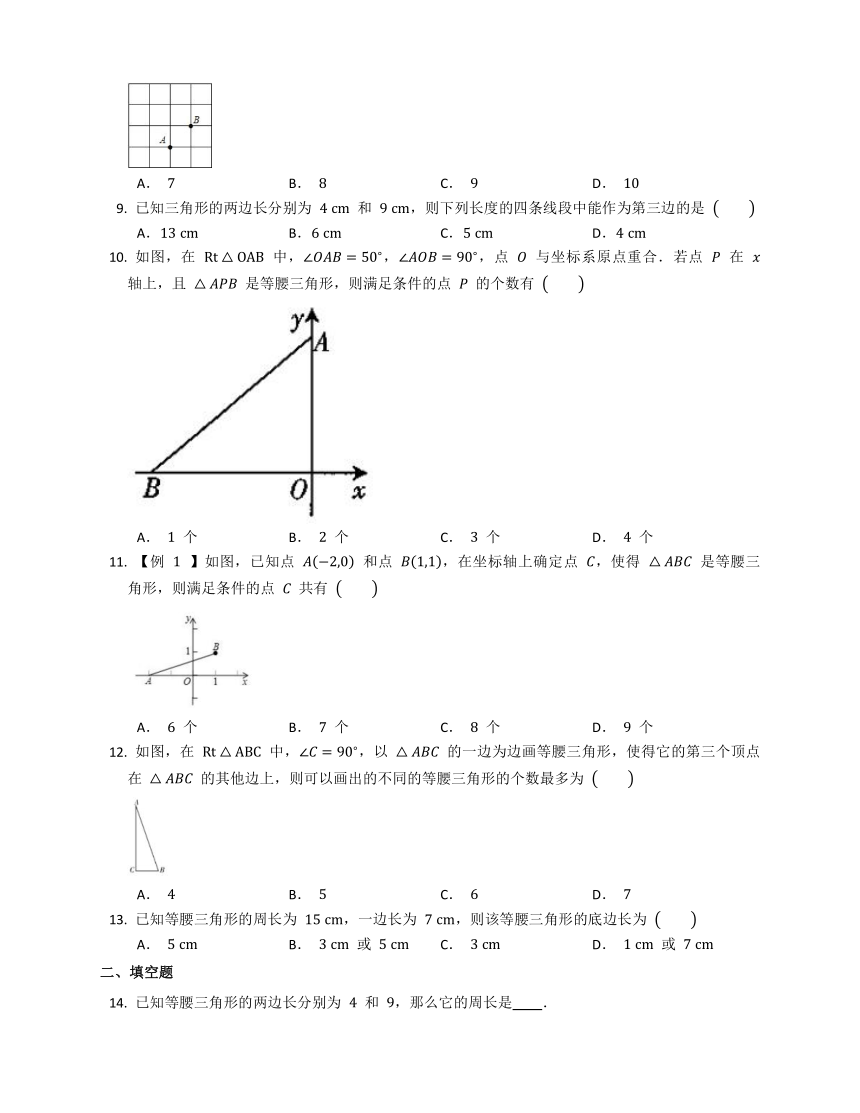
如图,在 中,,,点 与坐标系原点重合.若点 在 轴上,且 是等腰三角形,则满足条件的点 的个数有
A. 个 B. 个 C. 个 D. 个
【例 】如图,已知点 和点 ,在坐标轴上确定点 ,使得 是等腰三角形,则满足条件的点 共有
A. 个 B. 个 C. 个 D. 个
如图,在 中,,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多为
A. B. C. D.
已知等腰三角形的周长为 ,一边长为 ,则该等腰三角形的底边长为
A. B. 或 C. D. 或
二、填空题
已知等腰三角形的两边长分别为 和 ,那么它的周长是 .
阅读材料,并填表:
在 中,有一点 ,当 ,,, 没有任何三点在同一直线上时,可构成三个互不重叠的小三角形(如图),当 内点的个数增加时,若其他条件不变,请完成下表.
如图,,, 是三根长度分别为 ,, 的木棒,它们之间连接处可以活动.现在 , 之间拉一根橡皮筋,请根据四边形的不稳定性思考:
()这根橡皮筋的最大长度可以拉到 ,最短长度为 ;
()根据以上方法,若四边形的四边长分别为 ,,,,则 的取值范围是 .
如图,点 和点 在直线 的同一侧,点 到 的距离大于点 到 的距离,. 为 上一个动点,问:当点 到点 的距离与点 到点 的距离之差最大时,这个差等于 .
在三边长为自然数、周长不超过 ,最大边与最小边之和恰好等于第三边的 倍的不等边三角形中,互不全等的三角形有 个.
三、解答题
如果三角形的两边长分别为 和 ,且第三边的长为奇数,试讨论三角形的第三边应为多少?若第三边为偶数,求这个三角形的周长.
在 中,,, 分别为 的三边,且满足 ,若 的周长为 ,求 的值.
已知 ,, 是三角形的三边长,试化简:.
(1) 【问题情境】
如图 :在 中,,点 为边 上的任意一点,过点 作 ,,垂足分别为点 ,,过点 作 ,垂足为点 .求证:.
(2) 【变化一下】
()当点 在 延长线上时,请画图探究 ,, 三者之间的数量关系并给出证明;
()如图 , 满足 ,点 为 内任意一点,过点 分别作 ,,,垂足分别为点 ,,,请直接写出 ,, 和 之间的关系.
(3) 【深入探究】
如图 ,在 中,点 为 内任意一点,过点 分别作 ,,,垂足分别为点 ,,,过点 ,, 分别作 ,,,垂足分别为点 ,,,记 ,, 分别为 ,,,请直接写出 ,, 和 ,, 之间的关系.
答案
一、选择题
1.C
2.B
3.C
4.B
5.B
6.B
7.D
8.C
9.B
10.D
11.D
12.D
13.D
二、填空题
14.
15. ;
16. ; ;
17.
18.
三、解答题
19.设第三边为 ,根据三边关系,得 ,
所以 .
所以若第三边为奇数,则第三边长为 或 ;
若第三边为偶数,则第三边长为 ,
此时三角形的周长为 .
20. 的周长为 ,,
,解得 .
21. ,, 是三角形的三边长,
,,,.
.
22.
(1) 如图 中,连接 .
,
,
,
.
(2) ()如图 中,结论:.
理由:连接 .
,
,
,
.
().
(3) .
一、选择题
如图,为了估计池塘两岸 , 间的距离,在池塘的一侧选取点 ,测得 米, 米,那么 , 间的距离不可能是
A. 米 B. 米 C. 米 D. 米
下列说法正确的是
A.所有的等腰三角形都是锐角三角形
B.等边三角形属于等腰三角形
C.不存在既是钝角三角形又是等腰三角形的三角形
D.一个三角形里有两个锐角,则一定是锐角三角形
为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是
A.两点之间,线段最短 B.垂线段最短
C.三角形具有稳定性 D.两直线平行,内错角相等
一个三角形的两条边分别为 和 ,第三边为整数,这样的三角形有
A. 个 B. 个 C. 个 D. 个
若等腰三角形有两条边的长度为 和 ,那么此等腰三角形的周长为
A. B. C. 或 D.
如图的方格纸中,每一个小方格都是边长为 的正方形,找出格点 ,使 成为等腰三角形,这样的格点 的个数有
A. 个 B. 个 C. 个 D. 个
已知 是正整数,若一个三角形的三边长分别是 ,,,则满足条件的 的值有
A. 个 B. 个 C. 个 D. 个
已知在正方形网格中,每个小方格都是边长为 的正方形,, 两点在格点上,位置如图,点 也在格点上,且 为等腰三角形,则点 的个数为
A. B. C. D.
已知三角形的两边长分别为 和 ,则下列长度的四条线段中能作为第三边的是
A. B. C. D.
如图,在 中,,,点 与坐标系原点重合.若点 在 轴上,且 是等腰三角形,则满足条件的点 的个数有
A. 个 B. 个 C. 个 D. 个
【例 】如图,已知点 和点 ,在坐标轴上确定点 ,使得 是等腰三角形,则满足条件的点 共有
A. 个 B. 个 C. 个 D. 个
如图,在 中,,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多为
A. B. C. D.
已知等腰三角形的周长为 ,一边长为 ,则该等腰三角形的底边长为
A. B. 或 C. D. 或
二、填空题
已知等腰三角形的两边长分别为 和 ,那么它的周长是 .
阅读材料,并填表:
在 中,有一点 ,当 ,,, 没有任何三点在同一直线上时,可构成三个互不重叠的小三角形(如图),当 内点的个数增加时,若其他条件不变,请完成下表.
如图,,, 是三根长度分别为 ,, 的木棒,它们之间连接处可以活动.现在 , 之间拉一根橡皮筋,请根据四边形的不稳定性思考:
()这根橡皮筋的最大长度可以拉到 ,最短长度为 ;
()根据以上方法,若四边形的四边长分别为 ,,,,则 的取值范围是 .
如图,点 和点 在直线 的同一侧,点 到 的距离大于点 到 的距离,. 为 上一个动点,问:当点 到点 的距离与点 到点 的距离之差最大时,这个差等于 .
在三边长为自然数、周长不超过 ,最大边与最小边之和恰好等于第三边的 倍的不等边三角形中,互不全等的三角形有 个.
三、解答题
如果三角形的两边长分别为 和 ,且第三边的长为奇数,试讨论三角形的第三边应为多少?若第三边为偶数,求这个三角形的周长.
在 中,,, 分别为 的三边,且满足 ,若 的周长为 ,求 的值.
已知 ,, 是三角形的三边长,试化简:.
(1) 【问题情境】
如图 :在 中,,点 为边 上的任意一点,过点 作 ,,垂足分别为点 ,,过点 作 ,垂足为点 .求证:.
(2) 【变化一下】
()当点 在 延长线上时,请画图探究 ,, 三者之间的数量关系并给出证明;
()如图 , 满足 ,点 为 内任意一点,过点 分别作 ,,,垂足分别为点 ,,,请直接写出 ,, 和 之间的关系.
(3) 【深入探究】
如图 ,在 中,点 为 内任意一点,过点 分别作 ,,,垂足分别为点 ,,,过点 ,, 分别作 ,,,垂足分别为点 ,,,记 ,, 分别为 ,,,请直接写出 ,, 和 ,, 之间的关系.
答案
一、选择题
1.C
2.B
3.C
4.B
5.B
6.B
7.D
8.C
9.B
10.D
11.D
12.D
13.D
二、填空题
14.
15. ;
16. ; ;
17.
18.
三、解答题
19.设第三边为 ,根据三边关系,得 ,
所以 .
所以若第三边为奇数,则第三边长为 或 ;
若第三边为偶数,则第三边长为 ,
此时三角形的周长为 .
20. 的周长为 ,,
,解得 .
21. ,, 是三角形的三边长,
,,,.
.
22.
(1) 如图 中,连接 .
,
,
,
.
(2) ()如图 中,结论:.
理由:连接 .
,
,
,
.
().
(3) .
