2021-2022学年人教版八年级数学上册11.3多边形及其内角和 同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.3多边形及其内角和 同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 522.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 09:55:17 | ||
图片预览

文档简介
人教版初中数学八年级上:11.3多边形及其内角和
一、选择题
商店出售下列形状的地砖:①正方形;②长方形;③正五边形;④正六边形.若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有
A. 种 B. 种 C. 种 D. 种
某人到瓷砖商店购买一种多边形形状的瓷砖,用来铺设无缝地板,他购买的瓷砖形状不可以是
A.正三角形 B.矩形 C.正八边形 D.正六边形
如果一个多边形的内角和等于 ,那么这个多边形是 .
A.三角形 B.四边形 C.五边形 D.六边形
已知一个多边形的内角和是 ,则这个多边形是 .
A.五边形 B.六边形 C.七边形 D.八边形
如图,足球图片中的一块黑色皮块的内角和是
A. B. C. D.
如果一个正多边形的内角和等于 ,那么该正多边形的一个外角等于
A. B. C. D.
同学们喜欢足球吗?足球一般是用黑白两种颜色的皮块缝制而成的,如图所示,黑色皮块是正五边形、白色皮块是正六边形,若一个球上共有黑白皮块共 块,请你计算一下,黑色皮块和白线皮块的块数依次为
A. 块, 块 B. 块, 块 C. 块, 块 D. 块, 块
如图,在五边形 中,,, 分别平分 ,,则 的度数是
A. B. C. D.
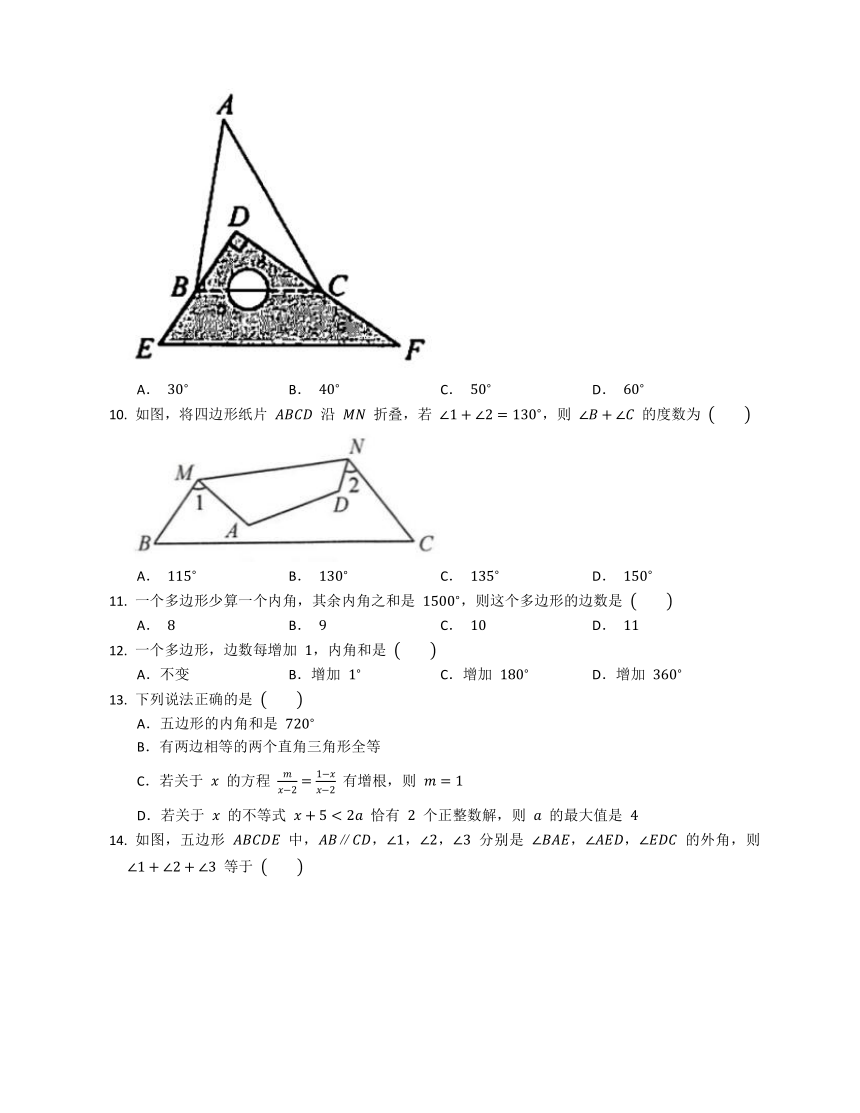
如图,将一块直角三角尺 放置在锐角 上,使得该三角板的两条直角边 , 恰好分别经过点 ,.若 ,则
A. B. C. D.
如图,将四边形纸片 沿 折叠,若 ,则 的度数为
A. B. C. D.
一个多边形少算一个内角,其余内角之和是 ,则这个多边形的边数是
A. B. C. D.
一个多边形,边数每增加 ,内角和是
A.不变 B.增加 C.增加 D.增加
下列说法正确的是
A.五边形的内角和是
B.有两边相等的两个直角三角形全等
C.若关于 的方程 有增根,则
D.若关于 的不等式 恰有 个正整数解,则 的最大值是
如图,五边形 中,,,, 分别是 ,, 的外角,则 等于
A. B. C. D.
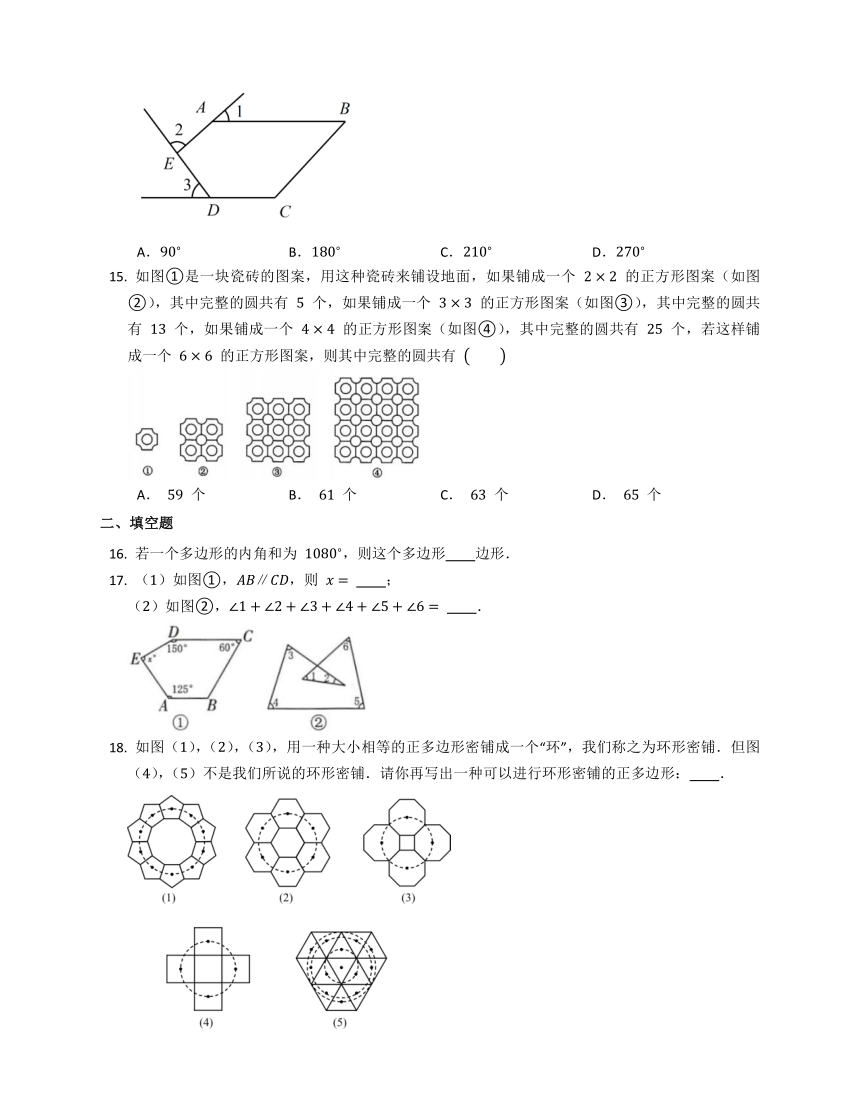
如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个 的正方形图案(如图②),其中完整的圆共有 个,如果铺成一个 的正方形图案(如图③),其中完整的圆共有 个,如果铺成一个 的正方形图案(如图④),其中完整的圆共有 个,若这样铺成一个 的正方形图案,则其中完整的圆共有
A. 个 B. 个 C. 个 D. 个
二、填空题
若一个多边形的内角和为 ,则这个多边形 边形.
()如图①,,则 ;
()如图②, .
如图(),(),(),用一种大小相等的正多边形密铺成一个“环”,我们称之为环形密铺.但图(),()不是我们所说的环形密铺.请你再写出一种可以进行环形密铺的正多边形: .
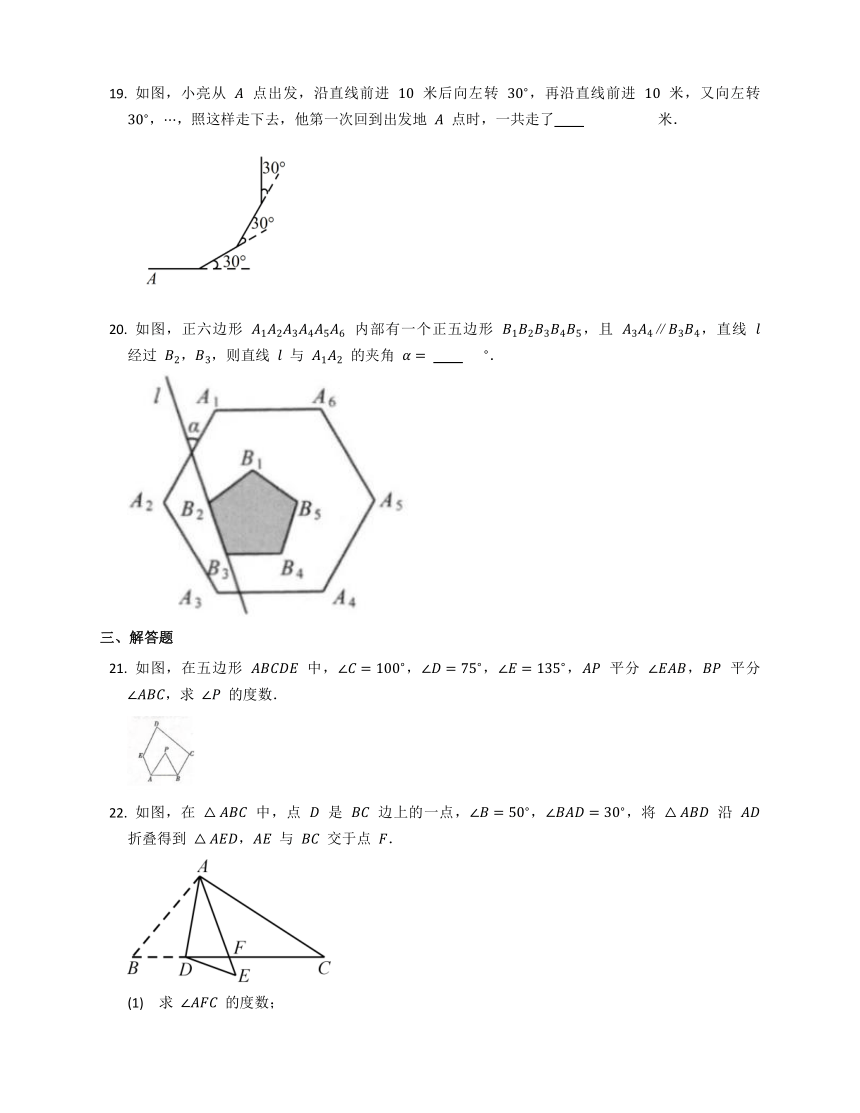
如图,小亮从 点出发,沿直线前进 米后向左转 ,再沿直线前进 米,又向左转 ,,照这样走下去,他第一次回到出发地 点时,一共走了 米.
如图,正六边形 内部有一个正五边形 ,且 ,直线 经过 ,,则直线 与 的夹角 .
三、解答题
如图,在五边形 中,,,, 平分 , 平分 ,求 的度数.
如图,在 中,点 是 边上的一点,,,将 沿 折叠得到 , 与 交于点 .
(1) 求 的度数;
(2) 求 的度数.
如图,在四边形 中,, 平分 , 平分 .
(1) 求证:;
(2) 若 ,求 的大小.
定义:每个内角都相等的八边形叫做等角八边形.容易知道,等角八边形的内角都等于 .下面,我们来研究它的一些性质与判定:
(1) 如图 ,等角八边形 中,连接 .
①请直接写出 的度数.
②求证:.
③我们把 与 称为八边形的一组正对边.由②同理可得: 与 , 与 , 与 这三组正对边也分别平行.请模仿平行四边形性质的学习经验,用一句话概括等角八边形的这一性质.
(2) 如图 ,等角八边形 中,如果有 ,,则其余两组正对边 与 , 与 分别相等吗?证明你的结论.
(3) 如图 ,八边形 中,若四组正对边分别平行,则显然有 ,,,.请探究:该八边形至少需要已知几个内角为 ,才能保证它一定是等角八边形?
答案
一、选择题
1.C
2.C
3.D
4.D
5.C
6.B
7.D
8.A
9.C
10.A
11.D
12.C
13.D
14.B
15.B
二、填空题
16.
17. ;
18.正十二边形
19.
20.
三、解答题
21.
22.
(1) 沿 折叠得到 ,
,
,,
.
(2) ,,
,,
沿 折叠得到 ,
,
.
23.
(1) ,
,
平分 , 平分 ,
,,
,
又 ,
,
.
(2) ,
,
平分 ,
.
24.
(1) ① .
② ,,
,
.
③等角八边形的每一组正对边平行.
(2) 如图 ,连接 ,,,,
由①得:,
,
四边形 是平行四边形,
,,
又 ,
,
又 ,
,
,,
,
,
又 ,
,
,.
(3) 结论:至少需要已知 个内角为 .
①若 个内角等于 ,则每个内角不一定都为 ,
反例:(数,形都可以)
如图 ,
八边形 不是等角八边形(说明略);
②若 个内角等于 :
,,,.
这八个角中,不论已知哪 个角是 ,
都可以推导出其余的内角也是 .
一、选择题
商店出售下列形状的地砖:①正方形;②长方形;③正五边形;④正六边形.若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有
A. 种 B. 种 C. 种 D. 种
某人到瓷砖商店购买一种多边形形状的瓷砖,用来铺设无缝地板,他购买的瓷砖形状不可以是
A.正三角形 B.矩形 C.正八边形 D.正六边形
如果一个多边形的内角和等于 ,那么这个多边形是 .
A.三角形 B.四边形 C.五边形 D.六边形
已知一个多边形的内角和是 ,则这个多边形是 .
A.五边形 B.六边形 C.七边形 D.八边形
如图,足球图片中的一块黑色皮块的内角和是
A. B. C. D.
如果一个正多边形的内角和等于 ,那么该正多边形的一个外角等于
A. B. C. D.
同学们喜欢足球吗?足球一般是用黑白两种颜色的皮块缝制而成的,如图所示,黑色皮块是正五边形、白色皮块是正六边形,若一个球上共有黑白皮块共 块,请你计算一下,黑色皮块和白线皮块的块数依次为
A. 块, 块 B. 块, 块 C. 块, 块 D. 块, 块
如图,在五边形 中,,, 分别平分 ,,则 的度数是
A. B. C. D.
如图,将一块直角三角尺 放置在锐角 上,使得该三角板的两条直角边 , 恰好分别经过点 ,.若 ,则
A. B. C. D.
如图,将四边形纸片 沿 折叠,若 ,则 的度数为
A. B. C. D.
一个多边形少算一个内角,其余内角之和是 ,则这个多边形的边数是
A. B. C. D.
一个多边形,边数每增加 ,内角和是
A.不变 B.增加 C.增加 D.增加
下列说法正确的是
A.五边形的内角和是
B.有两边相等的两个直角三角形全等
C.若关于 的方程 有增根,则
D.若关于 的不等式 恰有 个正整数解,则 的最大值是
如图,五边形 中,,,, 分别是 ,, 的外角,则 等于
A. B. C. D.
如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个 的正方形图案(如图②),其中完整的圆共有 个,如果铺成一个 的正方形图案(如图③),其中完整的圆共有 个,如果铺成一个 的正方形图案(如图④),其中完整的圆共有 个,若这样铺成一个 的正方形图案,则其中完整的圆共有
A. 个 B. 个 C. 个 D. 个
二、填空题
若一个多边形的内角和为 ,则这个多边形 边形.
()如图①,,则 ;
()如图②, .
如图(),(),(),用一种大小相等的正多边形密铺成一个“环”,我们称之为环形密铺.但图(),()不是我们所说的环形密铺.请你再写出一种可以进行环形密铺的正多边形: .
如图,小亮从 点出发,沿直线前进 米后向左转 ,再沿直线前进 米,又向左转 ,,照这样走下去,他第一次回到出发地 点时,一共走了 米.
如图,正六边形 内部有一个正五边形 ,且 ,直线 经过 ,,则直线 与 的夹角 .
三、解答题
如图,在五边形 中,,,, 平分 , 平分 ,求 的度数.
如图,在 中,点 是 边上的一点,,,将 沿 折叠得到 , 与 交于点 .
(1) 求 的度数;
(2) 求 的度数.
如图,在四边形 中,, 平分 , 平分 .
(1) 求证:;
(2) 若 ,求 的大小.
定义:每个内角都相等的八边形叫做等角八边形.容易知道,等角八边形的内角都等于 .下面,我们来研究它的一些性质与判定:
(1) 如图 ,等角八边形 中,连接 .
①请直接写出 的度数.
②求证:.
③我们把 与 称为八边形的一组正对边.由②同理可得: 与 , 与 , 与 这三组正对边也分别平行.请模仿平行四边形性质的学习经验,用一句话概括等角八边形的这一性质.
(2) 如图 ,等角八边形 中,如果有 ,,则其余两组正对边 与 , 与 分别相等吗?证明你的结论.
(3) 如图 ,八边形 中,若四组正对边分别平行,则显然有 ,,,.请探究:该八边形至少需要已知几个内角为 ,才能保证它一定是等角八边形?
答案
一、选择题
1.C
2.C
3.D
4.D
5.C
6.B
7.D
8.A
9.C
10.A
11.D
12.C
13.D
14.B
15.B
二、填空题
16.
17. ;
18.正十二边形
19.
20.
三、解答题
21.
22.
(1) 沿 折叠得到 ,
,
,,
.
(2) ,,
,,
沿 折叠得到 ,
,
.
23.
(1) ,
,
平分 , 平分 ,
,,
,
又 ,
,
.
(2) ,
,
平分 ,
.
24.
(1) ① .
② ,,
,
.
③等角八边形的每一组正对边平行.
(2) 如图 ,连接 ,,,,
由①得:,
,
四边形 是平行四边形,
,,
又 ,
,
又 ,
,
,,
,
,
又 ,
,
,.
(3) 结论:至少需要已知 个内角为 .
①若 个内角等于 ,则每个内角不一定都为 ,
反例:(数,形都可以)
如图 ,
八边形 不是等角八边形(说明略);
②若 个内角等于 :
,,,.
这八个角中,不论已知哪 个角是 ,
都可以推导出其余的内角也是 .
