2021-2022学年人教版九年级数学下册26.1反比例函数 同步练习 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册26.1反比例函数 同步练习 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 323.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览

文档简介
人教版初中数学九年级下:26.1反比例函数
一、选择题
正比例函数 的图象与反比例函数 的图象相交于 , 两点,其中点 的横坐标为 ,当 时, 的取值范围是
A. 或 B. 或
C. 或 D. 或
已知下列命题:
反比例函数的图象与坐标轴不相交;
反比例函数的图象位于同一坐标轴的两侧;
反比例函数 的图象,当 时, 随 的增大而增大;
反比例函数 的图象,当 时,在每个象限内, 随 的增大而增大.
其中正确的有
A. 个 B. 个 C. 个 D. 个
如图反比例函数 的图象,在某一象限内, 随 的增大而增大,那么 的取值范围在数轴上表示正确的是
A. B. C. D.
如图,已知双曲线 经过直角三角形 斜边 的中点 ,且与直角边 相交于点 .若点 的坐标为 ,则 的面积为
A. B. C. D.
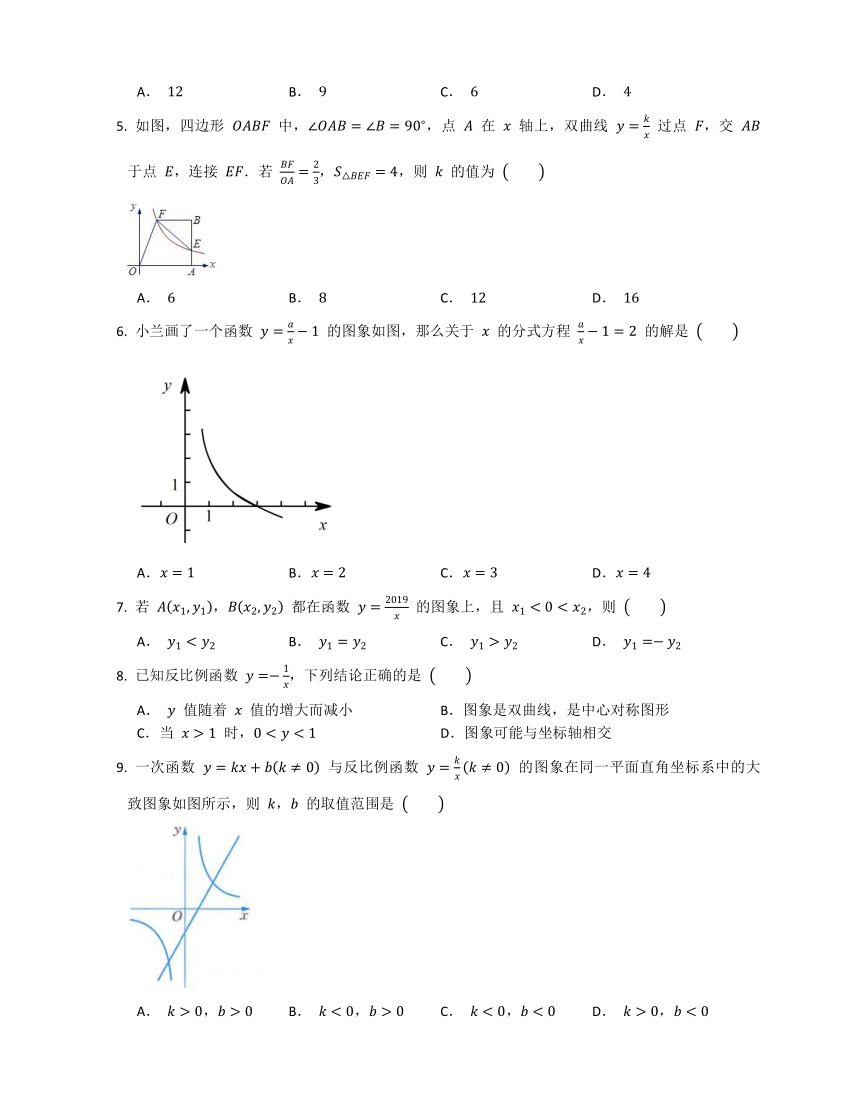
如图,四边形 中,,点 在 轴上,双曲线 过点 ,交 于点 ,连接 .若 ,,则 的值为
A. B. C. D.
小兰画了一个函数 的图象如图,那么关于 的分式方程 的解是
A. B. C. D.
若 , 都在函数 的图象上,且 ,则
A. B. C. D.
已知反比例函数 ,下列结论正确的是
A. 值随着 值的增大而减小 B.图象是双曲线,是中心对称图形
C.当 时, D.图象可能与坐标轴相交
一次函数 与反比例函数 的图象在同一平面直角坐标系中的大致图象如图所示,则 , 的取值范围是
A. , B. , C. , D. ,
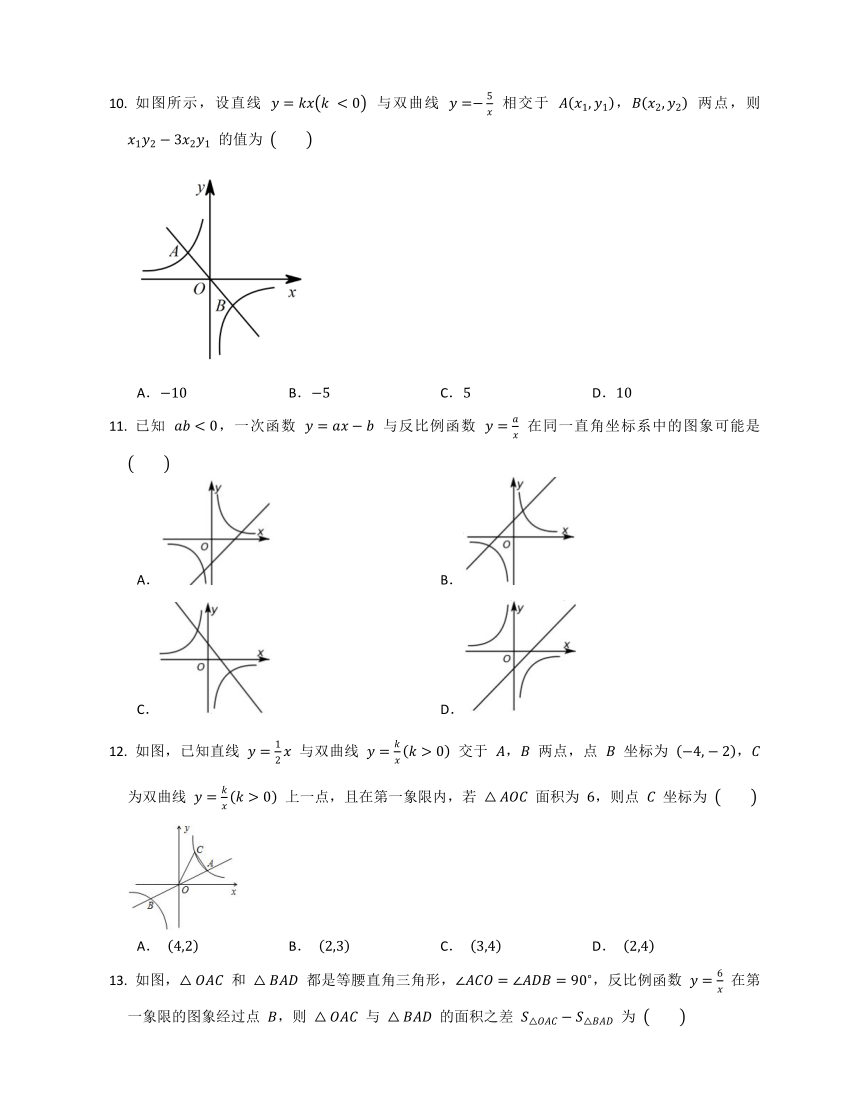
如图所示,设直线 与双曲线 相交于 , 两点,则 的值为
A. B. C. D.
已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能是
A. B.
C. D.
如图,已知直线 与双曲线 交于 , 两点,点 坐标为 , 为双曲线 上一点,且在第一象限内,若 面积为 ,则点 坐标为
A. B. C. D.
如图, 和 都是等腰直角三角形,,反比例函数 在第一象限的图象经过点 ,则 与 的面积之差 为
A. B. C. D.
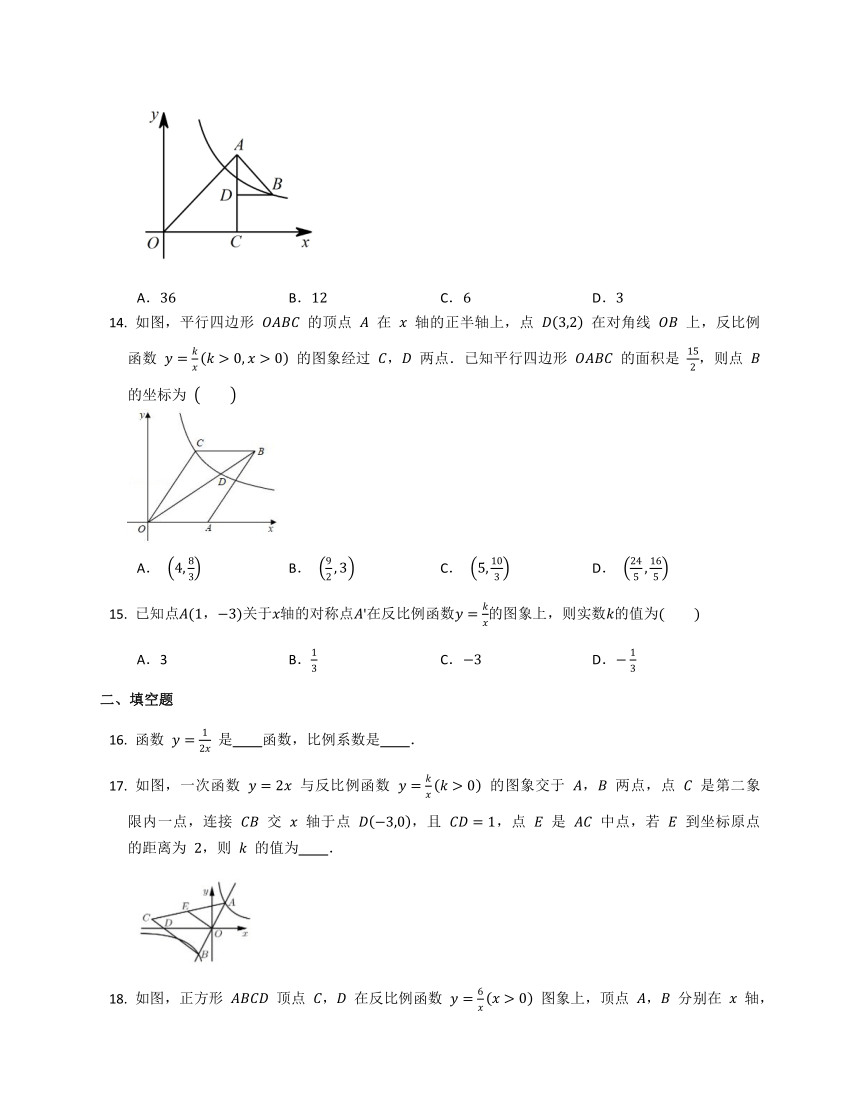
如图,平行四边形 的顶点 在 轴的正半轴上,点 在对角线 上,反比例函数 的图象经过 , 两点.已知平行四边形 的面积是 ,则点 的坐标为
A. B. C. D.
已知点,关于轴的对称点'在反比例函数的图象上,则实数的值为
A.3 B. C. D.
二、填空题
函数 是 函数,比例系数是 .
如图,一次函数 与反比例函数 的图象交于 , 两点,点 是第二象限内一点,连接 交 轴于点 ,且 ,点 是 中点,若 到坐标原点的距离为 ,则 的值为 .
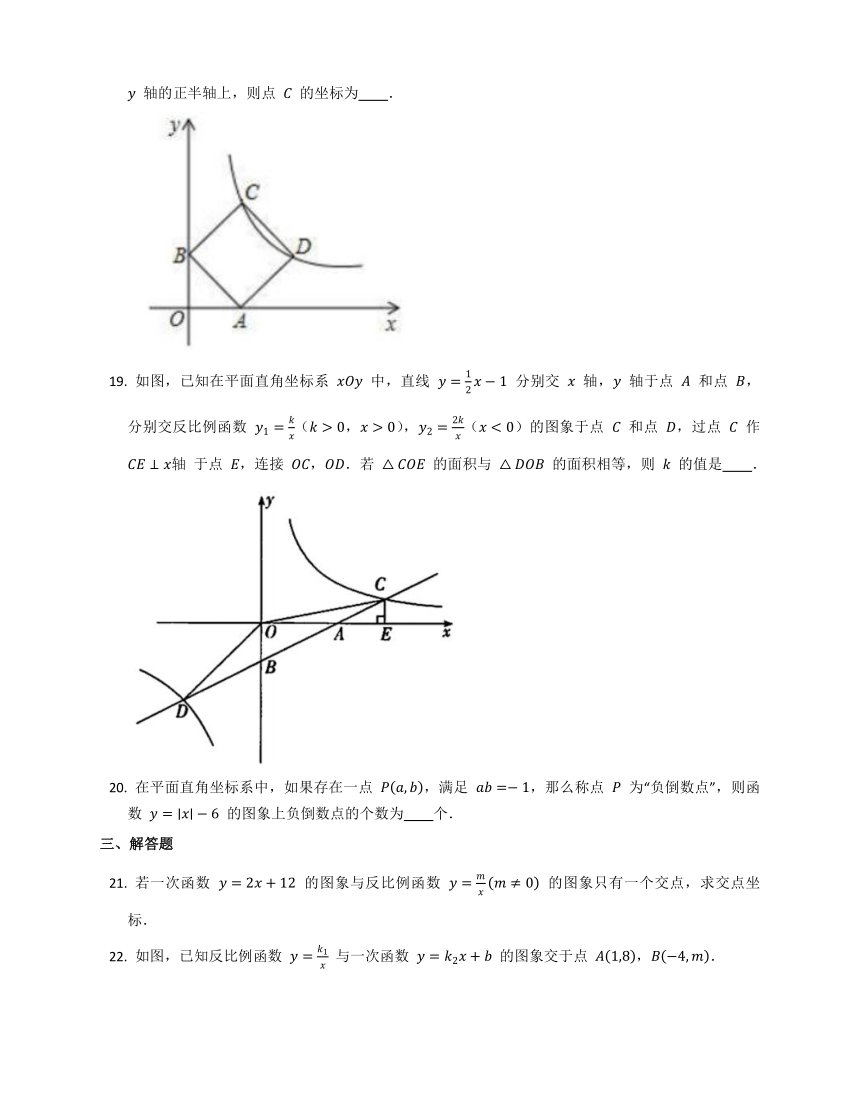
如图,正方形 顶点 , 在反比例函数 图象上,顶点 , 分别在 轴, 轴的正半轴上,则点 的坐标为 .
如图,已知在平面直角坐标系 中,直线 分别交 轴, 轴于点 和点 ,分别交反比例函数 (,),()的图象于点 和点 ,过点 作 于点 ,连接 ,.若 的面积与 的面积相等,则 的值是 .
在平面直角坐标系中,如果存在一点 ,满足 ,那么称点 为“负倒数点”,则函数 的图象上负倒数点的个数为 个.
三、解答题
若一次函数 的图象与反比例函数 的图象只有一个交点,求交点坐标.
如图,已知反比例函数 与一次函数 的图象交于点 ,.
(1) 求 ,, 的值;
(2) 求 的面积;
(3) 若 , 是比例函数 图象上的两点,且 ,,指出点 , 各位于哪个象限,并简要说明理由.
如图,在平面直角坐标系中, 为原点,, 两点分别在 轴, 轴的正半轴上, 的一条内角平分线、一条外角平分线交于点 , 在反比例函数 的图象上.
(1) 求点 的坐标;
(2) 若 ,则:
① 的度数为 ;
②求出此时直线 的函数关系式;
(3) 如果直线 的关系式为 ,且 ,作反比例函数 ,过点 作 轴的平行线与 的图象交于点 ,与 的图象交于点 ,过点 作 轴的平行线与 的图象交于点 ,若 的和始终是一个定值 ,求此时 的值及定值 .
对某一个函数给出如下定义:若存在实数 ,对于函数图象上横坐标之差为 的任意两点 ,, 都成立,则称这个函数是限减函数,在所有满足条件的 中,其最大值称为这个函数的限减系数.例如,函数 ,当 取值 和 时,函数值分别为 ,,故 ,因此函数 是限减函数,它的限减系数为 .
(1) 写出函数 的限减系数;
(2) ,已知 是限减函数,且限减系数 ,求 的取值范围;
(3) 已知函数 的图象上一点 ,过点 作直线 垂直于 轴,将函数 的图象在点 右侧的部分关于直线 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数 ,直接写出 点横坐标 的取值范围.
答案
一、选择题
1.D
2.C
3.A
4.B
5.A
6.A
7.A
8.B
9.D
10.A
11.B
12.D
13.D
14.B
15.A
二、填空题
16.反比例;
17.
18.
19.
20.
三、解答题
21. 一次函数 的图象与反比例函数 的图象只有一个交点,
只有一组解,即 有两个相等的实数根,
,
.
把 代入求得该方程的解为 ,
把 代入 ,得 ,
即所求的交点坐标为 .
22.
(1) 反比例函数 与一次函数 的图象交于点 ,,
,,
解得
(2) 由()知一次函数 的图象与 轴的交点坐标为 ,
.
(3) 反比例函数 的图象位于一、三象限,
在每个象限内, 随 的增大而减小,
,,
, 在不同的象限,
在第三象限, 在第一象限.
23.
(1) 过点 作 轴于点 ,
为 的平分线,,
.
.
设 ,
点 在反比例函数 的图象上,
,解得 (舍去负值).
.
(2) ① ;
②过 作 轴于点 ,设 交 于点 ,如图(),
, 平分 ,
.
平分 ,
.
由()知 ,
,.
.
.
,.
设直线 的解析式为 ,
则
解得
直线 的解析式为 .
(3) 依题意作图,如图(),
把 代入 中,得 ,
.
把 代入 中,得 ,
.
把 代入 中,得 ,
.
.
,
当 时, 为定值,定值 .
24.
(1) 函数 的限减系数是 .
(2) 若 ,则 , 和 是函数图象上两点,
,与函数的限减系数 不符,
所以 .
若 , 和 是函数图象上横坐标之差为 的任意两点,
则 ,,
因为 ,且 ,
所以 ,与函数的限减系数 不符.
所以 .
若 , 和 是函数图象上横坐标之差为 的任意两点,
则 ,,
因为 ,且 ,
所以 ,当 时,等号成立,
故函数的限减系数 .
所以 的取值范围是 .
(3) .
一、选择题
正比例函数 的图象与反比例函数 的图象相交于 , 两点,其中点 的横坐标为 ,当 时, 的取值范围是
A. 或 B. 或
C. 或 D. 或
已知下列命题:
反比例函数的图象与坐标轴不相交;
反比例函数的图象位于同一坐标轴的两侧;
反比例函数 的图象,当 时, 随 的增大而增大;
反比例函数 的图象,当 时,在每个象限内, 随 的增大而增大.
其中正确的有
A. 个 B. 个 C. 个 D. 个
如图反比例函数 的图象,在某一象限内, 随 的增大而增大,那么 的取值范围在数轴上表示正确的是
A. B. C. D.
如图,已知双曲线 经过直角三角形 斜边 的中点 ,且与直角边 相交于点 .若点 的坐标为 ,则 的面积为
A. B. C. D.
如图,四边形 中,,点 在 轴上,双曲线 过点 ,交 于点 ,连接 .若 ,,则 的值为
A. B. C. D.
小兰画了一个函数 的图象如图,那么关于 的分式方程 的解是
A. B. C. D.
若 , 都在函数 的图象上,且 ,则
A. B. C. D.
已知反比例函数 ,下列结论正确的是
A. 值随着 值的增大而减小 B.图象是双曲线,是中心对称图形
C.当 时, D.图象可能与坐标轴相交
一次函数 与反比例函数 的图象在同一平面直角坐标系中的大致图象如图所示,则 , 的取值范围是
A. , B. , C. , D. ,
如图所示,设直线 与双曲线 相交于 , 两点,则 的值为
A. B. C. D.
已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能是
A. B.
C. D.
如图,已知直线 与双曲线 交于 , 两点,点 坐标为 , 为双曲线 上一点,且在第一象限内,若 面积为 ,则点 坐标为
A. B. C. D.
如图, 和 都是等腰直角三角形,,反比例函数 在第一象限的图象经过点 ,则 与 的面积之差 为
A. B. C. D.
如图,平行四边形 的顶点 在 轴的正半轴上,点 在对角线 上,反比例函数 的图象经过 , 两点.已知平行四边形 的面积是 ,则点 的坐标为
A. B. C. D.
已知点,关于轴的对称点'在反比例函数的图象上,则实数的值为
A.3 B. C. D.
二、填空题
函数 是 函数,比例系数是 .
如图,一次函数 与反比例函数 的图象交于 , 两点,点 是第二象限内一点,连接 交 轴于点 ,且 ,点 是 中点,若 到坐标原点的距离为 ,则 的值为 .
如图,正方形 顶点 , 在反比例函数 图象上,顶点 , 分别在 轴, 轴的正半轴上,则点 的坐标为 .
如图,已知在平面直角坐标系 中,直线 分别交 轴, 轴于点 和点 ,分别交反比例函数 (,),()的图象于点 和点 ,过点 作 于点 ,连接 ,.若 的面积与 的面积相等,则 的值是 .
在平面直角坐标系中,如果存在一点 ,满足 ,那么称点 为“负倒数点”,则函数 的图象上负倒数点的个数为 个.
三、解答题
若一次函数 的图象与反比例函数 的图象只有一个交点,求交点坐标.
如图,已知反比例函数 与一次函数 的图象交于点 ,.
(1) 求 ,, 的值;
(2) 求 的面积;
(3) 若 , 是比例函数 图象上的两点,且 ,,指出点 , 各位于哪个象限,并简要说明理由.
如图,在平面直角坐标系中, 为原点,, 两点分别在 轴, 轴的正半轴上, 的一条内角平分线、一条外角平分线交于点 , 在反比例函数 的图象上.
(1) 求点 的坐标;
(2) 若 ,则:
① 的度数为 ;
②求出此时直线 的函数关系式;
(3) 如果直线 的关系式为 ,且 ,作反比例函数 ,过点 作 轴的平行线与 的图象交于点 ,与 的图象交于点 ,过点 作 轴的平行线与 的图象交于点 ,若 的和始终是一个定值 ,求此时 的值及定值 .
对某一个函数给出如下定义:若存在实数 ,对于函数图象上横坐标之差为 的任意两点 ,, 都成立,则称这个函数是限减函数,在所有满足条件的 中,其最大值称为这个函数的限减系数.例如,函数 ,当 取值 和 时,函数值分别为 ,,故 ,因此函数 是限减函数,它的限减系数为 .
(1) 写出函数 的限减系数;
(2) ,已知 是限减函数,且限减系数 ,求 的取值范围;
(3) 已知函数 的图象上一点 ,过点 作直线 垂直于 轴,将函数 的图象在点 右侧的部分关于直线 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数 ,直接写出 点横坐标 的取值范围.
答案
一、选择题
1.D
2.C
3.A
4.B
5.A
6.A
7.A
8.B
9.D
10.A
11.B
12.D
13.D
14.B
15.A
二、填空题
16.反比例;
17.
18.
19.
20.
三、解答题
21. 一次函数 的图象与反比例函数 的图象只有一个交点,
只有一组解,即 有两个相等的实数根,
,
.
把 代入求得该方程的解为 ,
把 代入 ,得 ,
即所求的交点坐标为 .
22.
(1) 反比例函数 与一次函数 的图象交于点 ,,
,,
解得
(2) 由()知一次函数 的图象与 轴的交点坐标为 ,
.
(3) 反比例函数 的图象位于一、三象限,
在每个象限内, 随 的增大而减小,
,,
, 在不同的象限,
在第三象限, 在第一象限.
23.
(1) 过点 作 轴于点 ,
为 的平分线,,
.
.
设 ,
点 在反比例函数 的图象上,
,解得 (舍去负值).
.
(2) ① ;
②过 作 轴于点 ,设 交 于点 ,如图(),
, 平分 ,
.
平分 ,
.
由()知 ,
,.
.
.
,.
设直线 的解析式为 ,
则
解得
直线 的解析式为 .
(3) 依题意作图,如图(),
把 代入 中,得 ,
.
把 代入 中,得 ,
.
把 代入 中,得 ,
.
.
,
当 时, 为定值,定值 .
24.
(1) 函数 的限减系数是 .
(2) 若 ,则 , 和 是函数图象上两点,
,与函数的限减系数 不符,
所以 .
若 , 和 是函数图象上横坐标之差为 的任意两点,
则 ,,
因为 ,且 ,
所以 ,与函数的限减系数 不符.
所以 .
若 , 和 是函数图象上横坐标之差为 的任意两点,
则 ,,
因为 ,且 ,
所以 ,当 时,等号成立,
故函数的限减系数 .
所以 的取值范围是 .
(3) .
