2021-2022学年九年级下册数学人教版27.2相似三角形同步习题(word版含解析)
文档属性
| 名称 | 2021-2022学年九年级下册数学人教版27.2相似三角形同步习题(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 649.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 10:06:37 | ||
图片预览


文档简介
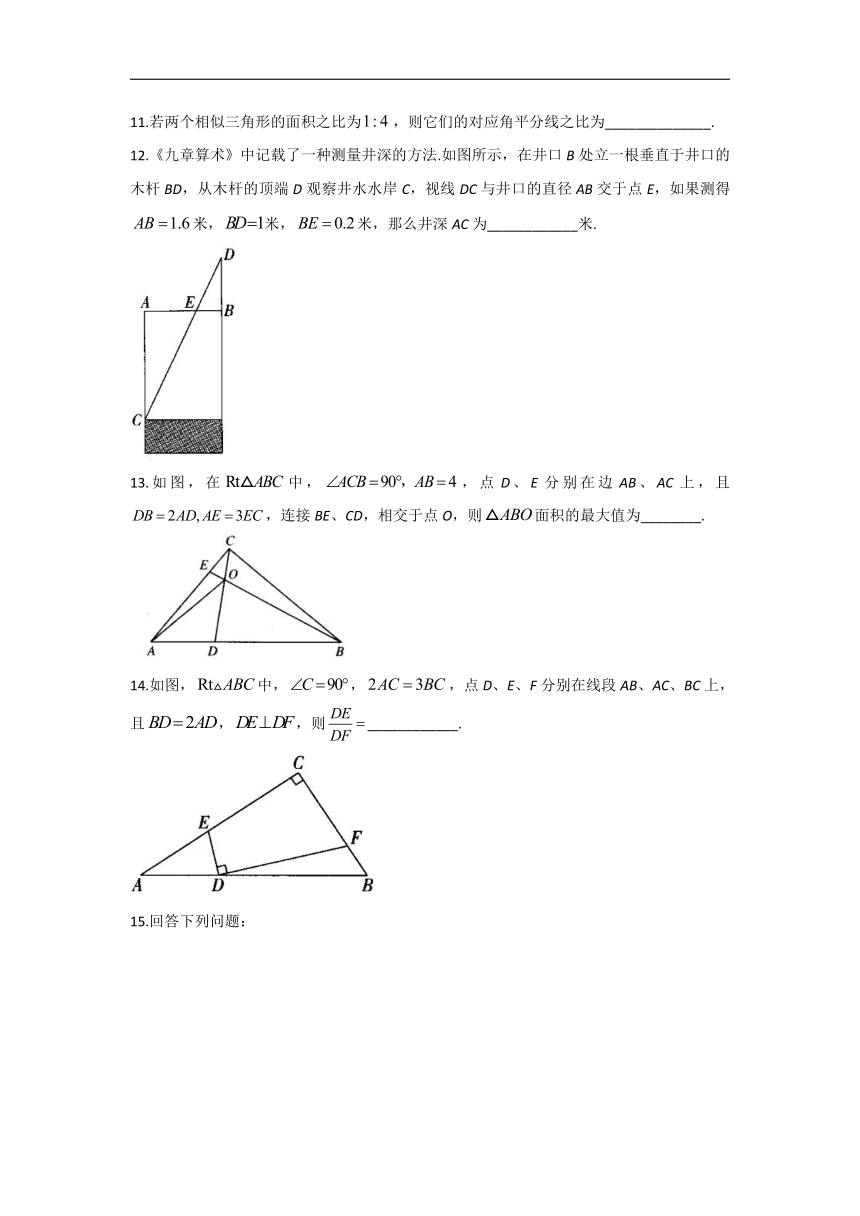
27.2相似三角形—2021-2022学年九年级数学人教版
1.下列四条线段中,为成比例线段的是( )
A.,,, B.,,,
C.,,, D.,,,
2.如图,四边形ABCD和四边形EFGH相似,则下列角的度数正确的是( )
A. B. C. D.
3.如图,在中,,,,将沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B. C. D.
4.如图,在中,E、F分别是AB、AD的中点,EF交AC于点G,则的值是( )
A. B. C. D.
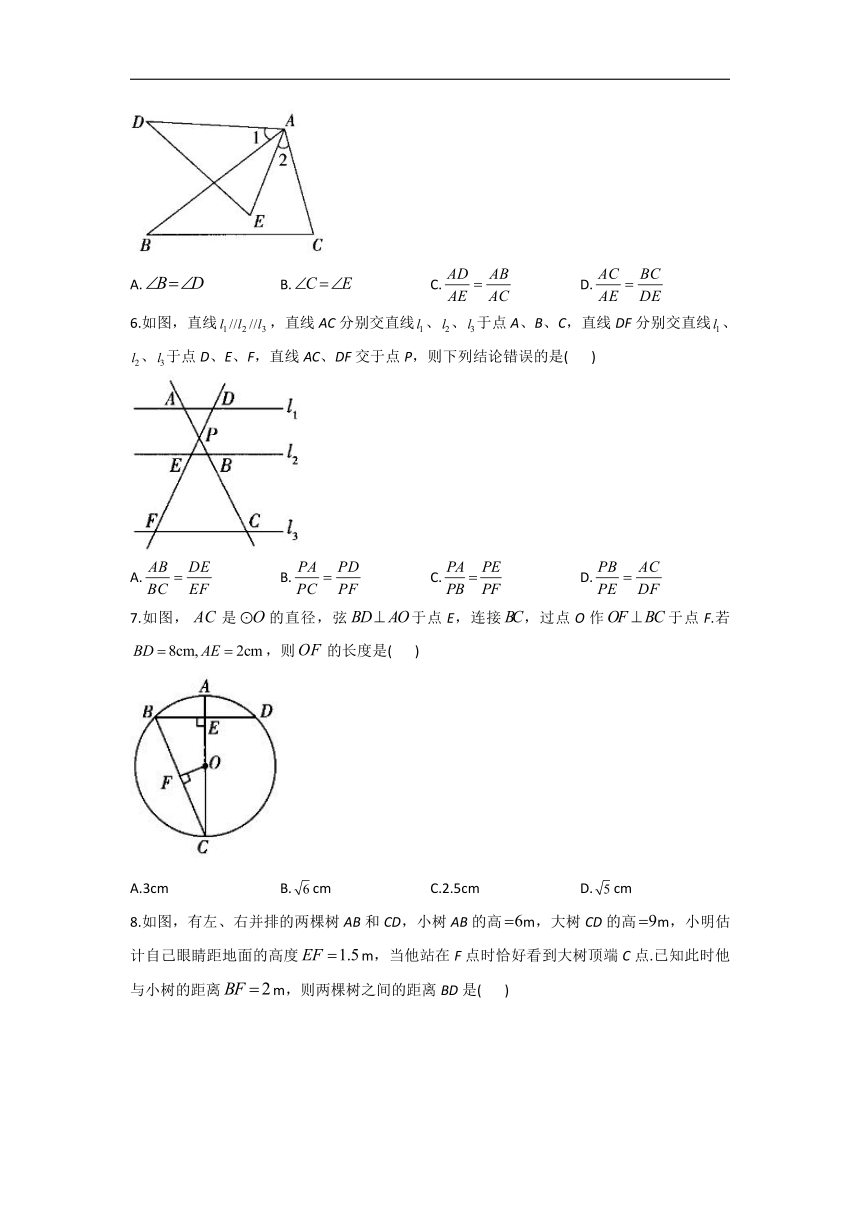
5.如图,,要使,只需要添加一个条件即可,这个条件不可能是( )
A. B. C. D.
6.如图,直线,直线AC分别交直线、、于点A、B、C,直线DF分别交直线、、于点D、E、F,直线AC、DF交于点P,则下列结论错误的是( )
A. B. C. D.
7.如图,是的直径,弦于点E,连接,过点O作于点F.若,则的长度是( )
A.3cm B.cm C.2.5cm D.cm
8.如图,有左、右并排的两棵树AB和CD,小树AB的高m,大树CD的高m,小明估计自己眼睛距地面的高度m,当他站在F点时恰好看到大树顶端C点.已知此时他与小树的距离m,则两棵树之间的距离BD是( )
A.1 m B. m C.3 m D. m
9.如图,点A在第一象限内,轴于点B,以点O为位似中心,把AB缩小为原来的得到(AB与在点O的两侧).若把点O向上平移2个单位长度,得到点,再以点为位似中心,把AB缩小为原来的得到(AB与在点的两侧),则与之间的距离为( )
A.2 B.2.5 C.3 D.4
10.如图,在中,,.正方形DEFG的顶点E,F在内,顶点D,G分别在AB,AC上,,,则点F到BC的距离为( )
A.1 B.2 C. D.
11.若两个相似三角形的面积之比为,则它们的对应角平分线之比为______________.
12.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得米,米,米,那么井深AC为____________米.
13.如图,在中,,点D、E分别在边AB、AC上,且,连接BE、CD,相交于点O,则面积的最大值为________.
14.如图,中,,,点D、E、F分别在线段AB、AC、BC上,且,,则____________.
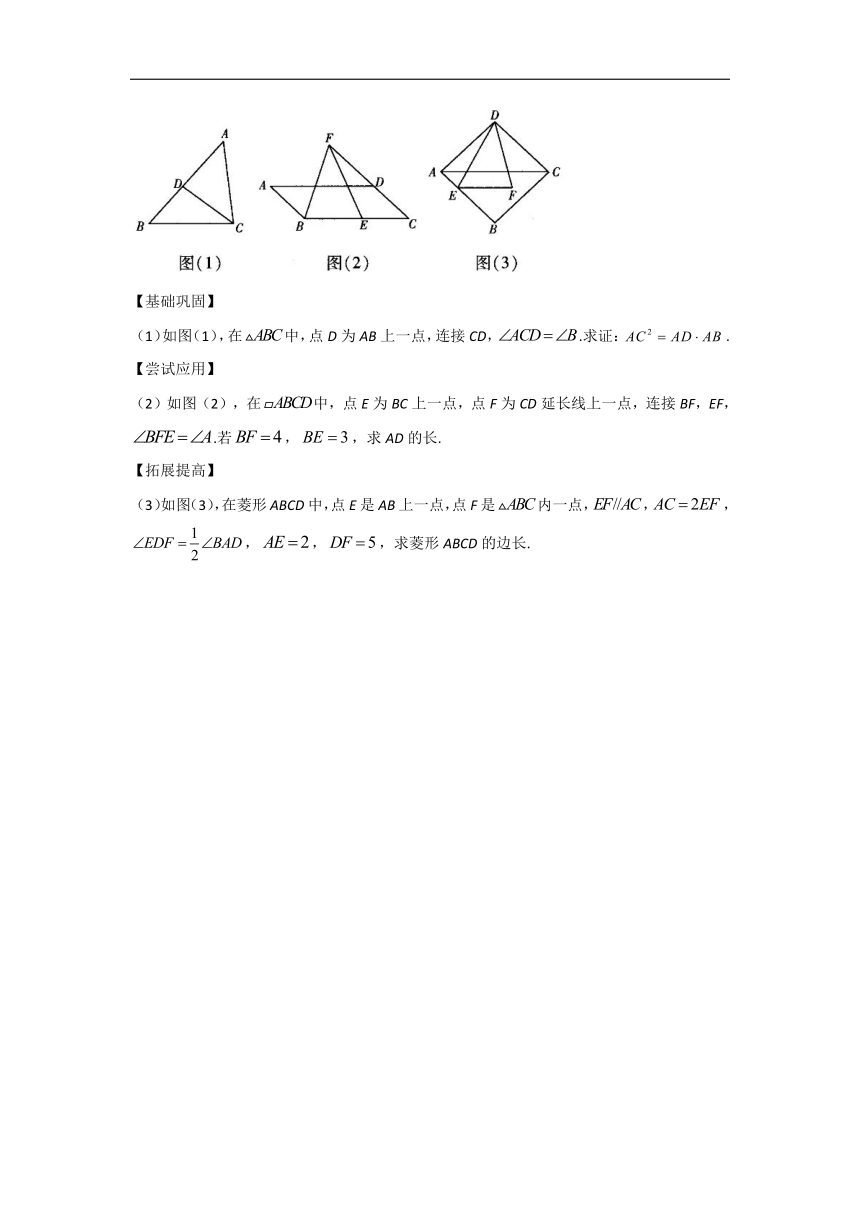
15.回答下列问题:
【基础巩固】
(1)如图(1),在中,点D为AB上一点,连接CD,.求证:.
【尝试应用】
(2)如图(2),在中,点E为BC上一点,点F为CD延长线上一点,连接BF,EF,.若,,求AD的长.
【拓展提高】
(3)如图(3),在菱形ABCD中,点E是AB上一点,点F是内一点,,,,,,求菱形ABCD的边长.
答案以及解析
1.答案:C
解析:A项,,则四条线段不成比例;B项,,则四条线段不成比例;C项,,则四条线段成比例;D项,,则四条线段不成比例.故选C.
2.答案:A
解析:四边形ABCD和四边形EFGH相似,,,,.故选A.
3.答案:B
解析:选项A,,,阴影三角形与原三角形相似,故A不合题意;选项B,且,阴影三角形与原三角形不相似,故B符合题意;选项C,,,,阴影三角形与原三角形相似,故C不合题意;选项D;,,阴影三角形与原三角形相似,故D不合题意.故选B.
4.答案:A
解析:如图,连接BD,与AC交于O,点E、F分别是AB、AD的中点, EF是的中位线,,,,,又,.故选A.
5.答案:D
解析:,,.选项A,添加,利用“两角定理”可得,故A不合题意;选项B,添加,利用“两角定理”可得,故B不合题意;选项C,添加(即),利用“两边夹角定理”可得,故C不合题意;选项D,添加,不能证明,故D符合题意.故选D.
6.答案:C
解析:,,A中结论正确,不符合题意;,B中结论正确,不符合题意;,C中结论错误,符合题意;,,D中结论正确,不符合题意.故选C.
7.答案:D
解析:如图,连接.
是的直径,弦于点,在中,,即,解得,.
在中,.
,
,即.
解得.故选D.
8.答案:B
解析:由题意,得m, m, m,m,,,,,,,即,解得m,则m.故选B.
9.答案:C
解析:如图,连接,由题意易知和都与AB平行,且在同一条直线上,.由题意知,,,.
,,,,.
10.答案:C
解析:如图,作于N,交DG于M,交EF于H.,,,,,,,,,,,,,,,,,,,易知四边形MHFG是矩形,,,点F到BC的距离为.故选C.
11.答案:
解析:两个相似三角形的面积比为,它们的对应角平分线之比为.
12.答案:7
解析:,,,,,米,米,米,,(米).
13.答案:
解析:本题考查平行线分线段成比例、三角形面积公式.如图,过点D作交BE于点F,则点C在以AB为直径的圆上,设圆心为G,当时,的面积最大,最大面积为此时面积的最大值为
14.答案:
解析:如图,过点D作于H,于G,.,,,,.,,,.,,,又,,.
15.答案:(1)证明:,,
,
,
.
(2)四边形ABCD是平行四边形,
,.
又,
.
又,
,
,
,
.
(3)如图,分别延长EF,DC相交于点G.
四边形ABCD是菱形,
,.
又,四边形AEGC为平行四边形,
,,.
,
,
.
又,
,
,
.
又,
,
.
又,
,
,
即菱形ABCD的边长为.
1.下列四条线段中,为成比例线段的是( )
A.,,, B.,,,
C.,,, D.,,,
2.如图,四边形ABCD和四边形EFGH相似,则下列角的度数正确的是( )
A. B. C. D.
3.如图,在中,,,,将沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B. C. D.
4.如图,在中,E、F分别是AB、AD的中点,EF交AC于点G,则的值是( )
A. B. C. D.
5.如图,,要使,只需要添加一个条件即可,这个条件不可能是( )
A. B. C. D.
6.如图,直线,直线AC分别交直线、、于点A、B、C,直线DF分别交直线、、于点D、E、F,直线AC、DF交于点P,则下列结论错误的是( )
A. B. C. D.
7.如图,是的直径,弦于点E,连接,过点O作于点F.若,则的长度是( )
A.3cm B.cm C.2.5cm D.cm
8.如图,有左、右并排的两棵树AB和CD,小树AB的高m,大树CD的高m,小明估计自己眼睛距地面的高度m,当他站在F点时恰好看到大树顶端C点.已知此时他与小树的距离m,则两棵树之间的距离BD是( )
A.1 m B. m C.3 m D. m
9.如图,点A在第一象限内,轴于点B,以点O为位似中心,把AB缩小为原来的得到(AB与在点O的两侧).若把点O向上平移2个单位长度,得到点,再以点为位似中心,把AB缩小为原来的得到(AB与在点的两侧),则与之间的距离为( )
A.2 B.2.5 C.3 D.4
10.如图,在中,,.正方形DEFG的顶点E,F在内,顶点D,G分别在AB,AC上,,,则点F到BC的距离为( )
A.1 B.2 C. D.
11.若两个相似三角形的面积之比为,则它们的对应角平分线之比为______________.
12.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得米,米,米,那么井深AC为____________米.
13.如图,在中,,点D、E分别在边AB、AC上,且,连接BE、CD,相交于点O,则面积的最大值为________.
14.如图,中,,,点D、E、F分别在线段AB、AC、BC上,且,,则____________.
15.回答下列问题:
【基础巩固】
(1)如图(1),在中,点D为AB上一点,连接CD,.求证:.
【尝试应用】
(2)如图(2),在中,点E为BC上一点,点F为CD延长线上一点,连接BF,EF,.若,,求AD的长.
【拓展提高】
(3)如图(3),在菱形ABCD中,点E是AB上一点,点F是内一点,,,,,,求菱形ABCD的边长.
答案以及解析
1.答案:C
解析:A项,,则四条线段不成比例;B项,,则四条线段不成比例;C项,,则四条线段成比例;D项,,则四条线段不成比例.故选C.
2.答案:A
解析:四边形ABCD和四边形EFGH相似,,,,.故选A.
3.答案:B
解析:选项A,,,阴影三角形与原三角形相似,故A不合题意;选项B,且,阴影三角形与原三角形不相似,故B符合题意;选项C,,,,阴影三角形与原三角形相似,故C不合题意;选项D;,,阴影三角形与原三角形相似,故D不合题意.故选B.
4.答案:A
解析:如图,连接BD,与AC交于O,点E、F分别是AB、AD的中点, EF是的中位线,,,,,又,.故选A.
5.答案:D
解析:,,.选项A,添加,利用“两角定理”可得,故A不合题意;选项B,添加,利用“两角定理”可得,故B不合题意;选项C,添加(即),利用“两边夹角定理”可得,故C不合题意;选项D,添加,不能证明,故D符合题意.故选D.
6.答案:C
解析:,,A中结论正确,不符合题意;,B中结论正确,不符合题意;,C中结论错误,符合题意;,,D中结论正确,不符合题意.故选C.
7.答案:D
解析:如图,连接.
是的直径,弦于点,在中,,即,解得,.
在中,.
,
,即.
解得.故选D.
8.答案:B
解析:由题意,得m, m, m,m,,,,,,,即,解得m,则m.故选B.
9.答案:C
解析:如图,连接,由题意易知和都与AB平行,且在同一条直线上,.由题意知,,,.
,,,,.
10.答案:C
解析:如图,作于N,交DG于M,交EF于H.,,,,,,,,,,,,,,,,,,,易知四边形MHFG是矩形,,,点F到BC的距离为.故选C.
11.答案:
解析:两个相似三角形的面积比为,它们的对应角平分线之比为.
12.答案:7
解析:,,,,,米,米,米,,(米).
13.答案:
解析:本题考查平行线分线段成比例、三角形面积公式.如图,过点D作交BE于点F,则点C在以AB为直径的圆上,设圆心为G,当时,的面积最大,最大面积为此时面积的最大值为
14.答案:
解析:如图,过点D作于H,于G,.,,,,.,,,.,,,又,,.
15.答案:(1)证明:,,
,
,
.
(2)四边形ABCD是平行四边形,
,.
又,
.
又,
,
,
,
.
(3)如图,分别延长EF,DC相交于点G.
四边形ABCD是菱形,
,.
又,四边形AEGC为平行四边形,
,,.
,
,
.
又,
,
,
.
又,
,
.
又,
,
,
即菱形ABCD的边长为.
