2021-2022学年人教版九年级数学下册 27.2相似三角形 期末复习自主提升训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册 27.2相似三角形 期末复习自主提升训练(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 246.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学下册《27.2相似三角形》期末复习自主提升训练(附答案)
1.一个四边形的各边之比为1:2:3:4,和它相似的另一个四边形的最小边长为5cm,则它的最大边长为( )
A.10cm B.15cm C.20cm D.25cm
2.两个相似的六边形,如果一组对应边的长分别为3cm,4cm,且它们面积的差为28cm2,则较大的六边形的面积为( )
A.44.8 cm2 B.45 cm2 C.64 cm2 D.54 cm2
3.如果两个相似三角形的相似比为2:3,那么这两个三角形的面积比为( )
A.2:3 B. C.4:9 D.9:4
4.若两个三角形的相似比为1:2,则它们的面积比为( )
A.1:2 B.1:4 C.2:1 D.4:1
5.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A.B.C.D.
6.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.在△ABC内并排(不重叠)放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放( )个小正方形纸片.
A.14个 B.15个 C.16个 D.17个
7.如图,有一块锐角三角形材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使其一边在BC上,其余两个顶点分别在AB、AC上,则这个正方形零件的边长为( )
A.40mm B.45mm C.48mm D.60mm
8.如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DC=4,BC=9,则AC为( )
A.5 B.6 C.7 D.8
9.把一个正多边形的边长放大到原来的3倍,则原图形与新图形的面积比为 .
10.如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为,连接CF,则CF= .
11.如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,点A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣3x﹣8,AB为半圆的直径,点M为半圆的圆心,点P为x轴正半轴上的一点,若△COP∽△CPD,则点P的坐标是 .
12.如图,若不增加字母与辅助线,要得到△ABC∽△ADE,只需要再添加一个条件是 .
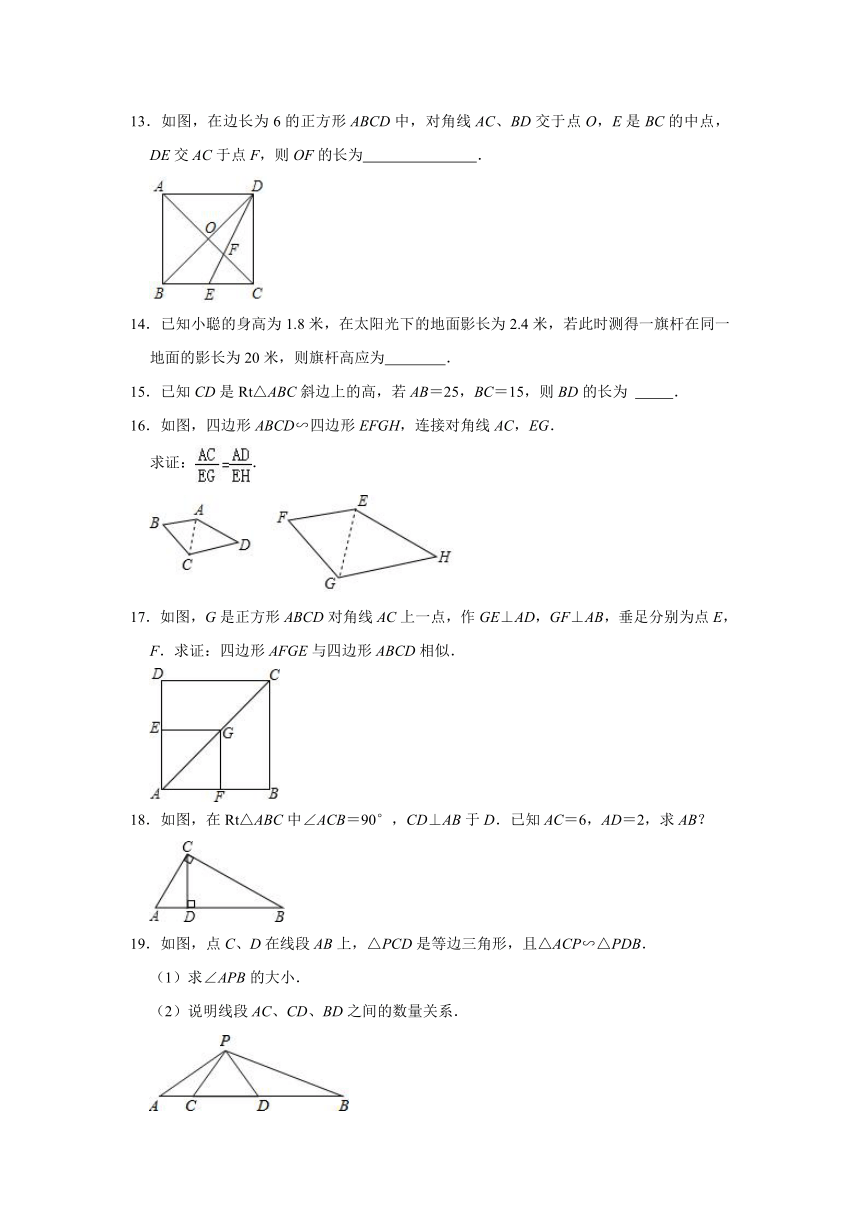
13.如图,在边长为6的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则OF的长为 .
14.已知小聪的身高为1.8米,在太阳光下的地面影长为2.4米,若此时测得一旗杆在同一地面的影长为20米,则旗杆高应为 .
15.已知CD是Rt△ABC斜边上的高,若AB=25,BC=15,则BD的长为 .
16.如图,四边形ABCD∽四边形EFGH,连接对角线AC,EG.
求证:.
17.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
18.如图,在Rt△ABC中∠ACB=90°,CD⊥AB于D.已知AC=6,AD=2,求AB?
19.如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
(1)求∠APB的大小.
(2)说明线段AC、CD、BD之间的数量关系.
20.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
21.一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
22.如图,在四边形ABCD中,AC平分∠DAB,AC2=AB AD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)CE与AD有怎样的位置关系?试说明理由.
(3)若AD=4,AB=6,求的值.
23.如图所示,在边长为1个单位长度的小正方形组成的网格中,△ABC是格点三角形(三角形的顶点是网格线的交点).
(1)画一个格点△DEF,使△DEF与△ABC相似;
(2)运用所学知识证明△DEF与△ABC相似.
参考答案
1.解:设它的最大边长为xcm,
∵两个四边形相似,
∴=,
解得,x=20,
故选:C.
2.解:设大六边形的面积为xcm2,则小六边形的面积为(x﹣28)cm2,
∵两个六边形相似,
∴=()2,
解得,x=64,
故选:C.
3.解:∵两个相似三角形的相似比为2:3,
∴这两个三角形的面积比为4:9,
故选:C.
4.解:∵两个三角形的相似比为1:2,
∴它们的面积比为1:4,
故选:B.
5.解:根据题意得:AB==,AC=2,BC==,
∴BC:AC:AB=1::,
A、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;
B、三边之比::3,图中的三角形(阴影部分)与△ABC不相似;
C、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:A.
6.解:作CF⊥AB于点F.
在Rt△ABC中,∠C=90°,AC=8,BC=6,则由勾股定理,得AB=10
∵S△ABC=AB CF=AC BC
∴CF=4.8.
则小正方形可以排4排.
最下边的一排小正方形的上边的边所在的直线与△ABC的边交于D、E.
∵DE∥AB,
=,=,
解得:DE=整数部分是7.
则最下边一排是7个正方形.
第二排正方形的上边的边所在的直线与△ABC的边交于G、H.
=,
解得GH=整数部分是5,
则第二排是5个正方形;
同理:第三排是:3个;
第四排是:1个.
则正方形的个数是:7+5+3+1=16.
故选:C.
7.解:设正方形的边长为xmm,
则AK=AD﹣x=80﹣x,
∵四边形EFGH是正方形,
∴EH∥FG,
∴△AEH∽△ABC,
∴=,
即=,
解得x=48mm,
故选:C.
8.解:由射影定理得,
AC2=CD CB=4×9=36,
∴AC=6.
故选:B.
9.解:把一个正多边形的边长放大到原来的3倍,
则原图形与新图形的相似比为1:3,
∴原图形与新图形的面积比为1:9,
故答案为:1:9.
10.解:延长GF交BC于M,
∵四边形AEFG和ABCD是矩形,
∴GF∥AE,
∵AB⊥BC,
∴GM⊥BC,
分两种情况:
①当AD与AG对应时,
∵相似比为,
∴,
∵AB=12,AD=BC=9,
∴EF=AG=BM=6,GF=AE=8,
∴FM=12﹣8=4,CM=9﹣6=3,
在Rt△CMF中,由勾股定理得:CF==5,
②当AD与AE对应时,
∵相似比为,
∴,
∴,
∴AG=8,AE=6,
∴FM=12﹣6=6,CM=9﹣8=1,
在Rt△CMF中,由勾股定理得:CF==,
故答案为:5或.
11.解:如图所示,连接CM,
令y=0,则x2﹣3x﹣8=0,
解得x1=﹣2,x2=8,
∴AO=2,BO=8,
∴AB=10,CM=5,OM=3,
∴Rt△COM中,OC=4,
令x=0,则y=﹣8,
∴OD=8,
若△COP∽△CPD,则∠COP=∠CPD=90°,
又∵OP⊥CD,
∴OP2=CO×OD,
即OP==4,
又∵点P为x轴正半轴上的一点,
∴点P的坐标为(4,0),
故答案为:(4,0).
12.解:由图可得,∠BAC=∠DAE,根据三角形的判定:两角对应相等,两三角形相似.
可添加条件:DE∥BC,则∠ABC=∠ADE,
则△ADE∽△ABC,
故答案为:DE∥BC(答案不唯一).
13.解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC=6,
∴AC==6,
∴OA=OC=3,
∵AD∥BC,
∴△AFD∽△CFE,
∴==2,
∴CF=AC=2,
∴OF=OC﹣CF=,
故答案为:.
14.解:设旗杆高为xm,
根据题意得,=,
解得x=15m.
故答案为:15.
15.解:由射影定理得,BC2=BD AB,
则BD==9,
故答案为:9.
16.证明:∵四边形ABCD∽四边形EFGH,
∴=,∠D=∠H,
∴△ADC∽△EHG,
∴.
17.证明;∵∠GEA=∠EAF=∠GFA=90°,
∴四边形EAFG为矩形.
∵四边形ABCD为正方形,
∴AC平分∠DAB.
又∵GE⊥AD,GF⊥AB,
∴GE=GF.
∴四边形EAFG为正方形.
∴四边形AFGE与四边形ABCD相似.
18.解:∵∠ACB=90°,CD⊥AB,
∴AC2=AD AB,又AC=6,AD=2,
∴AB=18.
19.解:(1)∵△PCD是等边三角形,
∴∠PCD=60°,
∴∠A+∠APC=60°,
∵△ACP∽△PDB,
∴∠APC=∠PBD,
∴∠A+∠B=60°,
∴∠APB=120°;
(2)∵△ACP∽△PDB,
∴=,
∴CD2=AC BD.
20.(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)答:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC﹣∠BAD=∠CBA﹣∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
21.解:如图所示
∵四边形PQMN是矩形,
∴BC∥PQ,
∴△APQ∽△ABC,
∴,
由于矩形长与宽的比为3:2,
∴分两种情况:
①若PQ为长,PN为宽,
设PQ=3k,PN=2k,
则,
解得:k=2,
∴PQ=6cm,PN=4cm;
②PN为6,PQ为宽,
设PN=3k,PQ=2k,
则,
解得:k=,
∴PN=cm,PQ=cm;
综上所述:矩形的长为6cm,宽为4cm;或长为cm,宽为cm.
22.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵AC2=AB AD,
∴=,
∴△ADC∽△ACB;
(2)CE∥AD,
理由如下:∵△ADC∽△ACB,
∴∠ACB=∠ADC=90°,
∵点E为AB的中点,
∴CE=AE=AB,
∴∠EAC=∠ECA,
∴∠DAC=∠EAC,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)由(2)得,CE=AB=3,
∵CE∥AD,
∴==,
∴=.
23.解:(1)如图所示,△DEF即为所求;
(2)证明:由勾股定理可得,AB=,AC=,DE=2,DF=2,
又∵BC=2,EF=4,
∴===,
∴△ABC∽△DEF.
1.一个四边形的各边之比为1:2:3:4,和它相似的另一个四边形的最小边长为5cm,则它的最大边长为( )
A.10cm B.15cm C.20cm D.25cm
2.两个相似的六边形,如果一组对应边的长分别为3cm,4cm,且它们面积的差为28cm2,则较大的六边形的面积为( )
A.44.8 cm2 B.45 cm2 C.64 cm2 D.54 cm2
3.如果两个相似三角形的相似比为2:3,那么这两个三角形的面积比为( )
A.2:3 B. C.4:9 D.9:4
4.若两个三角形的相似比为1:2,则它们的面积比为( )
A.1:2 B.1:4 C.2:1 D.4:1
5.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A.B.C.D.
6.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.在△ABC内并排(不重叠)放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放( )个小正方形纸片.
A.14个 B.15个 C.16个 D.17个
7.如图,有一块锐角三角形材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使其一边在BC上,其余两个顶点分别在AB、AC上,则这个正方形零件的边长为( )
A.40mm B.45mm C.48mm D.60mm
8.如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DC=4,BC=9,则AC为( )
A.5 B.6 C.7 D.8
9.把一个正多边形的边长放大到原来的3倍,则原图形与新图形的面积比为 .
10.如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为,连接CF,则CF= .
11.如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,点A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣3x﹣8,AB为半圆的直径,点M为半圆的圆心,点P为x轴正半轴上的一点,若△COP∽△CPD,则点P的坐标是 .
12.如图,若不增加字母与辅助线,要得到△ABC∽△ADE,只需要再添加一个条件是 .
13.如图,在边长为6的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则OF的长为 .
14.已知小聪的身高为1.8米,在太阳光下的地面影长为2.4米,若此时测得一旗杆在同一地面的影长为20米,则旗杆高应为 .
15.已知CD是Rt△ABC斜边上的高,若AB=25,BC=15,则BD的长为 .
16.如图,四边形ABCD∽四边形EFGH,连接对角线AC,EG.
求证:.
17.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
18.如图,在Rt△ABC中∠ACB=90°,CD⊥AB于D.已知AC=6,AD=2,求AB?
19.如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
(1)求∠APB的大小.
(2)说明线段AC、CD、BD之间的数量关系.
20.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
21.一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
22.如图,在四边形ABCD中,AC平分∠DAB,AC2=AB AD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)CE与AD有怎样的位置关系?试说明理由.
(3)若AD=4,AB=6,求的值.
23.如图所示,在边长为1个单位长度的小正方形组成的网格中,△ABC是格点三角形(三角形的顶点是网格线的交点).
(1)画一个格点△DEF,使△DEF与△ABC相似;
(2)运用所学知识证明△DEF与△ABC相似.
参考答案
1.解:设它的最大边长为xcm,
∵两个四边形相似,
∴=,
解得,x=20,
故选:C.
2.解:设大六边形的面积为xcm2,则小六边形的面积为(x﹣28)cm2,
∵两个六边形相似,
∴=()2,
解得,x=64,
故选:C.
3.解:∵两个相似三角形的相似比为2:3,
∴这两个三角形的面积比为4:9,
故选:C.
4.解:∵两个三角形的相似比为1:2,
∴它们的面积比为1:4,
故选:B.
5.解:根据题意得:AB==,AC=2,BC==,
∴BC:AC:AB=1::,
A、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;
B、三边之比::3,图中的三角形(阴影部分)与△ABC不相似;
C、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:A.
6.解:作CF⊥AB于点F.
在Rt△ABC中,∠C=90°,AC=8,BC=6,则由勾股定理,得AB=10
∵S△ABC=AB CF=AC BC
∴CF=4.8.
则小正方形可以排4排.
最下边的一排小正方形的上边的边所在的直线与△ABC的边交于D、E.
∵DE∥AB,
=,=,
解得:DE=整数部分是7.
则最下边一排是7个正方形.
第二排正方形的上边的边所在的直线与△ABC的边交于G、H.
=,
解得GH=整数部分是5,
则第二排是5个正方形;
同理:第三排是:3个;
第四排是:1个.
则正方形的个数是:7+5+3+1=16.
故选:C.
7.解:设正方形的边长为xmm,
则AK=AD﹣x=80﹣x,
∵四边形EFGH是正方形,
∴EH∥FG,
∴△AEH∽△ABC,
∴=,
即=,
解得x=48mm,
故选:C.
8.解:由射影定理得,
AC2=CD CB=4×9=36,
∴AC=6.
故选:B.
9.解:把一个正多边形的边长放大到原来的3倍,
则原图形与新图形的相似比为1:3,
∴原图形与新图形的面积比为1:9,
故答案为:1:9.
10.解:延长GF交BC于M,
∵四边形AEFG和ABCD是矩形,
∴GF∥AE,
∵AB⊥BC,
∴GM⊥BC,
分两种情况:
①当AD与AG对应时,
∵相似比为,
∴,
∵AB=12,AD=BC=9,
∴EF=AG=BM=6,GF=AE=8,
∴FM=12﹣8=4,CM=9﹣6=3,
在Rt△CMF中,由勾股定理得:CF==5,
②当AD与AE对应时,
∵相似比为,
∴,
∴,
∴AG=8,AE=6,
∴FM=12﹣6=6,CM=9﹣8=1,
在Rt△CMF中,由勾股定理得:CF==,
故答案为:5或.
11.解:如图所示,连接CM,
令y=0,则x2﹣3x﹣8=0,
解得x1=﹣2,x2=8,
∴AO=2,BO=8,
∴AB=10,CM=5,OM=3,
∴Rt△COM中,OC=4,
令x=0,则y=﹣8,
∴OD=8,
若△COP∽△CPD,则∠COP=∠CPD=90°,
又∵OP⊥CD,
∴OP2=CO×OD,
即OP==4,
又∵点P为x轴正半轴上的一点,
∴点P的坐标为(4,0),
故答案为:(4,0).
12.解:由图可得,∠BAC=∠DAE,根据三角形的判定:两角对应相等,两三角形相似.
可添加条件:DE∥BC,则∠ABC=∠ADE,
则△ADE∽△ABC,
故答案为:DE∥BC(答案不唯一).
13.解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC=6,
∴AC==6,
∴OA=OC=3,
∵AD∥BC,
∴△AFD∽△CFE,
∴==2,
∴CF=AC=2,
∴OF=OC﹣CF=,
故答案为:.
14.解:设旗杆高为xm,
根据题意得,=,
解得x=15m.
故答案为:15.
15.解:由射影定理得,BC2=BD AB,
则BD==9,
故答案为:9.
16.证明:∵四边形ABCD∽四边形EFGH,
∴=,∠D=∠H,
∴△ADC∽△EHG,
∴.
17.证明;∵∠GEA=∠EAF=∠GFA=90°,
∴四边形EAFG为矩形.
∵四边形ABCD为正方形,
∴AC平分∠DAB.
又∵GE⊥AD,GF⊥AB,
∴GE=GF.
∴四边形EAFG为正方形.
∴四边形AFGE与四边形ABCD相似.
18.解:∵∠ACB=90°,CD⊥AB,
∴AC2=AD AB,又AC=6,AD=2,
∴AB=18.
19.解:(1)∵△PCD是等边三角形,
∴∠PCD=60°,
∴∠A+∠APC=60°,
∵△ACP∽△PDB,
∴∠APC=∠PBD,
∴∠A+∠B=60°,
∴∠APB=120°;
(2)∵△ACP∽△PDB,
∴=,
∴CD2=AC BD.
20.(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)答:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC﹣∠BAD=∠CBA﹣∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
21.解:如图所示
∵四边形PQMN是矩形,
∴BC∥PQ,
∴△APQ∽△ABC,
∴,
由于矩形长与宽的比为3:2,
∴分两种情况:
①若PQ为长,PN为宽,
设PQ=3k,PN=2k,
则,
解得:k=2,
∴PQ=6cm,PN=4cm;
②PN为6,PQ为宽,
设PN=3k,PQ=2k,
则,
解得:k=,
∴PN=cm,PQ=cm;
综上所述:矩形的长为6cm,宽为4cm;或长为cm,宽为cm.
22.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵AC2=AB AD,
∴=,
∴△ADC∽△ACB;
(2)CE∥AD,
理由如下:∵△ADC∽△ACB,
∴∠ACB=∠ADC=90°,
∵点E为AB的中点,
∴CE=AE=AB,
∴∠EAC=∠ECA,
∴∠DAC=∠EAC,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)由(2)得,CE=AB=3,
∵CE∥AD,
∴==,
∴=.
23.解:(1)如图所示,△DEF即为所求;
(2)证明:由勾股定理可得,AB=,AC=,DE=2,DF=2,
又∵BC=2,EF=4,
∴===,
∴△ABC∽△DEF.
