2021-2022学年人教版九年级数学下册 28.2解直角三角形及其应用 期末复习自主提升训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册 28.2解直角三角形及其应用 期末复习自主提升训练(Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 506.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》
期末复习自主提升训练1(附答案)
1.如图,某兴趣小组用无人机对大楼进行测高,无人机从距离大楼30米(PB=30米)垂直起飞,飞到A处悬停,测得大楼底部俯角α=45°,大楼顶部仰角β=60°,则大楼的楼高BC= 米.(结果保留根号)
2.如果一个斜坡的坡度为i=1:2.4,那么这个斜坡坡角α的余弦值等于 .
3.如图,△ABC的顶点都在边长为1的方格的格点上,则sin∠ACB的值为 .
4.如图,在平面直角坐标系中,AB=3,连接AB并延长至C,连接OC,若满足OC2=BC AC,tanα=2,则点C的坐标为 .
5.一段公路路面的坡度为i=1:2.4,如果某人沿着这段公路向上行走了130米,那么此人升高了 米.
6.小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮框内的距离BC=5米,眼镜与底面的距离AB=1.7米,视线AD与水平线的夹角为α,已知,则点D到底面的距离CD是 米.
7.某人沿着坡度i=1:的山坡起点向上走了50米,则他离地面 米高.(坡度:坡面铅直高度与水平宽度的比)
8.如图等腰△ABC,AB=AC,CD平分∠ACB,若S△ACD:S△BCD=3:2,则cos∠ACB= .
9.如图,在边长为10的菱形ABCD中,AC为对角线,∠ABC=60°,M、N分别是边BC,CD上的点,BM=CN,连接MN交AC于P点,当MN最短时,PC长度为 .
10.如图建筑楼顶立有广告牌DE,小亮准备利用所学的数学知识估测该主楼AD的高度.由于场地有限,不便测量,所以小亮沿坡度i=1:0.75的斜坡从看台前的B处步行15米到达C处,此时,测得广告牌底部D的仰角为45°,广告牌顶部E的仰角为60°(身高忽略不计),已知广告牌DE=10米,则该主楼AD的高度约为 米(结果保留根号).
11.某区域平面示意图如图所示,AB和BC是两条互相垂直的公路,AB=800米,甲勘测员在A处测得点D位于北偏东45°,乙勘测员在C处测得点D位于南偏东60°,CD=300米,则公路BC的长为 米.
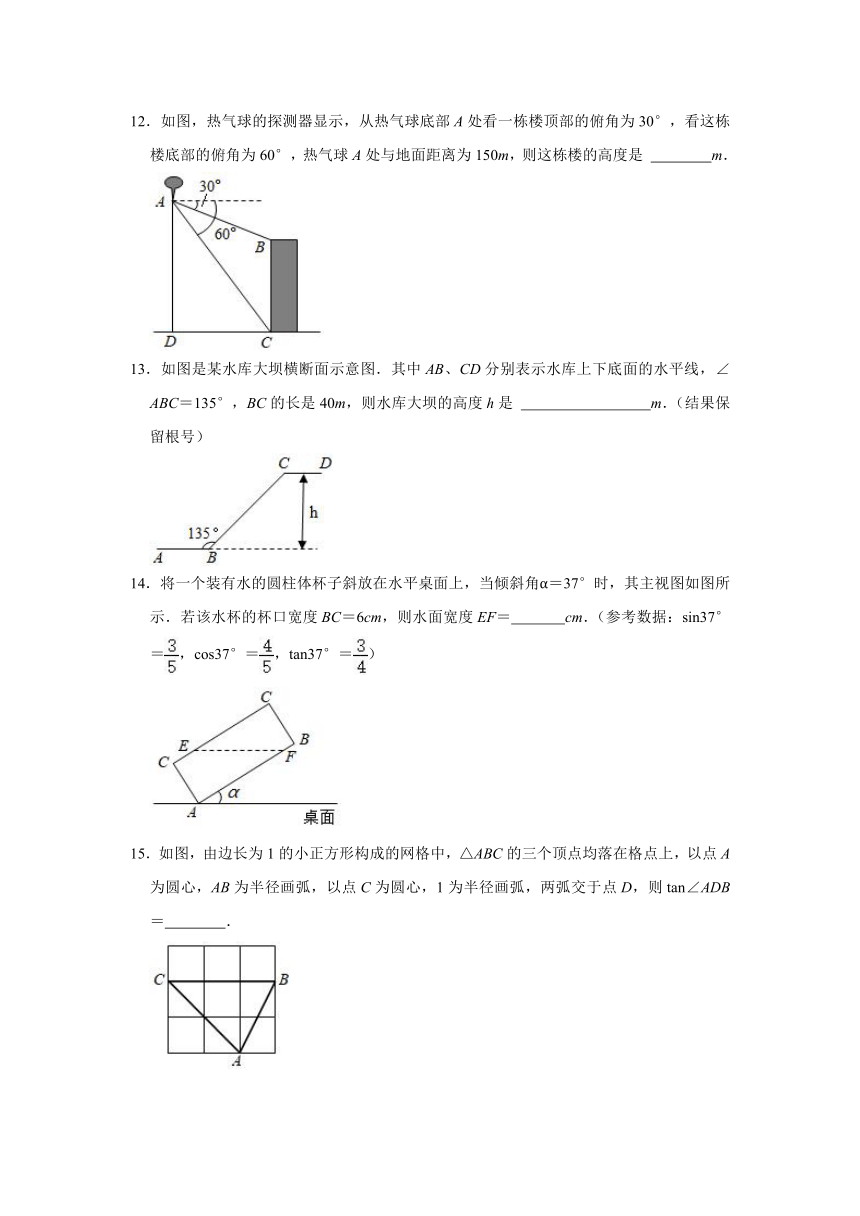
12.如图,热气球的探测器显示,从热气球底部A处看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为150m,则这栋楼的高度是 m.
13.如图是某水库大坝横断面示意图.其中AB、CD分别表示水库上下底面的水平线,∠ABC=135°,BC的长是40m,则水库大坝的高度h是 m.(结果保留根号)
14.将一个装有水的圆柱体杯子斜放在水平桌面上,当倾斜角α=37°时,其主视图如图所示.若该水杯的杯口宽度BC=6cm,则水面宽度EF= cm.(参考数据:sin37°=,cos37°=,tan37°=)
15.如图,由边长为1的小正方形构成的网格中,△ABC的三个顶点均落在格点上,以点A为圆心,AB为半径画弧,以点C为圆心,1为半径画弧,两弧交于点D,则tan∠ADB= .
16.如图,在边长为1的正方形网格中,连接格点A,B和C,D,AB与CD相交于点E,则tan∠AEC= .
17.等腰△ABC中,顶角∠ABC=45°,AM⊥BC,BN⊥AC,AM与BN交于点P,则S△BPM:S△ABP的值为 .
18.为倡导“低碳生活”,人们常常选择共享单车作为代步工具.图1为单车实物图,图2为单车示意图,AB与地面平行,坐垫C可以在射线BE方向自由调节.已知车轮半径为30cm,BE=40cm,∠ABE=75°.小明将坐垫从位置E上移至C,CE=20cm,则此时坐垫C离地面的高度为 cm.(结果精确到1cm)(参考数据:sin75°≈0.966,cos75°≈0.259,tan75°≈3.732).
19.如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向.当在主输气管道AC上寻找支管道连接点N,使到该小区M铺设的管道最短时,AN的长为 米.
20.如图,某同学在附中红星校区(A处)测得他家位置在北偏西45°方向,当他沿红星路向西骑行600米到了市委(B处)的位置,又测得他家在北偏西30°方向,该同学每天从家(C处)出发,先向正南骑行到路口D处,再沿红星路向东到红星校区上学,假设他骑行的速度是250米/分,请你帮他计算一下,他从家到学校大约用 分钟.(结果精确到1分钟,≈1.732)
21.如图,由一段斜坡AB的高AD长为0.6米,∠ABD=30°,为了达到无障碍通道的坡道标准,现准备把斜坡改长,使∠ACD=5.71°.
(1)求斜坡AB的长;
(2)求斜坡新起点C与原起点B的距离.(精确到0.01米)(参考数据:≈1.732,tan5.71°≈0.100)
22.如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
(1)求渔船从B到A的航行过程中与码头M之间的最小距离.
(2)若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.
23.“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
(1)求观测点C到公路MN的距离;
(2)请你判断该汽车是否超速?(参考数据:≈1.41,≈1.73)
24.如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
25.如图,在某建筑物AC上挂着一幅宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°;再往条幅方向前行20m到达点E处,看条幅顶端B,测得仰角为60°,求宣传条幅BC的长.(小明的身高忽略不计,结果保留根号)
26.钓鱼岛自古就是中国的领土,我国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.M、N为钓鱼岛上东西海岸线上的两点,MN之间的距离约为3.6km,某日,我国一艘海监船从A点沿正北方向巡航,在A点测得岛屿的西端点N在点A的北偏东35°方向;海监船继续航行4km后到达B点,测得岛屿的东端点M在点B的北偏东60°方向,求点M距离海监船航线的最短距离(结果精确到0.1km,tan35°≈0.7).
27.博鳌亚洲论坛2018年年会于4月8日在海南博鳌拉开帷幕,组委会在会议中心的墙壁上悬挂会旗,已知矩形DCFE的两边DE,DC长分别为1.6m,1.2m.旗杆DB的长度为2m,DB与墙面AB的夹角∠DBG为35°.当会旗展开时,如图所示,
(1)求DF的长;
(2)求点E到墙壁AB所在直线的距离.(结果精确到0.1m.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
28.如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处测得亭子A在北偏西45°方向上,测得树B在北偏东36°方向上,又测得B、C之间的距离等于200米,求A、B之间的距离
(结果精确到1米).(参考数据:≈1.414,sin36°≈0.588,cos36°≈0.809,tan36°≈0.727,cot36°≈1.376)
29.放风筝是大家喜爱的一种运动星期天的上午小明在金明广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为50°,已知点A,B,C在同一条水平直线上,小明搬了一把梯子来取风筝,梯子能达到的最大高度为20米,请问小明能把风筝捡回来吗?(最后结果精确到1米)(风筝线AD,BD均为线段,≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
30.太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中线段AB、CD、EF表示支撑角钢,太阳能电池板紧贴在支撑角钢AB上且长度均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD、EF与地面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少.(结果保留根号)
参考答案
1.解:过点A作AM⊥BC于M,则∠MAB=45°,∠MAC=60°,BP=AM=30米,
在Rt△ABP中,BP=30米,∠PAB=90°﹣45°=45°,
∴AP=BP=30米=BM,
在Rt△ACM中,∠MAC=60°,AM=30米,
∴CM=AM=30(米),
∴BC=BM+CM=(30+30)米,
故答案为:(30+30).
2.解:如图所示:
由题意,得:tanα=i=1:2.4=,
设斜坡的竖直高度为5x,则水平距离为12x,
则斜坡长==13x,
则cosα==.
故答案为:.
3.解:过点B作BD⊥AC,垂足为D.
由格点可求得:BC==2,
AC==2.
∵S△ABC=×2×2=2,
S△ABC=AC×BD=×2×BD=BD,
∴BD=2,
∴BD=.
∴sinC===.
故答案为:.
4.解:∵∠C=∠C,
∵OC2=BC AC,
即,
∴△OBC∽△OAC,
∴∠A=∠COB,
∵α+∠COB=90°,∠A+∠ABO=90°,
∴∠ABO=α,
∵tanα=2,
∴tan∠ABO=,
∴OA=2OB,
∵AB=3,
由勾股定理可得:OA2+OB2=AB2,
即,
解得:OB=3,
∴OA=6.
∴tanA=.
如图,过点C作CD⊥x轴于点D,
∵tanα=2,
∴设C(﹣m,2m),m>0,
∴AD=6+m,
∵tan∠A=,
∴,
∴,
解得:m=2,
经检验,m=2是原方程的解.
∴点C坐标为:(﹣2,4).
故答案为:(﹣2,4).
5.解:设此人升高了x米,
∵坡比为1:2.4,
∴他行走的水平宽度为2.4x米,
由勾股定理得,x2+(2.4x)2=1302,
解得,x=50,即他沿着垂直方向升高了50米,
故答案为:50.
6.解:如图,过A作AE⊥CD于E,
则四边形ABCE是矩形,
∴AE=BC=5米,CE=AB=1.7米,
在Rt△ADE中,∠DAE=α,tanα==,
∴DE=AE=×5=1.5(米),
∴CD=CE+DE=3.2米.
故答案为:3.2.
7.解:设坡面的竖直高度为x米,则水平距离为x米,
由勾股定理得:x2+(x)2=502,
解得:x=25或x=﹣25(不合题意舍去),
即坡面的竖直高度为25米,
故答案为:25.
8.解:如图,过点A作AE⊥BC于点E,DN⊥AC于N,DM⊥BC于M.
∵CD平分∠ACB,DM⊥BC于M,DN⊥AC于点N,
∴DM=DN.
∵,,
∴S△ACD:S△BCD=AC:BC=3:2.
∵AB=AC,AE⊥BC,
∴BE=CE=.
∴CE:AC=1:3.
∴cos∠ACB=.
故答案为:.
9.解:连接AM、AN,
∵∠ABC=60°,AB=BC=10,
∴△ABC为等边三角形,∠ACB=∠ACD=60°,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(SAS),
∴AM=AN,
∴△AMN为等边三角形,AM=MN,
当MN最短时,AM最短,此时AM⊥BC,如图,
则∠MAC=30°,
∵∠AMP=60°,
∴∠APM=90°,
∵AM=AB=5,
∴AP=AM=,
∴PC=AC﹣AP=10﹣=.
故答案为:.
10.解:过C作CF⊥AE于F,CG⊥AB于G,如图所示:
则四边形AFCG是矩形,
∴AF=CG,
∵斜坡AB的坡度i=1:0.75==,BC=15米,
∴BG=9(米),AF=CG=12(米),
设DF=x米.
在Rt△DCF中,∠DCF=45°,
∴CF=DF=x米.
在Rt△ECF中,∠ECF=60°,
∴EF=tan60° CF=x(米),
∵DE=10米,
∴x﹣x=10,
∴x=5(+1),
∴DF=5(+1)米,
∴AD=AF+DF=12+5(+1)=(17+5)米,
故答案为:(17+5).
11.解:过D作DE⊥OC于E,
∵∠C=60°,CD=300米,
∴CE=CD=150(米),
∴DE=CE=150(米),
∵∠B=90°,AB=800米,∠A=45°,
∴∠AOB=45°,
∴OB=AB=800米,
∵∠DOE=∠AOB=45°,
∴△DEO是等腰直角三角形,
∴OE=DE=150米,
∴公路BC的长为150+150+800=(950+150)(米),
故答案为:(950+150).
12.解:如图,过A作AH⊥BC,交CB的延长线于点H,
在Rt△ACD中,
∵∠CAD=30°,AD=150m,
∴CD=AD tan30°=150×=50(m),
∴AH=CD=50m.
在Rt△ABH中,
∵∠BAH=30°,AH=50m,
∴BH=AH tan30°=50×=50(m),
∴BC=AD﹣BH=150﹣50=100(m),
答:这栋楼的高度为100m.
故答案为:100.
13.解:如图,作CH⊥AB于点H.
∵∠ABC=135°,
∴∠CBH=45°,
∴CH=BC sin45°=40×=20(m),
故答案为:20.
14.解:过E作EH⊥AB于H,
则四边形ACEH是矩形,
∴EH=AC=BC=6cm,∠EHF=∠EHA=90°,
∵EF∥桌面,
∴∠EFA=α=37°,
∴sin37°==,
∴EF=6×=10(cm),
故答案为:10.
15.解:如图1所示:∵AD=AB=,CD=1,
∴点D是符合条件的点.
在Rt△ADM中,tan∠ADB==2.
如图2所示:∵AD=AB=,CD=1,
∴点D是符合条件的点.
∵AD=AB=,BD=,
∴BD2=AD2+AB2.
∴△ADB是直角三角形.
在Rt△ADB中,tan∠ADB==1.
故答案为:2或1.
16.解:连接格点AF、BF.
∵AC∥DF,AC=DF=1,
∴四边形ACDF是平行四边形.
∴AF∥CD.
∴∠FAB=∠CEA.
∵AF=2,BF=,AB=,
∴AB2=AF2+BF2.
∴△AFB是直角三角形.
∴tan∠CEA=tan∠FAB===.
故答案为:.
17.解:如图,过点P作PQ⊥AB于点Q,
∵AB=CB,BN⊥AC,
∴BN平分∠ABC,
∵AM⊥BC,PQ⊥AB,
∴PM=PQ,
∴S△BPM:S△ABP=BM:AB,
∵∠ABC=45°,AM⊥BC,
∴AM=BM,
∴△AMB是等腰直角三角形,
∴sin45°=BM:AB=.
∴S△BPM:S△ABP=.
故答案为:.
18.解:过点C作CN⊥AB,交AB于M,交地面于N.
由题意可知MN=30cm,BC=60cm,
∴在Rt△BCM中,∠ABE=70°,
∴sin∠ABE=sin75°=≈0.966,
∴CM≈58(cm),
∴CN=MN+CM=88(cm),
∴坐垫C离地面的高度为88cm.
故答案为:88.
19.解:如图,过C作东西方向线的平行线交过A的南北方向线AE于B,过M作MN⊥AC交于N点,
则MN最短,
∵∠EAC=60°,∠EAM=30°,
∴∠CAM=30°,
∴∠AMN=60°,
又∵C处看M点为北偏西60°,
∴∠FCM=60°,
∴∠MCB=30°,
∵∠EAC=60°,
∴∠CAD=30°,
∴∠BCA=30°,
∴∠MCA=∠MCB+∠BCA=60°,
∴∠AMC=90°,∠MAC=30°,
∴MC=AC=1000,∠CMN=30°,
∴NC=MC=500,
∵AC=2000米,
∴AN=AC﹣NC=2000﹣500=1500(米),
即该小区M铺设的管道最短时,AN的长为1500米,
故答案为:1500.
20.解:由题意得:∠D=90°,∠BCD=30°,∠A=90°﹣45°=45°,AB=600米,
则AD=BD,△ACD是等腰直角三角形,
∴AD=CD=BD,
∴AD﹣BD=AB,
∴BD﹣BD=600米,
解得:BD=(300+300)米,
∴CD=AD=BD=(900+300)米,
∴CD+AD=(1800+600)米,
∴(1800+600)÷250≈11(分钟),
即某同学从家到学校大约用11分钟,
故答案为:11.
21.解:(1)在Rt△ABD中,AB=AD÷sin30°=0.6÷=1.2(米),
(2)在Rt△ABD中,BD=AD÷tan30°=0.6≈1.039(米),
在Rt△ACD中,CD=AD÷tan5.71°≈6(米),
∴BC=CD﹣BD=6﹣1.039=4.96(米).
答:求斜坡AB的长为1.2米,斜坡新起点C与原起点B的距离为4.96米.
22.解:(1)作MC⊥AB于C,
则MC=BM×cos45°=60海里,
答:渔船从B到A的航行过程中与码头M之间的最小距离为60海里;
(2)在Rt△ACM中,AM==40,
40÷20=2,
答:渔船从A到达码头M的航行时间为2小时.
23.解:(1)过C作CH⊥MN,垂足为H,如图所示:
∵∠CBN=60°,BC=200m,
∴CH=BC sin60°=200×=100(m),
即观测点C到公路MN的距离为100m;
(2)该汽车没有超速.理由如下:
∵BH=BC cos60°=100(米),
∵∠CAN=45°,
∴AH=CH=100m,
∴AB=100﹣100≈73(m),
∴车速为=14.6m/s.
∵60千米/小时=m/s,
又∵14.6<,
∴该汽车没有超速.
24.解:(1)∵DE⊥AB,
∴∠DEA=90°,
∴∠A+∠ADE=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠ADE=∠B,
在Rt△ABC中,∵AC=12,BC=5,
∴AB=13,
∴,
∴;
(2)由(1)得,
设AD为x,则,
∵AC=AD+CD=12,
∴,
解得,
∴.
25.解:∵∠BFC=30°,∠BEC=60°,
∴∠EBF=∠EFB=30°,
∴BE=EF=20m,
在Rt△BEC中,
∵∠BEC=60°,
∴BC=BE sin60°=20×=10m.
答:宣传条幅BC的长为m.
26.解:如图,延长MN交AB于K.设KN=x,KB=y,
在Rt△MBK中,tan60°=,
∴x+3.6=y①
在Rt△ANK中,tan35°=,
∴x=0.7(4+y) ②,
由①②可得x=7.1(km),
∴MK=7.1+3.6=10.7(km),
答:点M距离海监船航线的最短距离为10.7km.
27.解:(1)在Rt△DEF中,由题意知ED=1.6 m,BD=2 m,
DF==2.
答:DF长为2m.
(2)分别做DM⊥AB,EN⊥AB,DH⊥EN,
垂足分别为点M、N、H,
在Rt△DBM中,sin∠DBM=,
∴DM=2 sin35°≈1.14.
∵∠DEC=∠CNB,∠DCE=∠NCB,
∴∠DEC=∠CBN=35°,
在Rt△DEH中,cos∠DEH=,
∴EH=1.6 cos35°≈1.31.
∴EN=EH+HN=1.31+1.14=2.45≈2.5m.
答:E点离墙面AB的最远距离为2.5 m.
28.解:过点C作CH⊥AB,垂足为点H,
由题意,得∠ACH=45°,∠BCH=36°,BC=200,
在Rt△BHC中,,
∴,
∵sin36°≈0.588,
∴BH≈117.6,
又,
∴.
∵cos36°≈0.809,
∴HC≈161.8,
在Rt△AHC中,,
∵∠ACH=45°,
∴AH=HC,
∴AH≈161.8,
又AB=AH+BH,
∴AB≈279.4,
∴AB≈279(米),
答:A、B之间的距离为279米.
29.解:作DH⊥BC于H,设DH=x米.
∵∠ACD=90°,
∴在直角△ADH中,∠DAH=30°,AD=2DH=2x,AH=DH÷tan30°=x,
在直角△BDH中,∠DBH=50°,BH=,BD=DH sin50°=sin50°x,
∵AH﹣BH=AB=10米,
∴x﹣=10,
∴x=,
∴BD==÷0.766≈15(米),
20>15,
∴小明能把风筝捡回来.
30.解:如图所示,延长BA交FD延长线于点G,过点A作AH⊥DG于点H,
由题意知,AB=300cm、BE=AC=50cm、AH=50cm、∠AGH=30°,
在Rt△AGH中,∵AG=2AH=100cm,
∴CG=AC+AG=150cm,
则CD=CG=75cm;
∵EG=AB﹣BE+AG=300﹣50+100=350(cm),
∴在Rt△EFG中,EF=EGtan∠EGF=350tan30°=350×=(cm),
所以支撑角钢CD的长为75cm,EF的长为cm.
期末复习自主提升训练1(附答案)
1.如图,某兴趣小组用无人机对大楼进行测高,无人机从距离大楼30米(PB=30米)垂直起飞,飞到A处悬停,测得大楼底部俯角α=45°,大楼顶部仰角β=60°,则大楼的楼高BC= 米.(结果保留根号)
2.如果一个斜坡的坡度为i=1:2.4,那么这个斜坡坡角α的余弦值等于 .
3.如图,△ABC的顶点都在边长为1的方格的格点上,则sin∠ACB的值为 .
4.如图,在平面直角坐标系中,AB=3,连接AB并延长至C,连接OC,若满足OC2=BC AC,tanα=2,则点C的坐标为 .
5.一段公路路面的坡度为i=1:2.4,如果某人沿着这段公路向上行走了130米,那么此人升高了 米.
6.小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮框内的距离BC=5米,眼镜与底面的距离AB=1.7米,视线AD与水平线的夹角为α,已知,则点D到底面的距离CD是 米.
7.某人沿着坡度i=1:的山坡起点向上走了50米,则他离地面 米高.(坡度:坡面铅直高度与水平宽度的比)
8.如图等腰△ABC,AB=AC,CD平分∠ACB,若S△ACD:S△BCD=3:2,则cos∠ACB= .
9.如图,在边长为10的菱形ABCD中,AC为对角线,∠ABC=60°,M、N分别是边BC,CD上的点,BM=CN,连接MN交AC于P点,当MN最短时,PC长度为 .
10.如图建筑楼顶立有广告牌DE,小亮准备利用所学的数学知识估测该主楼AD的高度.由于场地有限,不便测量,所以小亮沿坡度i=1:0.75的斜坡从看台前的B处步行15米到达C处,此时,测得广告牌底部D的仰角为45°,广告牌顶部E的仰角为60°(身高忽略不计),已知广告牌DE=10米,则该主楼AD的高度约为 米(结果保留根号).
11.某区域平面示意图如图所示,AB和BC是两条互相垂直的公路,AB=800米,甲勘测员在A处测得点D位于北偏东45°,乙勘测员在C处测得点D位于南偏东60°,CD=300米,则公路BC的长为 米.
12.如图,热气球的探测器显示,从热气球底部A处看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为150m,则这栋楼的高度是 m.
13.如图是某水库大坝横断面示意图.其中AB、CD分别表示水库上下底面的水平线,∠ABC=135°,BC的长是40m,则水库大坝的高度h是 m.(结果保留根号)
14.将一个装有水的圆柱体杯子斜放在水平桌面上,当倾斜角α=37°时,其主视图如图所示.若该水杯的杯口宽度BC=6cm,则水面宽度EF= cm.(参考数据:sin37°=,cos37°=,tan37°=)
15.如图,由边长为1的小正方形构成的网格中,△ABC的三个顶点均落在格点上,以点A为圆心,AB为半径画弧,以点C为圆心,1为半径画弧,两弧交于点D,则tan∠ADB= .
16.如图,在边长为1的正方形网格中,连接格点A,B和C,D,AB与CD相交于点E,则tan∠AEC= .
17.等腰△ABC中,顶角∠ABC=45°,AM⊥BC,BN⊥AC,AM与BN交于点P,则S△BPM:S△ABP的值为 .
18.为倡导“低碳生活”,人们常常选择共享单车作为代步工具.图1为单车实物图,图2为单车示意图,AB与地面平行,坐垫C可以在射线BE方向自由调节.已知车轮半径为30cm,BE=40cm,∠ABE=75°.小明将坐垫从位置E上移至C,CE=20cm,则此时坐垫C离地面的高度为 cm.(结果精确到1cm)(参考数据:sin75°≈0.966,cos75°≈0.259,tan75°≈3.732).
19.如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向.当在主输气管道AC上寻找支管道连接点N,使到该小区M铺设的管道最短时,AN的长为 米.
20.如图,某同学在附中红星校区(A处)测得他家位置在北偏西45°方向,当他沿红星路向西骑行600米到了市委(B处)的位置,又测得他家在北偏西30°方向,该同学每天从家(C处)出发,先向正南骑行到路口D处,再沿红星路向东到红星校区上学,假设他骑行的速度是250米/分,请你帮他计算一下,他从家到学校大约用 分钟.(结果精确到1分钟,≈1.732)
21.如图,由一段斜坡AB的高AD长为0.6米,∠ABD=30°,为了达到无障碍通道的坡道标准,现准备把斜坡改长,使∠ACD=5.71°.
(1)求斜坡AB的长;
(2)求斜坡新起点C与原起点B的距离.(精确到0.01米)(参考数据:≈1.732,tan5.71°≈0.100)
22.如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
(1)求渔船从B到A的航行过程中与码头M之间的最小距离.
(2)若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.
23.“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
(1)求观测点C到公路MN的距离;
(2)请你判断该汽车是否超速?(参考数据:≈1.41,≈1.73)
24.如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
25.如图,在某建筑物AC上挂着一幅宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°;再往条幅方向前行20m到达点E处,看条幅顶端B,测得仰角为60°,求宣传条幅BC的长.(小明的身高忽略不计,结果保留根号)
26.钓鱼岛自古就是中国的领土,我国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.M、N为钓鱼岛上东西海岸线上的两点,MN之间的距离约为3.6km,某日,我国一艘海监船从A点沿正北方向巡航,在A点测得岛屿的西端点N在点A的北偏东35°方向;海监船继续航行4km后到达B点,测得岛屿的东端点M在点B的北偏东60°方向,求点M距离海监船航线的最短距离(结果精确到0.1km,tan35°≈0.7).
27.博鳌亚洲论坛2018年年会于4月8日在海南博鳌拉开帷幕,组委会在会议中心的墙壁上悬挂会旗,已知矩形DCFE的两边DE,DC长分别为1.6m,1.2m.旗杆DB的长度为2m,DB与墙面AB的夹角∠DBG为35°.当会旗展开时,如图所示,
(1)求DF的长;
(2)求点E到墙壁AB所在直线的距离.(结果精确到0.1m.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
28.如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处测得亭子A在北偏西45°方向上,测得树B在北偏东36°方向上,又测得B、C之间的距离等于200米,求A、B之间的距离
(结果精确到1米).(参考数据:≈1.414,sin36°≈0.588,cos36°≈0.809,tan36°≈0.727,cot36°≈1.376)
29.放风筝是大家喜爱的一种运动星期天的上午小明在金明广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为50°,已知点A,B,C在同一条水平直线上,小明搬了一把梯子来取风筝,梯子能达到的最大高度为20米,请问小明能把风筝捡回来吗?(最后结果精确到1米)(风筝线AD,BD均为线段,≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
30.太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中线段AB、CD、EF表示支撑角钢,太阳能电池板紧贴在支撑角钢AB上且长度均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD、EF与地面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少.(结果保留根号)
参考答案
1.解:过点A作AM⊥BC于M,则∠MAB=45°,∠MAC=60°,BP=AM=30米,
在Rt△ABP中,BP=30米,∠PAB=90°﹣45°=45°,
∴AP=BP=30米=BM,
在Rt△ACM中,∠MAC=60°,AM=30米,
∴CM=AM=30(米),
∴BC=BM+CM=(30+30)米,
故答案为:(30+30).
2.解:如图所示:
由题意,得:tanα=i=1:2.4=,
设斜坡的竖直高度为5x,则水平距离为12x,
则斜坡长==13x,
则cosα==.
故答案为:.
3.解:过点B作BD⊥AC,垂足为D.
由格点可求得:BC==2,
AC==2.
∵S△ABC=×2×2=2,
S△ABC=AC×BD=×2×BD=BD,
∴BD=2,
∴BD=.
∴sinC===.
故答案为:.
4.解:∵∠C=∠C,
∵OC2=BC AC,
即,
∴△OBC∽△OAC,
∴∠A=∠COB,
∵α+∠COB=90°,∠A+∠ABO=90°,
∴∠ABO=α,
∵tanα=2,
∴tan∠ABO=,
∴OA=2OB,
∵AB=3,
由勾股定理可得:OA2+OB2=AB2,
即,
解得:OB=3,
∴OA=6.
∴tanA=.
如图,过点C作CD⊥x轴于点D,
∵tanα=2,
∴设C(﹣m,2m),m>0,
∴AD=6+m,
∵tan∠A=,
∴,
∴,
解得:m=2,
经检验,m=2是原方程的解.
∴点C坐标为:(﹣2,4).
故答案为:(﹣2,4).
5.解:设此人升高了x米,
∵坡比为1:2.4,
∴他行走的水平宽度为2.4x米,
由勾股定理得,x2+(2.4x)2=1302,
解得,x=50,即他沿着垂直方向升高了50米,
故答案为:50.
6.解:如图,过A作AE⊥CD于E,
则四边形ABCE是矩形,
∴AE=BC=5米,CE=AB=1.7米,
在Rt△ADE中,∠DAE=α,tanα==,
∴DE=AE=×5=1.5(米),
∴CD=CE+DE=3.2米.
故答案为:3.2.
7.解:设坡面的竖直高度为x米,则水平距离为x米,
由勾股定理得:x2+(x)2=502,
解得:x=25或x=﹣25(不合题意舍去),
即坡面的竖直高度为25米,
故答案为:25.
8.解:如图,过点A作AE⊥BC于点E,DN⊥AC于N,DM⊥BC于M.
∵CD平分∠ACB,DM⊥BC于M,DN⊥AC于点N,
∴DM=DN.
∵,,
∴S△ACD:S△BCD=AC:BC=3:2.
∵AB=AC,AE⊥BC,
∴BE=CE=.
∴CE:AC=1:3.
∴cos∠ACB=.
故答案为:.
9.解:连接AM、AN,
∵∠ABC=60°,AB=BC=10,
∴△ABC为等边三角形,∠ACB=∠ACD=60°,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(SAS),
∴AM=AN,
∴△AMN为等边三角形,AM=MN,
当MN最短时,AM最短,此时AM⊥BC,如图,
则∠MAC=30°,
∵∠AMP=60°,
∴∠APM=90°,
∵AM=AB=5,
∴AP=AM=,
∴PC=AC﹣AP=10﹣=.
故答案为:.
10.解:过C作CF⊥AE于F,CG⊥AB于G,如图所示:
则四边形AFCG是矩形,
∴AF=CG,
∵斜坡AB的坡度i=1:0.75==,BC=15米,
∴BG=9(米),AF=CG=12(米),
设DF=x米.
在Rt△DCF中,∠DCF=45°,
∴CF=DF=x米.
在Rt△ECF中,∠ECF=60°,
∴EF=tan60° CF=x(米),
∵DE=10米,
∴x﹣x=10,
∴x=5(+1),
∴DF=5(+1)米,
∴AD=AF+DF=12+5(+1)=(17+5)米,
故答案为:(17+5).
11.解:过D作DE⊥OC于E,
∵∠C=60°,CD=300米,
∴CE=CD=150(米),
∴DE=CE=150(米),
∵∠B=90°,AB=800米,∠A=45°,
∴∠AOB=45°,
∴OB=AB=800米,
∵∠DOE=∠AOB=45°,
∴△DEO是等腰直角三角形,
∴OE=DE=150米,
∴公路BC的长为150+150+800=(950+150)(米),
故答案为:(950+150).
12.解:如图,过A作AH⊥BC,交CB的延长线于点H,
在Rt△ACD中,
∵∠CAD=30°,AD=150m,
∴CD=AD tan30°=150×=50(m),
∴AH=CD=50m.
在Rt△ABH中,
∵∠BAH=30°,AH=50m,
∴BH=AH tan30°=50×=50(m),
∴BC=AD﹣BH=150﹣50=100(m),
答:这栋楼的高度为100m.
故答案为:100.
13.解:如图,作CH⊥AB于点H.
∵∠ABC=135°,
∴∠CBH=45°,
∴CH=BC sin45°=40×=20(m),
故答案为:20.
14.解:过E作EH⊥AB于H,
则四边形ACEH是矩形,
∴EH=AC=BC=6cm,∠EHF=∠EHA=90°,
∵EF∥桌面,
∴∠EFA=α=37°,
∴sin37°==,
∴EF=6×=10(cm),
故答案为:10.
15.解:如图1所示:∵AD=AB=,CD=1,
∴点D是符合条件的点.
在Rt△ADM中,tan∠ADB==2.
如图2所示:∵AD=AB=,CD=1,
∴点D是符合条件的点.
∵AD=AB=,BD=,
∴BD2=AD2+AB2.
∴△ADB是直角三角形.
在Rt△ADB中,tan∠ADB==1.
故答案为:2或1.
16.解:连接格点AF、BF.
∵AC∥DF,AC=DF=1,
∴四边形ACDF是平行四边形.
∴AF∥CD.
∴∠FAB=∠CEA.
∵AF=2,BF=,AB=,
∴AB2=AF2+BF2.
∴△AFB是直角三角形.
∴tan∠CEA=tan∠FAB===.
故答案为:.
17.解:如图,过点P作PQ⊥AB于点Q,
∵AB=CB,BN⊥AC,
∴BN平分∠ABC,
∵AM⊥BC,PQ⊥AB,
∴PM=PQ,
∴S△BPM:S△ABP=BM:AB,
∵∠ABC=45°,AM⊥BC,
∴AM=BM,
∴△AMB是等腰直角三角形,
∴sin45°=BM:AB=.
∴S△BPM:S△ABP=.
故答案为:.
18.解:过点C作CN⊥AB,交AB于M,交地面于N.
由题意可知MN=30cm,BC=60cm,
∴在Rt△BCM中,∠ABE=70°,
∴sin∠ABE=sin75°=≈0.966,
∴CM≈58(cm),
∴CN=MN+CM=88(cm),
∴坐垫C离地面的高度为88cm.
故答案为:88.
19.解:如图,过C作东西方向线的平行线交过A的南北方向线AE于B,过M作MN⊥AC交于N点,
则MN最短,
∵∠EAC=60°,∠EAM=30°,
∴∠CAM=30°,
∴∠AMN=60°,
又∵C处看M点为北偏西60°,
∴∠FCM=60°,
∴∠MCB=30°,
∵∠EAC=60°,
∴∠CAD=30°,
∴∠BCA=30°,
∴∠MCA=∠MCB+∠BCA=60°,
∴∠AMC=90°,∠MAC=30°,
∴MC=AC=1000,∠CMN=30°,
∴NC=MC=500,
∵AC=2000米,
∴AN=AC﹣NC=2000﹣500=1500(米),
即该小区M铺设的管道最短时,AN的长为1500米,
故答案为:1500.
20.解:由题意得:∠D=90°,∠BCD=30°,∠A=90°﹣45°=45°,AB=600米,
则AD=BD,△ACD是等腰直角三角形,
∴AD=CD=BD,
∴AD﹣BD=AB,
∴BD﹣BD=600米,
解得:BD=(300+300)米,
∴CD=AD=BD=(900+300)米,
∴CD+AD=(1800+600)米,
∴(1800+600)÷250≈11(分钟),
即某同学从家到学校大约用11分钟,
故答案为:11.
21.解:(1)在Rt△ABD中,AB=AD÷sin30°=0.6÷=1.2(米),
(2)在Rt△ABD中,BD=AD÷tan30°=0.6≈1.039(米),
在Rt△ACD中,CD=AD÷tan5.71°≈6(米),
∴BC=CD﹣BD=6﹣1.039=4.96(米).
答:求斜坡AB的长为1.2米,斜坡新起点C与原起点B的距离为4.96米.
22.解:(1)作MC⊥AB于C,
则MC=BM×cos45°=60海里,
答:渔船从B到A的航行过程中与码头M之间的最小距离为60海里;
(2)在Rt△ACM中,AM==40,
40÷20=2,
答:渔船从A到达码头M的航行时间为2小时.
23.解:(1)过C作CH⊥MN,垂足为H,如图所示:
∵∠CBN=60°,BC=200m,
∴CH=BC sin60°=200×=100(m),
即观测点C到公路MN的距离为100m;
(2)该汽车没有超速.理由如下:
∵BH=BC cos60°=100(米),
∵∠CAN=45°,
∴AH=CH=100m,
∴AB=100﹣100≈73(m),
∴车速为=14.6m/s.
∵60千米/小时=m/s,
又∵14.6<,
∴该汽车没有超速.
24.解:(1)∵DE⊥AB,
∴∠DEA=90°,
∴∠A+∠ADE=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠ADE=∠B,
在Rt△ABC中,∵AC=12,BC=5,
∴AB=13,
∴,
∴;
(2)由(1)得,
设AD为x,则,
∵AC=AD+CD=12,
∴,
解得,
∴.
25.解:∵∠BFC=30°,∠BEC=60°,
∴∠EBF=∠EFB=30°,
∴BE=EF=20m,
在Rt△BEC中,
∵∠BEC=60°,
∴BC=BE sin60°=20×=10m.
答:宣传条幅BC的长为m.
26.解:如图,延长MN交AB于K.设KN=x,KB=y,
在Rt△MBK中,tan60°=,
∴x+3.6=y①
在Rt△ANK中,tan35°=,
∴x=0.7(4+y) ②,
由①②可得x=7.1(km),
∴MK=7.1+3.6=10.7(km),
答:点M距离海监船航线的最短距离为10.7km.
27.解:(1)在Rt△DEF中,由题意知ED=1.6 m,BD=2 m,
DF==2.
答:DF长为2m.
(2)分别做DM⊥AB,EN⊥AB,DH⊥EN,
垂足分别为点M、N、H,
在Rt△DBM中,sin∠DBM=,
∴DM=2 sin35°≈1.14.
∵∠DEC=∠CNB,∠DCE=∠NCB,
∴∠DEC=∠CBN=35°,
在Rt△DEH中,cos∠DEH=,
∴EH=1.6 cos35°≈1.31.
∴EN=EH+HN=1.31+1.14=2.45≈2.5m.
答:E点离墙面AB的最远距离为2.5 m.
28.解:过点C作CH⊥AB,垂足为点H,
由题意,得∠ACH=45°,∠BCH=36°,BC=200,
在Rt△BHC中,,
∴,
∵sin36°≈0.588,
∴BH≈117.6,
又,
∴.
∵cos36°≈0.809,
∴HC≈161.8,
在Rt△AHC中,,
∵∠ACH=45°,
∴AH=HC,
∴AH≈161.8,
又AB=AH+BH,
∴AB≈279.4,
∴AB≈279(米),
答:A、B之间的距离为279米.
29.解:作DH⊥BC于H,设DH=x米.
∵∠ACD=90°,
∴在直角△ADH中,∠DAH=30°,AD=2DH=2x,AH=DH÷tan30°=x,
在直角△BDH中,∠DBH=50°,BH=,BD=DH sin50°=sin50°x,
∵AH﹣BH=AB=10米,
∴x﹣=10,
∴x=,
∴BD==÷0.766≈15(米),
20>15,
∴小明能把风筝捡回来.
30.解:如图所示,延长BA交FD延长线于点G,过点A作AH⊥DG于点H,
由题意知,AB=300cm、BE=AC=50cm、AH=50cm、∠AGH=30°,
在Rt△AGH中,∵AG=2AH=100cm,
∴CG=AC+AG=150cm,
则CD=CG=75cm;
∵EG=AB﹣BE+AG=300﹣50+100=350(cm),
∴在Rt△EFG中,EF=EGtan∠EGF=350tan30°=350×=(cm),
所以支撑角钢CD的长为75cm,EF的长为cm.
