2021-2022学年北师大版九年级数学上册4.4探索三角形相似的条件 寒假自主复习提升训练 (word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.4探索三角形相似的条件 寒假自主复习提升训练 (word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 249.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 15:55:52 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学上册《探索三角形相似的条件》
寒假自主复习提升训练(附答案)
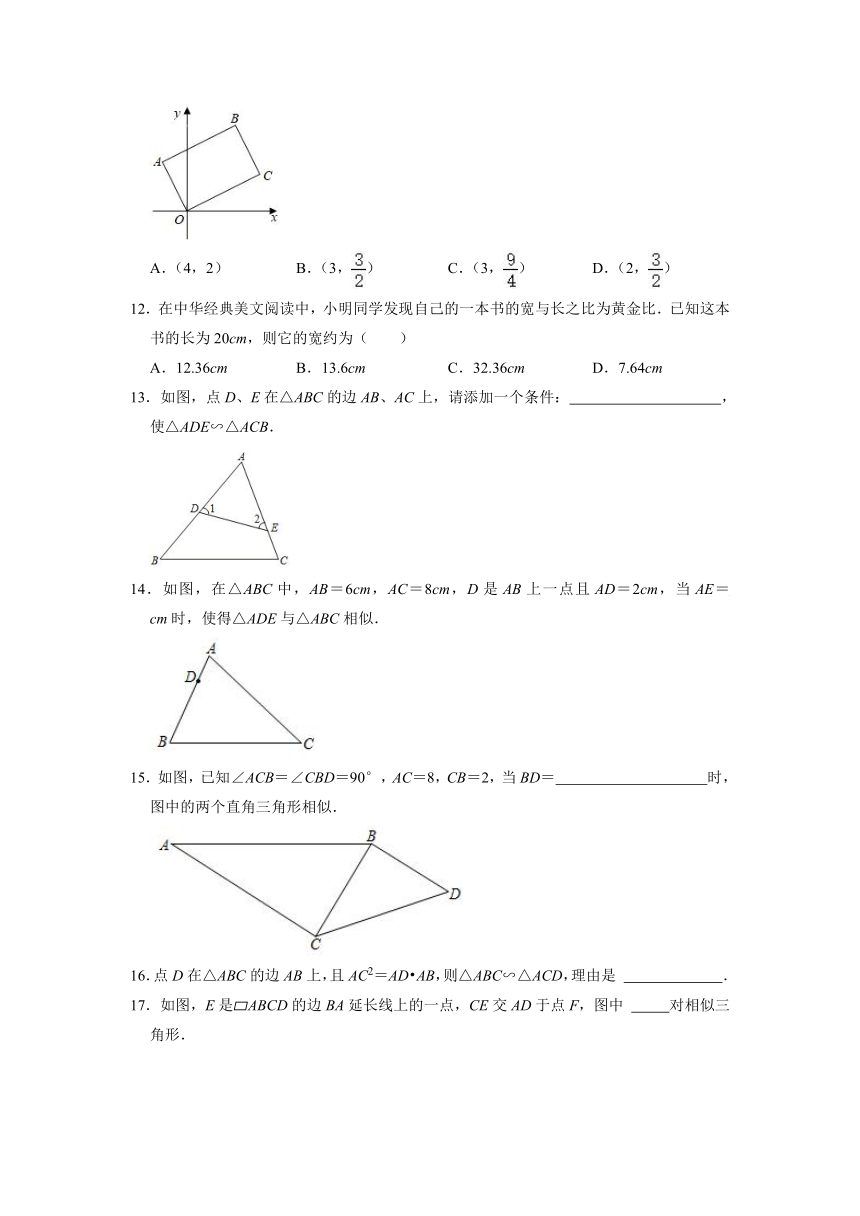
1.如图,△ACD∽△ABC需具备的条件是( )
A.= B.= C.= D.=
2.如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A.B. C.D.
3.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A.B.C.D.
4.如图,点E在 ABCD的边BC延长线上,连AE,交边CD于点F.在不添加辅助线的情况下,图中相似三角形有( )
A.1对 B.2对 C.3对 D.4对
5.点P是△ABC中AB边上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似,满足这样条件的直线最多有( )
A.2条 B.3条 C.4条 D.5条
6.平面直角坐标系中,直线y=﹣x+2和x、y轴交于B、A两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为( )
A.2 B.3 C.4 D.5
7.如图,在正方形网格上,与△ABC相似的三角形是( )
A.△AFD B.△FED C.△AED D.不能确定
8.如图,在Rt△ABC中,CD是斜边AB上的高,则图中的相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
9.如图所示,在△ABC中,AB=6,AC=4,P是AC的中点,过P点的直线交AB于点Q,若以A、P、Q为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ的长为( )
A.3 B.3或 C.3或 D.
10.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
11.将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是,则点C的坐标是( )
A.(4,2) B.(3,) C.(3,) D.(2,)
12.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm,则它的宽约为( )
A.12.36cm B.13.6cm C.32.36cm D.7.64cm
13.如图,点D、E在△ABC的边AB、AC上,请添加一个条件: ,使△ADE∽△ACB.
14.如图,在△ABC中,AB=6cm,AC=8cm,D是AB上一点且AD=2cm,当AE= cm时,使得△ADE与△ABC相似.
15.如图,已知∠ACB=∠CBD=90°,AC=8,CB=2,当BD= 时,图中的两个直角三角形相似.
16.点D在△ABC的边AB上,且AC2=AD AB,则△ABC∽△ACD,理由是 .
17.如图,E是 ABCD的边BA延长线上的一点,CE交AD于点F,图中 对相似三角形.
18.如图,在矩形ABCD中,AB=2,BC=1,点E是DC上一点,∠DAE=∠BAC,则EC的长为 .
19.如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD AB,其中单独能够判定△ABC∽△ACD的有 .
20.定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线.在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC= 度.
21.如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
22.如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.
(1)求证:△ABE∽△ECF;
(2)连接AF,试探究当点E在BC什么位置时,∠BAE=∠EAF,请证明你的结论.
23.如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
24.如图,已知△ABC,AB=AC,∠A=36°.
(1)作∠B的平分线与AC交于点D.(尺规作图,保留作图痕迹,不写作法)
(2)求证:△BDC∽△ABC.
参考答案
1.解:在△ACD和△ABC中,∠A=∠A,
∴根据有两边对应成比例,且夹角相等的两三角形相似,得出添加的条件是:=,
∴=.
故选:C.
2.解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确;
D、两三角形对应边成比例(4﹣1):6=(6﹣4):4且夹角相等,故两三角形相似,故本选项错误.
故选:C.
3.解:根据勾股定理,AC==2,BC=,
所以,夹直角的两边的比为=2,
观各选项,只有C选项三角形符合,与所给图形的三角形相似.
故选:C.
4.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴△AFD∽△EFC∽△EAB.
故选:C.
5.解:(1)作∠APD=∠C
∵∠A=∠A
∴△APD∽△ABC
(2)作PE∥BC
∴△APE∽△ABC
(3)作∠BPF=∠C
∵∠B=∠B
∴△FBP∽△ABC
(4)作PG∥AC
∴△PBG∽△ABC
所以共4条
故选:C.
6.解:如图,
①分别过点O、点A作AB、OB的平行线交于点P1,则△OAP1与△AOB相似(全等),
②作AP2⊥OP1,垂足为P2则△AOP2与△AOB相似.
③作∠AOP3=∠ABO交AP1于P3,则△AOP3与△AOB相似.
④作AP4⊥OP3垂足为P4,则△AOP4与△AOB相似.
故选:C.
7.解:∵AF=4,DF=4,AD=4,AB=2,BC=2,AC=2,
∴=2,
∴△AFD∽△ABC,
故选:A.
8.解:∵∠ACB=90°,CD⊥AB
∴△ABC∽△ACD
△ACD∽△CBD
△ABC∽△CBD
所以有三对相似三角形,
故选:C.
9.解:当△ABC∽△AQP时,,即,AQ=3;
当△ABC∽△APQ时,,即,AQ=,
故选:B.
10.解:△ABC中,∠ABC=90°,AB=6,BC=3,AB:BC=2.
A、当点E的坐标为(6,0)时,∠CDE=90°,CD=2,DE=1,则AB:BC=CD:DE,△CDE∽△ABC,故本选项不符合题意;
B、当点E的坐标为(6,3)时,∠CDE=90°,CD=2,DE=2,则AB:BC≠CD:DE,△CDE与△ABC不相似,故本选项符合题意;
C、当点E的坐标为(6,5)时,∠CDE=90°,CD=2,DE=4,则AB:BC=DE:CD,△EDC∽△ABC,故本选项不符合题意;
D、当点E的坐标为(4,2)时,∠ECD=90°,CD=2,CE=1,则AB:BC=CD:CE,△DCE∽△ABC,故本选项不符合题意;
故选:B.
11.解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,过点A作AN⊥BF于点N,
过点C作CM⊥x轴于点M,
∵∠EAO+∠AOE=90°,∠AOE+∠MOC=90°,
∴∠EAO=∠COM,
又∵∠AEO=∠CMO=90°,
∴△AEO∽△OMC,
∴,
∵∠BAN+∠OAN=90°,∠EAO+∠OAN=90°,
∴∠BAN=∠EAO=∠COM,
在△ABN和△OCM中,
,
∴△ABN≌△OCM(AAS),
∴BN=CM,
∵点A(﹣1,2),点B的纵坐标是,
∴BN=,
∴CM=,
∴,
∴MO=3,
∴点C的坐标是:(3,).
故选:B.
12.解:方法1:设书的宽为x,则有(20+x):20=20:x,解得x=12.36cm.
方法2:书的宽为20×0.618=12.36cm.
故选:A.
13.解:∵∠DAE=∠CAB
∴当∠1=∠C或∠2=∠B或=时,△ADE∽△ACB.
故答案是:∠1=∠C或∠2=∠B或=,
14.解:有两种情形:
如图,当∠ADE=∠B时,△ADE∽△ABC,
∴,
∴,
∴AE=(cm),
当∠ADE′=∠C时,∵∠A=∠A,
∴△ADE′∽△ACB,
∴=,
∴,
∴AE′=1.5(cm),
故答案为:或1.5.
15.解:∵∠ACB=∠CBD=90°,
∴要使△ACB和△CBD相似,
必须或,
将AC=8,CB=2代入上式,得=或,
∴BD=或8.
∴当BD=或8时,图中的两个直角三角形相似.
故答案为:或8.
16.证明:∵AC2=AD AB,
∴AC:AB=AD:AC.
又∵∠A=∠A,
∴△ACD∽△ABC.
故理由是两边对应成比例及夹角相等,两三角形相似.
故答案为:两边对应成比例及夹角相等,两三角形相似.
17.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△AEF∽△DCF,△AEF∽△BEC,
∴△BEC∽△DCF,
故图中三对相似三角形.
故答案为:三.
18.解:矩形ABCD中,DC=AB=2,AD=BC=1,
又∵∠DAE=∠BAC,∠D=∠B,
∴△ADE∽△ABC,
∴AB:AD=BC:DE,
∴=,
∴DE=,
∴EC=DC﹣DE=.
故答案为:.
19.解:由图可知∠A为两个要证明相似的三角形的公共角,
因此,只要再找出一组对应角相等,或两组对应边成比例即可证明△ABC∽△ACD.
而①②④分别与∠A为△ABC与△ACD的公共角相结合,均可推出△ABC∽△ACD.
③中∠A不是已知的比例线段的夹角,故不正确.
∴选①②④.
故答案为:①②④.
20.解:如图所示,∵∠ABC=70°,BD平分∠ABC,
∴∠ABD=∠DBC,
又∵对角线BD是它的相似对角线,
∴△ABD∽△DBC,
∴∠A=∠BDC,∠ADB=∠C,
∴∠A+∠C=∠ADC,
又∵∠A+∠C+∠ADC=360°﹣70°=290°,
∴∠ADC=145°,
故答案为:145.
21.解:设经过t秒时,以△QBP与△ABC相似,则AP=2t厘米,BP=(8﹣2t)厘米,BQ=4t厘米,
∵∠PBQ=∠ABC,
∴当=时,△BPQ∽△BAC,即=,解得t=2(s);
当=时,△BPQ∽△BCA,即=,解得t=0.8(s);
即经过2秒或0.8秒时,△QBP与△ABC相似.
22.(1)证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF;
(2)E是中点时,∠BAE=∠EAF,
理由如下:
连接AF,延长AE于DC的延长线相交于点H,
∵E为BC中点,
∴BE=CE,
∵AB∥DH,
∴∠B=∠ECH,
∵∠AEB=∠CEH,
∴△ABE≌△HCE,
∴AE=EH,
∵EF⊥AH,
∴△AFH是等腰三角形,
∴∠EAF=∠H,
∵AB∥DH,
∴∠H=∠BAE,
∴∠BAE=∠EAF,
∴当点E在BC中点位置时,∠BAE=∠EAF.
23.解:(1)△ABE与△ADF相似.理由如下:
∵四边形ABCD为矩形,DF⊥AE,
∴∠ABE=∠AFD=90°,
∠AEB=∠DAF,
∴△ABE∽△DFA.
(2)∵△ABE∽△ADF
∴=,
∵在Rt△ABE中,AB=6,BE=8,
∴AE=10
∴DF===7.2.
答:DF的长为7.2.
24.(1)解:如图,射线BD即为所求;
(2)证明:在△ABC中,
∵∠A+∠ABC+∠ACB=180°,AB=AC,∠A=36°,
∴∠ABC=∠ACB=(180°﹣∠A)=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=ABC=×72°=36°,
∴∠CBD=∠CAB,
∵∠BCD=∠ACB,
∴△BDC∽△ABC.
寒假自主复习提升训练(附答案)
1.如图,△ACD∽△ABC需具备的条件是( )
A.= B.= C.= D.=
2.如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A.B. C.D.
3.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A.B.C.D.
4.如图,点E在 ABCD的边BC延长线上,连AE,交边CD于点F.在不添加辅助线的情况下,图中相似三角形有( )
A.1对 B.2对 C.3对 D.4对
5.点P是△ABC中AB边上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似,满足这样条件的直线最多有( )
A.2条 B.3条 C.4条 D.5条
6.平面直角坐标系中,直线y=﹣x+2和x、y轴交于B、A两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为( )
A.2 B.3 C.4 D.5
7.如图,在正方形网格上,与△ABC相似的三角形是( )
A.△AFD B.△FED C.△AED D.不能确定
8.如图,在Rt△ABC中,CD是斜边AB上的高,则图中的相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
9.如图所示,在△ABC中,AB=6,AC=4,P是AC的中点,过P点的直线交AB于点Q,若以A、P、Q为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ的长为( )
A.3 B.3或 C.3或 D.
10.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
11.将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是,则点C的坐标是( )
A.(4,2) B.(3,) C.(3,) D.(2,)
12.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm,则它的宽约为( )
A.12.36cm B.13.6cm C.32.36cm D.7.64cm
13.如图,点D、E在△ABC的边AB、AC上,请添加一个条件: ,使△ADE∽△ACB.
14.如图,在△ABC中,AB=6cm,AC=8cm,D是AB上一点且AD=2cm,当AE= cm时,使得△ADE与△ABC相似.
15.如图,已知∠ACB=∠CBD=90°,AC=8,CB=2,当BD= 时,图中的两个直角三角形相似.
16.点D在△ABC的边AB上,且AC2=AD AB,则△ABC∽△ACD,理由是 .
17.如图,E是 ABCD的边BA延长线上的一点,CE交AD于点F,图中 对相似三角形.
18.如图,在矩形ABCD中,AB=2,BC=1,点E是DC上一点,∠DAE=∠BAC,则EC的长为 .
19.如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD AB,其中单独能够判定△ABC∽△ACD的有 .
20.定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线.在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC= 度.
21.如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
22.如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.
(1)求证:△ABE∽△ECF;
(2)连接AF,试探究当点E在BC什么位置时,∠BAE=∠EAF,请证明你的结论.
23.如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
24.如图,已知△ABC,AB=AC,∠A=36°.
(1)作∠B的平分线与AC交于点D.(尺规作图,保留作图痕迹,不写作法)
(2)求证:△BDC∽△ABC.
参考答案
1.解:在△ACD和△ABC中,∠A=∠A,
∴根据有两边对应成比例,且夹角相等的两三角形相似,得出添加的条件是:=,
∴=.
故选:C.
2.解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确;
D、两三角形对应边成比例(4﹣1):6=(6﹣4):4且夹角相等,故两三角形相似,故本选项错误.
故选:C.
3.解:根据勾股定理,AC==2,BC=,
所以,夹直角的两边的比为=2,
观各选项,只有C选项三角形符合,与所给图形的三角形相似.
故选:C.
4.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴△AFD∽△EFC∽△EAB.
故选:C.
5.解:(1)作∠APD=∠C
∵∠A=∠A
∴△APD∽△ABC
(2)作PE∥BC
∴△APE∽△ABC
(3)作∠BPF=∠C
∵∠B=∠B
∴△FBP∽△ABC
(4)作PG∥AC
∴△PBG∽△ABC
所以共4条
故选:C.
6.解:如图,
①分别过点O、点A作AB、OB的平行线交于点P1,则△OAP1与△AOB相似(全等),
②作AP2⊥OP1,垂足为P2则△AOP2与△AOB相似.
③作∠AOP3=∠ABO交AP1于P3,则△AOP3与△AOB相似.
④作AP4⊥OP3垂足为P4,则△AOP4与△AOB相似.
故选:C.
7.解:∵AF=4,DF=4,AD=4,AB=2,BC=2,AC=2,
∴=2,
∴△AFD∽△ABC,
故选:A.
8.解:∵∠ACB=90°,CD⊥AB
∴△ABC∽△ACD
△ACD∽△CBD
△ABC∽△CBD
所以有三对相似三角形,
故选:C.
9.解:当△ABC∽△AQP时,,即,AQ=3;
当△ABC∽△APQ时,,即,AQ=,
故选:B.
10.解:△ABC中,∠ABC=90°,AB=6,BC=3,AB:BC=2.
A、当点E的坐标为(6,0)时,∠CDE=90°,CD=2,DE=1,则AB:BC=CD:DE,△CDE∽△ABC,故本选项不符合题意;
B、当点E的坐标为(6,3)时,∠CDE=90°,CD=2,DE=2,则AB:BC≠CD:DE,△CDE与△ABC不相似,故本选项符合题意;
C、当点E的坐标为(6,5)时,∠CDE=90°,CD=2,DE=4,则AB:BC=DE:CD,△EDC∽△ABC,故本选项不符合题意;
D、当点E的坐标为(4,2)时,∠ECD=90°,CD=2,CE=1,则AB:BC=CD:CE,△DCE∽△ABC,故本选项不符合题意;
故选:B.
11.解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,过点A作AN⊥BF于点N,
过点C作CM⊥x轴于点M,
∵∠EAO+∠AOE=90°,∠AOE+∠MOC=90°,
∴∠EAO=∠COM,
又∵∠AEO=∠CMO=90°,
∴△AEO∽△OMC,
∴,
∵∠BAN+∠OAN=90°,∠EAO+∠OAN=90°,
∴∠BAN=∠EAO=∠COM,
在△ABN和△OCM中,
,
∴△ABN≌△OCM(AAS),
∴BN=CM,
∵点A(﹣1,2),点B的纵坐标是,
∴BN=,
∴CM=,
∴,
∴MO=3,
∴点C的坐标是:(3,).
故选:B.
12.解:方法1:设书的宽为x,则有(20+x):20=20:x,解得x=12.36cm.
方法2:书的宽为20×0.618=12.36cm.
故选:A.
13.解:∵∠DAE=∠CAB
∴当∠1=∠C或∠2=∠B或=时,△ADE∽△ACB.
故答案是:∠1=∠C或∠2=∠B或=,
14.解:有两种情形:
如图,当∠ADE=∠B时,△ADE∽△ABC,
∴,
∴,
∴AE=(cm),
当∠ADE′=∠C时,∵∠A=∠A,
∴△ADE′∽△ACB,
∴=,
∴,
∴AE′=1.5(cm),
故答案为:或1.5.
15.解:∵∠ACB=∠CBD=90°,
∴要使△ACB和△CBD相似,
必须或,
将AC=8,CB=2代入上式,得=或,
∴BD=或8.
∴当BD=或8时,图中的两个直角三角形相似.
故答案为:或8.
16.证明:∵AC2=AD AB,
∴AC:AB=AD:AC.
又∵∠A=∠A,
∴△ACD∽△ABC.
故理由是两边对应成比例及夹角相等,两三角形相似.
故答案为:两边对应成比例及夹角相等,两三角形相似.
17.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△AEF∽△DCF,△AEF∽△BEC,
∴△BEC∽△DCF,
故图中三对相似三角形.
故答案为:三.
18.解:矩形ABCD中,DC=AB=2,AD=BC=1,
又∵∠DAE=∠BAC,∠D=∠B,
∴△ADE∽△ABC,
∴AB:AD=BC:DE,
∴=,
∴DE=,
∴EC=DC﹣DE=.
故答案为:.
19.解:由图可知∠A为两个要证明相似的三角形的公共角,
因此,只要再找出一组对应角相等,或两组对应边成比例即可证明△ABC∽△ACD.
而①②④分别与∠A为△ABC与△ACD的公共角相结合,均可推出△ABC∽△ACD.
③中∠A不是已知的比例线段的夹角,故不正确.
∴选①②④.
故答案为:①②④.
20.解:如图所示,∵∠ABC=70°,BD平分∠ABC,
∴∠ABD=∠DBC,
又∵对角线BD是它的相似对角线,
∴△ABD∽△DBC,
∴∠A=∠BDC,∠ADB=∠C,
∴∠A+∠C=∠ADC,
又∵∠A+∠C+∠ADC=360°﹣70°=290°,
∴∠ADC=145°,
故答案为:145.
21.解:设经过t秒时,以△QBP与△ABC相似,则AP=2t厘米,BP=(8﹣2t)厘米,BQ=4t厘米,
∵∠PBQ=∠ABC,
∴当=时,△BPQ∽△BAC,即=,解得t=2(s);
当=时,△BPQ∽△BCA,即=,解得t=0.8(s);
即经过2秒或0.8秒时,△QBP与△ABC相似.
22.(1)证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF;
(2)E是中点时,∠BAE=∠EAF,
理由如下:
连接AF,延长AE于DC的延长线相交于点H,
∵E为BC中点,
∴BE=CE,
∵AB∥DH,
∴∠B=∠ECH,
∵∠AEB=∠CEH,
∴△ABE≌△HCE,
∴AE=EH,
∵EF⊥AH,
∴△AFH是等腰三角形,
∴∠EAF=∠H,
∵AB∥DH,
∴∠H=∠BAE,
∴∠BAE=∠EAF,
∴当点E在BC中点位置时,∠BAE=∠EAF.
23.解:(1)△ABE与△ADF相似.理由如下:
∵四边形ABCD为矩形,DF⊥AE,
∴∠ABE=∠AFD=90°,
∠AEB=∠DAF,
∴△ABE∽△DFA.
(2)∵△ABE∽△ADF
∴=,
∵在Rt△ABE中,AB=6,BE=8,
∴AE=10
∴DF===7.2.
答:DF的长为7.2.
24.(1)解:如图,射线BD即为所求;
(2)证明:在△ABC中,
∵∠A+∠ABC+∠ACB=180°,AB=AC,∠A=36°,
∴∠ABC=∠ACB=(180°﹣∠A)=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=ABC=×72°=36°,
∴∠CBD=∠CAB,
∵∠BCD=∠ACB,
∴△BDC∽△ABC.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
