第六章 反比例函数 专项训练A2021-2022学年北师大版九年级数学上册期末章节总复习(word版含答案)
文档属性
| 名称 | 第六章 反比例函数 专项训练A2021-2022学年北师大版九年级数学上册期末章节总复习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 510.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览


文档简介
北师大版九年级数学上学期期末章节总复习 第六章 反比例函数 专项训练A(含答案)
姓名:___________班级:___________
一、单选题
1.(2021·河北路北·九年级期末)若反比例函数y=图象经过点(5,-1),该函数图象在( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
2.(2021·河北双桥·九年级期末)若双曲线y=位于第二、四象限,则k的取值范围是( )
A.k<1 B.k≥1 C.k>1 D.k≠1
3.(2021·辽宁新抚·九年级期末)对于反比例函数,下列说法中不正确的是( )
A.点在它的图象上 B.它的图象在第一、三象限
C.随的增大而减小 D.当时,随的增大而减小
4.(2021·山东·泰安市黄前中学九年级期末)若点都在反比例函数的图象上,则的大小关系是( )
A. B. C. D.
5.(2021·湖南涟源·九年级期末)已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示.则这个反比例函数的解析式为( )
A. B. C. D.
6.(2021·河北高邑·九年级期末)已知函数是反比例函数,则此反比例函数的图象在( )
A.第一、三象限 B.第二、四象限
C.第一、四象限 D.第二、三象限
7.(2021·内蒙古磴口·九年级期末)一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
8.(2021·山东莱西·八年级期末)函数与()在同一坐标系中的图象可能是( )
A. B. C. D.
9.(2021·云南普洱·九年级期末)已知正比例函数的图象与反比例函数图象相交于点,下列说法正确的是( )
A.反比例函数的解析式是 B.两个函数图象的另一交点坐标为
C.当或时, D.正比例函数与反比例函数都随的增大而增大
10.(2021·山东蓬莱·八年级期末)已知点,,都在反比例函数的图像上,且,则,,的大小关系是( )
A. B. C. D.
11.(2021·广东茂名·九年级期末)已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )
A.y= B.y=﹣ C.y= D.y=﹣
12.(2021·福建涵江·九年级期末)如图,点在双曲线上,点在双曲线上,轴,过点作轴于.连接,与相交于点,若,则的值为( )
A.6 B.9 C.10 D.12
13.(2021·河南睢县·九年级期末)已知A(,),B(2,)两点在双曲线上,且,则m的取
值范围是( )
A. B. C. D.
14.(2021·河北高邑·九年级期末)一次函数y=ax+b与反比例函数,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
A.B.C. D.
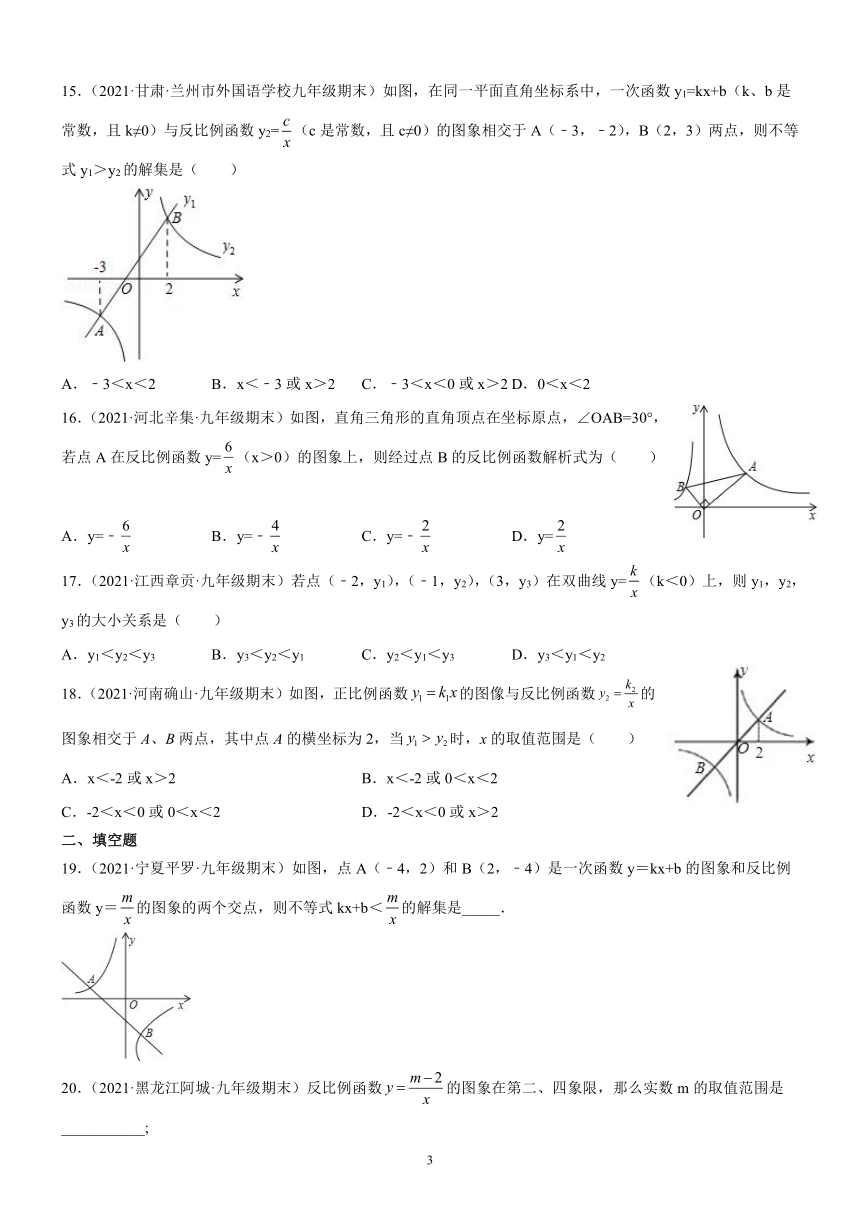
15.(2021·甘肃·兰州市外国语学校九年级期末)如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )
A.﹣3<x<2 B.x<﹣3或x>2 C.﹣3<x<0或x>2 D.0<x<2
16.(2021·河北辛集·九年级期末)如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=(x>0)的图象上,则经过点B的反比例函数解析式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=
17.(2021·江西章贡·九年级期末)若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y=(k<0)上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y2<y1<y3 D.y3<y1<y2
18.(2021·河南确山·九年级期末)如图,正比例函数的图像与反比例函数的图象相交于A、B两点,其中点A的横坐标为2,当时,x的取值范围是( )
A.x<-2或x>2 B.x<-2或0<x<2
C.-2<x<0或0<x<2 D.-2<x<0或x>2
二、填空题
19.(2021·宁夏平罗·九年级期末)如图,点A(﹣4,2)和B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点,则不等式kx+b<的解集是_____.
20.(2021·黑龙江阿城·九年级期末)反比例函数的图象在第二、四象限,那么实数m的取值范围是___________;
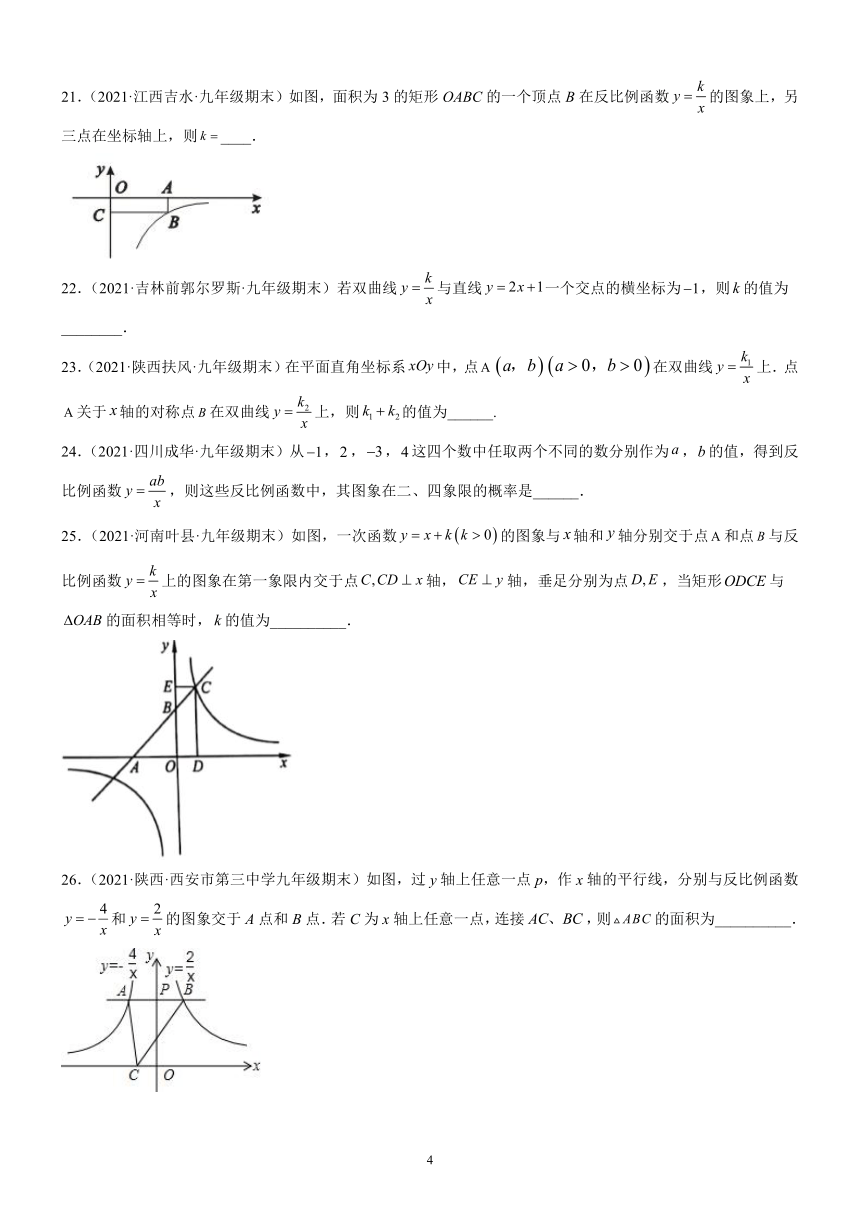
21.(2021·江西吉水·九年级期末)如图,面积为3的矩形OABC的一个顶点B在反比例函数的图象上,另三点在坐标轴上,则____.
22.(2021·吉林前郭尔罗斯·九年级期末)若双曲线与直线一个交点的横坐标为,则的值为________.
23.(2021·陕西扶风·九年级期末)在平面直角坐标系中,点在双曲线上.点关于轴的对称点在双曲线上,则的值为______.
24.(2021·四川成华·九年级期末)从,,,这四个数中任取两个不同的数分别作为,的值,得到反比例函数,则这些反比例函数中,其图象在二、四象限的概率是______.
25.(2021·河南叶县·九年级期末)如图,一次函数的图象与轴和轴分别交于点和点与反比例函数上的图象在第一象限内交于点轴,轴,垂足分别为点,当矩形与的面积相等时,的值为__________.
26.(2021·陕西·西安市第三中学九年级期末)如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数和的图象交于A点和B点.若C为x轴上任意一点,连接,则的面积为__________.
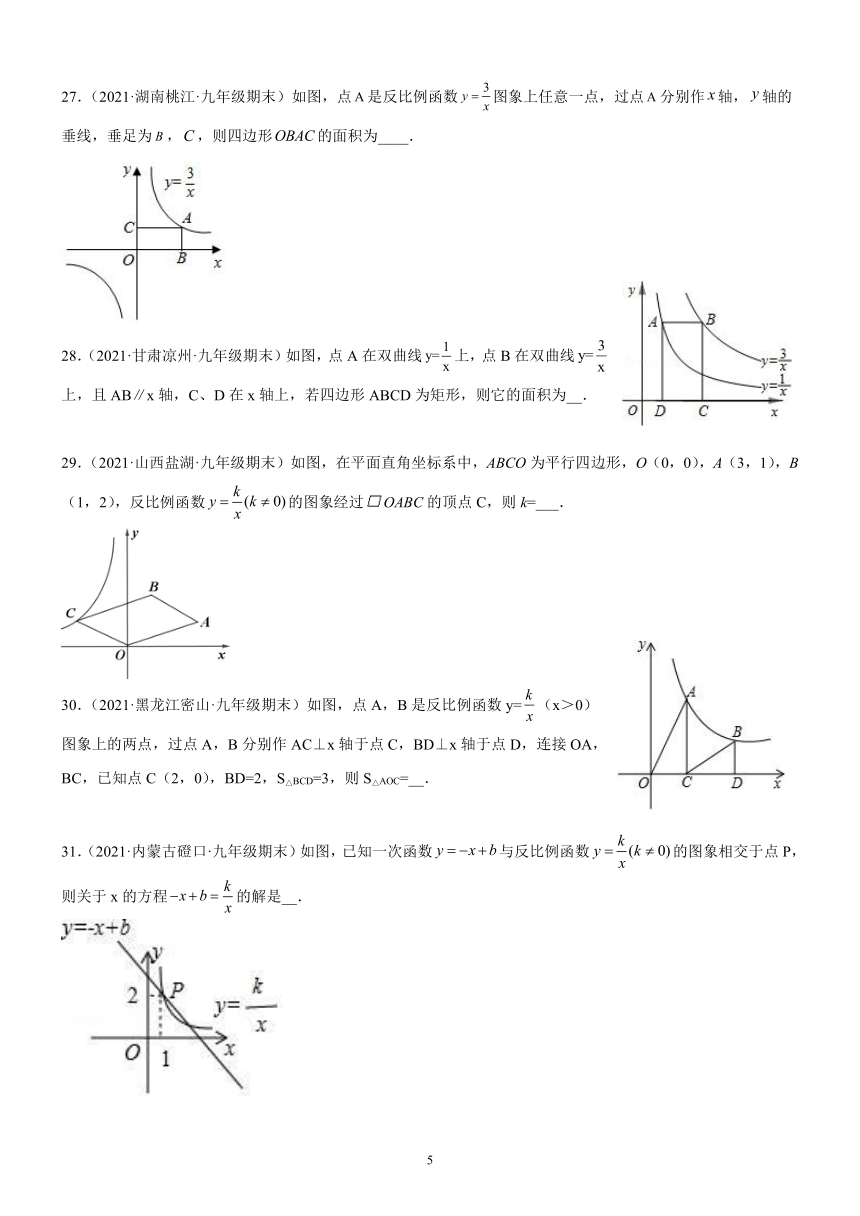
27.(2021·湖南桃江·九年级期末)如图,点是反比例函数图象上任意一点,过点分别作轴,轴的垂线,垂足为,,则四边形的面积为____.
28.(2021·甘肃凉州·九年级期末)如图,点A在双曲线上,点B在双曲线上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__.
29.(2021·山西盐湖·九年级期末)如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数的图象经过OABC的顶点C,则k=___.
30.(2021·黑龙江密山·九年级期末)如图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA,BC,已知点C(2,0),BD=2,S△BCD=3,则S△AOC=__.
31.(2021·内蒙古磴口·九年级期末)如图,已知一次函数与反比例函数的图象相交于点P,则关于x的方程的解是__.
32.(2021·云南盘龙·九年级期末)如图,在平面直角坐标系中,点在第一象限,轴于点,反比例函数的图象与线段相交于点,且是线段的中点,若的面积为3,则的值为__________.
33.(2021·山东·泰安市黄前中学九年级期末)如图,点A在反比例函数y=(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若=,△AOB的面积为6,则k的值为_____.
三、解答题
34.(2021·全国·九年级期末)如图,一次函数y1=x+b的图象与与反比例函数y2=(k≠0,x<0)的图象交于点A(﹣2,1),B两点.
(1)求一次函数与反比例函数的表达式;
(2)求△AOB的面积.
35.(2021·广西平果·九年级期末)如图,一次函数y1=x+2的图象与反比例函数y2=(k≠0)的图象交于A、B两点,且点A的坐标为(1,m).
(1)求反比例函数的表达式及点B的坐标;
(2)根据图象直接写出当y1>y2时x的取值范围.
36.(2021·四川渠县·九年级期末)心理学家研究发现,一般情况下,一节课40分钟,学生的注意力随教师讲课时间的变化而变化.学生的注意力指数y随时间x(分)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)上课后的第5分钟与第30分钟相比较,_______分钟时学生的注意力更集中.
(2)分别求出线段AB和双曲线CD的函数关系式.
(3)一道数学题,需要讲18分钟,为了学生听课效果较好,要求学生的注意力指数不低于40,那么经过适当的时间安排,教师能否在学生注意力达到所需状态下讲完这道题?
37.(2021·河南滑县·九年级期末)如图,一次函数的图象和反比例函数的图象相交于两点.
(1)试确定一次函数与反比例函数的解析式;
(2)求的面积;
(3)结合图象,直接写出使成立的的取值范围.
38.(2021·贵州织金·九年级期末)如图,一次函数的图象与反比例函数的图象交于两点,与交于点,点的坐标为.点的坐标为,连接.
(1)求一次函数与反比例函数的表达式;
(2)求点坐标和的面积;
(3)直接写出时自变量的取值范围.
39.(2021·湖南绥宁·九年级期末)已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
40.(2021·安徽太湖·九年级期末)如图,直线y1=﹣x+4,y2=x+b都与双曲线y=交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式x+b>的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.
参考答案
1.D 2.A 3.C 4.B 5.C 6.A 7.A 8.D 9.C 10.A 11.D 12.B
13.D 14.C 15.C 16.C 17.D 18.D
19.x>2或 4<x<0.
20.m<2
21.-3
22.1
23.0.
24.
25.
26.3
27.3
28.2
29.-2
30.5.
31.,
32.3
33.6
34.(1)一次函数的表达式是y1=x+3,反比例函数的表达式y2=﹣;(2)
35.(1)y=,B(﹣3,﹣1);(2)﹣3<x<0或x>1
36.(1)5;(2);.(3)教师能在学生注意力达到所需要求状态下讲完这道题.
37.(1)反比例函数的解析式为,一次函数的解析式为;(2)8;(3)或.
38.(1),;(2),8;(3)或.
39.(1)反比例函数解析式为y=﹣,一次函数的解析式为y=﹣x﹣2;(2)6;(3)x<﹣4或0<x<2.
40.(1);(2)x>1;(3)P(﹣,0)或(,0)
姓名:___________班级:___________
一、单选题
1.(2021·河北路北·九年级期末)若反比例函数y=图象经过点(5,-1),该函数图象在( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
2.(2021·河北双桥·九年级期末)若双曲线y=位于第二、四象限,则k的取值范围是( )
A.k<1 B.k≥1 C.k>1 D.k≠1
3.(2021·辽宁新抚·九年级期末)对于反比例函数,下列说法中不正确的是( )
A.点在它的图象上 B.它的图象在第一、三象限
C.随的增大而减小 D.当时,随的增大而减小
4.(2021·山东·泰安市黄前中学九年级期末)若点都在反比例函数的图象上,则的大小关系是( )
A. B. C. D.
5.(2021·湖南涟源·九年级期末)已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示.则这个反比例函数的解析式为( )
A. B. C. D.
6.(2021·河北高邑·九年级期末)已知函数是反比例函数,则此反比例函数的图象在( )
A.第一、三象限 B.第二、四象限
C.第一、四象限 D.第二、三象限
7.(2021·内蒙古磴口·九年级期末)一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
8.(2021·山东莱西·八年级期末)函数与()在同一坐标系中的图象可能是( )
A. B. C. D.
9.(2021·云南普洱·九年级期末)已知正比例函数的图象与反比例函数图象相交于点,下列说法正确的是( )
A.反比例函数的解析式是 B.两个函数图象的另一交点坐标为
C.当或时, D.正比例函数与反比例函数都随的增大而增大
10.(2021·山东蓬莱·八年级期末)已知点,,都在反比例函数的图像上,且,则,,的大小关系是( )
A. B. C. D.
11.(2021·广东茂名·九年级期末)已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )
A.y= B.y=﹣ C.y= D.y=﹣
12.(2021·福建涵江·九年级期末)如图,点在双曲线上,点在双曲线上,轴,过点作轴于.连接,与相交于点,若,则的值为( )
A.6 B.9 C.10 D.12
13.(2021·河南睢县·九年级期末)已知A(,),B(2,)两点在双曲线上,且,则m的取
值范围是( )
A. B. C. D.
14.(2021·河北高邑·九年级期末)一次函数y=ax+b与反比例函数,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
A.B.C. D.
15.(2021·甘肃·兰州市外国语学校九年级期末)如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )
A.﹣3<x<2 B.x<﹣3或x>2 C.﹣3<x<0或x>2 D.0<x<2
16.(2021·河北辛集·九年级期末)如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=(x>0)的图象上,则经过点B的反比例函数解析式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=
17.(2021·江西章贡·九年级期末)若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y=(k<0)上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y2<y1<y3 D.y3<y1<y2
18.(2021·河南确山·九年级期末)如图,正比例函数的图像与反比例函数的图象相交于A、B两点,其中点A的横坐标为2,当时,x的取值范围是( )
A.x<-2或x>2 B.x<-2或0<x<2
C.-2<x<0或0<x<2 D.-2<x<0或x>2
二、填空题
19.(2021·宁夏平罗·九年级期末)如图,点A(﹣4,2)和B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点,则不等式kx+b<的解集是_____.
20.(2021·黑龙江阿城·九年级期末)反比例函数的图象在第二、四象限,那么实数m的取值范围是___________;
21.(2021·江西吉水·九年级期末)如图,面积为3的矩形OABC的一个顶点B在反比例函数的图象上,另三点在坐标轴上,则____.
22.(2021·吉林前郭尔罗斯·九年级期末)若双曲线与直线一个交点的横坐标为,则的值为________.
23.(2021·陕西扶风·九年级期末)在平面直角坐标系中,点在双曲线上.点关于轴的对称点在双曲线上,则的值为______.
24.(2021·四川成华·九年级期末)从,,,这四个数中任取两个不同的数分别作为,的值,得到反比例函数,则这些反比例函数中,其图象在二、四象限的概率是______.
25.(2021·河南叶县·九年级期末)如图,一次函数的图象与轴和轴分别交于点和点与反比例函数上的图象在第一象限内交于点轴,轴,垂足分别为点,当矩形与的面积相等时,的值为__________.
26.(2021·陕西·西安市第三中学九年级期末)如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数和的图象交于A点和B点.若C为x轴上任意一点,连接,则的面积为__________.
27.(2021·湖南桃江·九年级期末)如图,点是反比例函数图象上任意一点,过点分别作轴,轴的垂线,垂足为,,则四边形的面积为____.
28.(2021·甘肃凉州·九年级期末)如图,点A在双曲线上,点B在双曲线上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__.
29.(2021·山西盐湖·九年级期末)如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数的图象经过OABC的顶点C,则k=___.
30.(2021·黑龙江密山·九年级期末)如图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA,BC,已知点C(2,0),BD=2,S△BCD=3,则S△AOC=__.
31.(2021·内蒙古磴口·九年级期末)如图,已知一次函数与反比例函数的图象相交于点P,则关于x的方程的解是__.
32.(2021·云南盘龙·九年级期末)如图,在平面直角坐标系中,点在第一象限,轴于点,反比例函数的图象与线段相交于点,且是线段的中点,若的面积为3,则的值为__________.
33.(2021·山东·泰安市黄前中学九年级期末)如图,点A在反比例函数y=(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若=,△AOB的面积为6,则k的值为_____.
三、解答题
34.(2021·全国·九年级期末)如图,一次函数y1=x+b的图象与与反比例函数y2=(k≠0,x<0)的图象交于点A(﹣2,1),B两点.
(1)求一次函数与反比例函数的表达式;
(2)求△AOB的面积.
35.(2021·广西平果·九年级期末)如图,一次函数y1=x+2的图象与反比例函数y2=(k≠0)的图象交于A、B两点,且点A的坐标为(1,m).
(1)求反比例函数的表达式及点B的坐标;
(2)根据图象直接写出当y1>y2时x的取值范围.
36.(2021·四川渠县·九年级期末)心理学家研究发现,一般情况下,一节课40分钟,学生的注意力随教师讲课时间的变化而变化.学生的注意力指数y随时间x(分)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)上课后的第5分钟与第30分钟相比较,_______分钟时学生的注意力更集中.
(2)分别求出线段AB和双曲线CD的函数关系式.
(3)一道数学题,需要讲18分钟,为了学生听课效果较好,要求学生的注意力指数不低于40,那么经过适当的时间安排,教师能否在学生注意力达到所需状态下讲完这道题?
37.(2021·河南滑县·九年级期末)如图,一次函数的图象和反比例函数的图象相交于两点.
(1)试确定一次函数与反比例函数的解析式;
(2)求的面积;
(3)结合图象,直接写出使成立的的取值范围.
38.(2021·贵州织金·九年级期末)如图,一次函数的图象与反比例函数的图象交于两点,与交于点,点的坐标为.点的坐标为,连接.
(1)求一次函数与反比例函数的表达式;
(2)求点坐标和的面积;
(3)直接写出时自变量的取值范围.
39.(2021·湖南绥宁·九年级期末)已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
40.(2021·安徽太湖·九年级期末)如图,直线y1=﹣x+4,y2=x+b都与双曲线y=交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式x+b>的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.
参考答案
1.D 2.A 3.C 4.B 5.C 6.A 7.A 8.D 9.C 10.A 11.D 12.B
13.D 14.C 15.C 16.C 17.D 18.D
19.x>2或 4<x<0.
20.m<2
21.-3
22.1
23.0.
24.
25.
26.3
27.3
28.2
29.-2
30.5.
31.,
32.3
33.6
34.(1)一次函数的表达式是y1=x+3,反比例函数的表达式y2=﹣;(2)
35.(1)y=,B(﹣3,﹣1);(2)﹣3<x<0或x>1
36.(1)5;(2);.(3)教师能在学生注意力达到所需要求状态下讲完这道题.
37.(1)反比例函数的解析式为,一次函数的解析式为;(2)8;(3)或.
38.(1),;(2),8;(3)或.
39.(1)反比例函数解析式为y=﹣,一次函数的解析式为y=﹣x﹣2;(2)6;(3)x<﹣4或0<x<2.
40.(1);(2)x>1;(3)P(﹣,0)或(,0)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
