沪科版数学八年级上册 11.1 平面内点的坐标 教案
文档属性
| 名称 | 沪科版数学八年级上册 11.1 平面内点的坐标 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 115.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览

文档简介
11.1平面直角坐标系(一)
一、教材分析:
平面直角坐标系的基本知识是学习全章及至以后数学学习的基础,在后面学习如何画函数图象以及研究一些具体函数图象的性质时,都要应用这些知识;它的建立,使代数的基本元素(数对)与几何的基本元素(点)之间产生一一对应,数发展成式、方程与函数,点运动而成直线、曲线等几何图形,于是实现了认识上从一维空间到二维空间的发展,构成更广阔的范围内的数形结合、互相转化的理论基础。因此,平面直角坐标系是沟通代数和几何的桥梁。
二、教学目标 :
(一)知识与技能 :
1、使学生了解平面直角坐标系的产生过程;
2、会正确画出平面直角坐标系;
3、使学生能在平面直角坐标系中,由点求坐标,由坐标描点;
(二)过程与方法 :
1、通过学生观察、思考、动手探索、分组讨论及总结,解决本节内容的相关问题及学生的疑问,使学生充分体会和掌握坐标系与点的关系;
2、通过理论与实践相结合,初步培养学生把实际问题抽象成数学模型的能力;
(三)情感与价值观 :
1、让学生体会数学来源于实践,反过来又指导实践进一步发展的辩证唯物主义思想。
2、通过教师的精心设计和引导,使学生在学习中合作,在合作中学习,让学生充分感受到团结的力量,培养学生实事求是的科学态度和积极参与、助人为乐的精神,同时使学生领会数学的严谨性和积极探索的精神。
三、教学重点难点 :
(一)教学重点 :
能在平面直角坐标系中,由点求坐标,由坐标描点。
教学难点 :
在平面直角坐标系中根据点的位置写出点的坐标,由坐标描出点。
四、教法学法 :
本节课以“问题情境──建立模型──巩固训练──拓展延伸”的模式展开,引导学生从已有的知识和生活经验出发,提出问题与学生共同探索、讨论解决问题的方法,让学生经历知识的形成与应用的过程,从而更好地理解数学知识的意义。
五、教学过程:
(一)问题引入
什么是数轴?
动手操作:在纸上任意画一条数轴。
1、规定了___、_____、______的直线叫做数轴。
2、数轴上的点与____一一对应。
3、写出数轴上A、B、C各点在数轴上的坐标。
(二)探究新知一:
探究1:想一想,在教室里,怎样确定一个同学的位置?
探究2:上电影院看电影,电影票上至少要有几个数据才能确定你的位置?
思考:怎样表示平面内的点的位置?
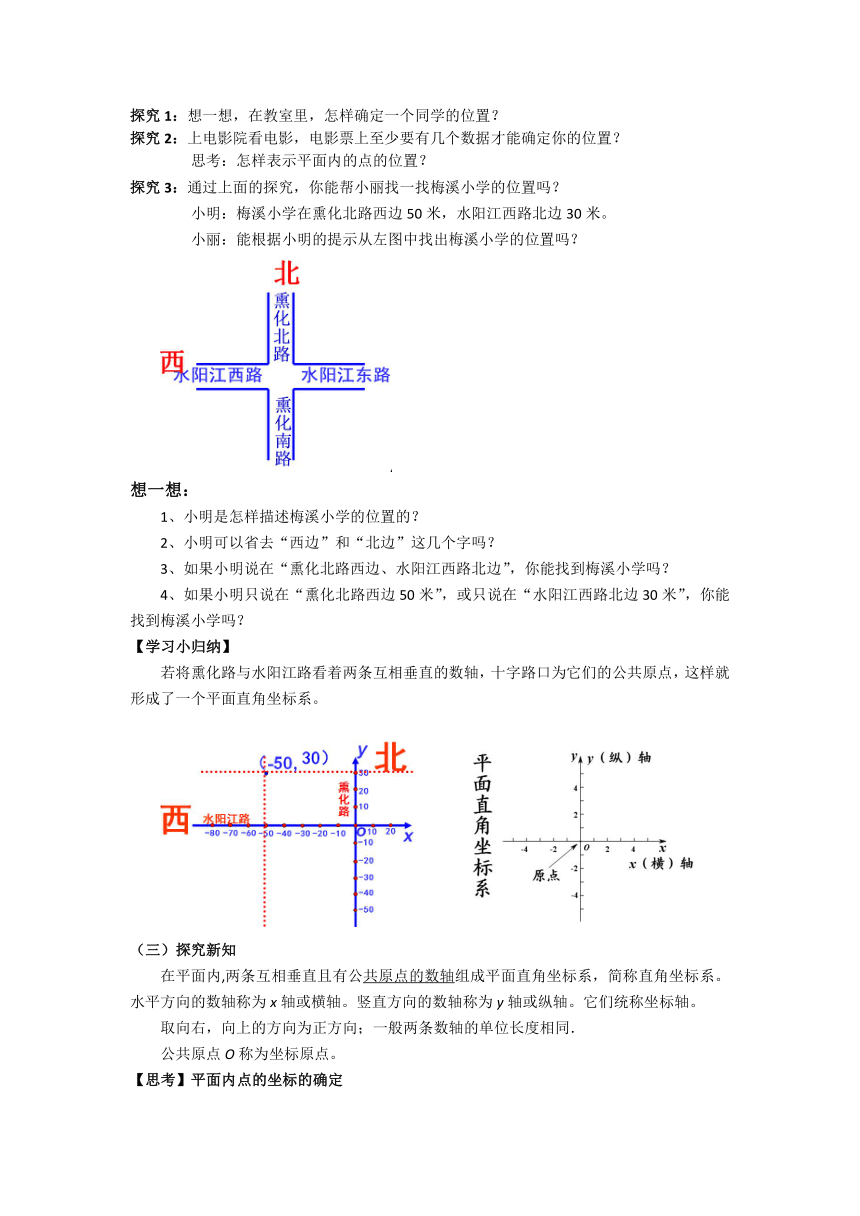
探究3:通过上面的探究,你能帮小丽找一找梅溪小学的位置吗?
小明:梅溪小学在熏化北路西边50米,水阳江西路北边30米。
小丽:能根据小明的提示从左图中找出梅溪小学的位置吗?
想一想:
小明是怎样描述梅溪小学的位置的?
小明可以省去“西边”和“北边”这几个字吗?
如果小明说在“熏化北路西边、水阳江西路北边”,你能找到梅溪小学吗?
如果小明只说在“熏化北路西边50米”,或只说在“水阳江西路北边30米”,你能找到梅溪小学吗?
【学习小归纳】
若将熏化路与水阳江路看着两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系。21教育网
(三)探究新知
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,简称直角坐标系。水平方向的数轴称为x轴或横轴。竖直方向的数轴称为y轴或纵轴。它们统称坐标轴。
取向右,向上的方向为正方向;一般两条数轴的单位长度相同.
公共原点O称为坐标原点。
【思考】平面内点的坐标的确定
平面内任意一点P,过P点分别向x、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点P的____、____,则有序数对(a,b)叫做点P的坐标。记为P(___,___)。21cnjy.com
注意:____写在前,____写在后,中间用逗号隔开。
练一练1:
如下左图,已知平面内一点Q,你能找到相应的一对有序实数在数轴上的位置吗?
过点Q分别作x轴,y轴的垂线,将垂足对应的数组合起来形成一对有序实数,即为点Q的坐标,可表示为Q(__,__)21·cn·jy·com
【思考】怎样确定点的位置
如上右图,在平面直角坐标系中,有序实数对(2,3)描述点P的位置,该如何确定点P的位置呢?
解析:过x轴上表示___的点作x轴的垂线,再过y轴上表示___的点作y轴的垂线,两线的___即为点P。www.21-cn-jy.com
练一练2:
1、在下左图平面直角坐标系中分别描出点A(3,2)、B(2,3)的位置,并写出点C、D、E的坐标。2·1·c·n·j·y
2、写出上面右图中A、B、C、D、E各点的坐标。
3、在上面右图直角坐标系中,描出下列各点:A(4,3),B(-2,3),C(-4,-1),D(2,-2)。【来源:21·世纪·教育·网】
(四)探究新知三
如下图,x轴和y轴把平面分成四个部分,分别叫做第一、二、三、四现象,各象限内的点的坐标符合分别为(___,___),(___,___),(___,___),(___,___),坐标轴上的点,也就是x轴、y轴上的点不属于任何一个现象。在x轴上的点,纵坐标等于___;在y轴上的点,横坐标等于________________。21·世纪*教育网
练一练3:
1、已知a<b<0,那么点P(a-b,-b)在第____象限。
2、已知P点坐标为(a+1,a-3)
①点P在x轴上,则a=____;
②点P在y轴上,则a=____。
3、若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为____________.
(五)课堂小结
1、如何建立平面直角坐标系?
2、点的坐标的表示,在坐标平面中找点的位置?
3、坐标平面内的点与有序实数对之间的关系
4、各象限内点及x轴、y轴上的点的坐标的特点。
六、板书设计:
11.1 平面直角坐标系(一)
七、教学设计说明:
本节课由于比较注重知识的产生发展过程,同时也有意识地渗透了一些数学文化,因此本节课中学生巩固训练的时间相对偏少
坐标系产生的必要性是难点,而坐标系知识对后续的学习又显得尤为重要,因此本节课中教师的课前准备与课堂组织显得尤其重要。本节课中,通过创设一些问题情境,积极引导、启发学生探索思考,使学生学会学习、学会探索、学会研究。同时,借助设计制作的多媒体课件辅助手段,极大地提高了课堂教学效益。因此,在本节课中,教师的主导作用得到较好的发挥。由于学生的个体差异表现为认知方式与思维策略的不同,以及认知水平和学习能力的差异,所以在整个教学过程中,都应尊重学生在解决问题过程中所表现出的不同水平,尽可能地让所有学生都能主动参与,并引导学生在与他人的交流中提高思维水平。在学生回答时,通过语言、目光、动作给予鼓励与赞许,发挥评价的积极功能。尤其注意鼓励学有困难的学生主动参与学习活动,发表自己看法,肯定他们的点滴进步。对出现的错误耐心引导他们分析其产生的原因,鼓励他们改进;对学生思维的闪光点及时“亮相”,并予以肯定鼓励;对学有余力并对数学有浓厚兴趣的同学,通过布置选做题与研究性课题作业去发展他们的数学才能。
一、教材分析:
平面直角坐标系的基本知识是学习全章及至以后数学学习的基础,在后面学习如何画函数图象以及研究一些具体函数图象的性质时,都要应用这些知识;它的建立,使代数的基本元素(数对)与几何的基本元素(点)之间产生一一对应,数发展成式、方程与函数,点运动而成直线、曲线等几何图形,于是实现了认识上从一维空间到二维空间的发展,构成更广阔的范围内的数形结合、互相转化的理论基础。因此,平面直角坐标系是沟通代数和几何的桥梁。
二、教学目标 :
(一)知识与技能 :
1、使学生了解平面直角坐标系的产生过程;
2、会正确画出平面直角坐标系;
3、使学生能在平面直角坐标系中,由点求坐标,由坐标描点;
(二)过程与方法 :
1、通过学生观察、思考、动手探索、分组讨论及总结,解决本节内容的相关问题及学生的疑问,使学生充分体会和掌握坐标系与点的关系;
2、通过理论与实践相结合,初步培养学生把实际问题抽象成数学模型的能力;
(三)情感与价值观 :
1、让学生体会数学来源于实践,反过来又指导实践进一步发展的辩证唯物主义思想。
2、通过教师的精心设计和引导,使学生在学习中合作,在合作中学习,让学生充分感受到团结的力量,培养学生实事求是的科学态度和积极参与、助人为乐的精神,同时使学生领会数学的严谨性和积极探索的精神。
三、教学重点难点 :
(一)教学重点 :
能在平面直角坐标系中,由点求坐标,由坐标描点。
教学难点 :
在平面直角坐标系中根据点的位置写出点的坐标,由坐标描出点。
四、教法学法 :
本节课以“问题情境──建立模型──巩固训练──拓展延伸”的模式展开,引导学生从已有的知识和生活经验出发,提出问题与学生共同探索、讨论解决问题的方法,让学生经历知识的形成与应用的过程,从而更好地理解数学知识的意义。
五、教学过程:
(一)问题引入
什么是数轴?
动手操作:在纸上任意画一条数轴。
1、规定了___、_____、______的直线叫做数轴。
2、数轴上的点与____一一对应。
3、写出数轴上A、B、C各点在数轴上的坐标。
(二)探究新知一:
探究1:想一想,在教室里,怎样确定一个同学的位置?
探究2:上电影院看电影,电影票上至少要有几个数据才能确定你的位置?
思考:怎样表示平面内的点的位置?
探究3:通过上面的探究,你能帮小丽找一找梅溪小学的位置吗?
小明:梅溪小学在熏化北路西边50米,水阳江西路北边30米。
小丽:能根据小明的提示从左图中找出梅溪小学的位置吗?
想一想:
小明是怎样描述梅溪小学的位置的?
小明可以省去“西边”和“北边”这几个字吗?
如果小明说在“熏化北路西边、水阳江西路北边”,你能找到梅溪小学吗?
如果小明只说在“熏化北路西边50米”,或只说在“水阳江西路北边30米”,你能找到梅溪小学吗?
【学习小归纳】
若将熏化路与水阳江路看着两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系。21教育网
(三)探究新知
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,简称直角坐标系。水平方向的数轴称为x轴或横轴。竖直方向的数轴称为y轴或纵轴。它们统称坐标轴。
取向右,向上的方向为正方向;一般两条数轴的单位长度相同.
公共原点O称为坐标原点。
【思考】平面内点的坐标的确定
平面内任意一点P,过P点分别向x、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点P的____、____,则有序数对(a,b)叫做点P的坐标。记为P(___,___)。21cnjy.com
注意:____写在前,____写在后,中间用逗号隔开。
练一练1:
如下左图,已知平面内一点Q,你能找到相应的一对有序实数在数轴上的位置吗?
过点Q分别作x轴,y轴的垂线,将垂足对应的数组合起来形成一对有序实数,即为点Q的坐标,可表示为Q(__,__)21·cn·jy·com
【思考】怎样确定点的位置
如上右图,在平面直角坐标系中,有序实数对(2,3)描述点P的位置,该如何确定点P的位置呢?
解析:过x轴上表示___的点作x轴的垂线,再过y轴上表示___的点作y轴的垂线,两线的___即为点P。www.21-cn-jy.com
练一练2:
1、在下左图平面直角坐标系中分别描出点A(3,2)、B(2,3)的位置,并写出点C、D、E的坐标。2·1·c·n·j·y
2、写出上面右图中A、B、C、D、E各点的坐标。
3、在上面右图直角坐标系中,描出下列各点:A(4,3),B(-2,3),C(-4,-1),D(2,-2)。【来源:21·世纪·教育·网】
(四)探究新知三
如下图,x轴和y轴把平面分成四个部分,分别叫做第一、二、三、四现象,各象限内的点的坐标符合分别为(___,___),(___,___),(___,___),(___,___),坐标轴上的点,也就是x轴、y轴上的点不属于任何一个现象。在x轴上的点,纵坐标等于___;在y轴上的点,横坐标等于________________。21·世纪*教育网
练一练3:
1、已知a<b<0,那么点P(a-b,-b)在第____象限。
2、已知P点坐标为(a+1,a-3)
①点P在x轴上,则a=____;
②点P在y轴上,则a=____。
3、若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为____________.
(五)课堂小结
1、如何建立平面直角坐标系?
2、点的坐标的表示,在坐标平面中找点的位置?
3、坐标平面内的点与有序实数对之间的关系
4、各象限内点及x轴、y轴上的点的坐标的特点。
六、板书设计:
11.1 平面直角坐标系(一)
七、教学设计说明:
本节课由于比较注重知识的产生发展过程,同时也有意识地渗透了一些数学文化,因此本节课中学生巩固训练的时间相对偏少
坐标系产生的必要性是难点,而坐标系知识对后续的学习又显得尤为重要,因此本节课中教师的课前准备与课堂组织显得尤其重要。本节课中,通过创设一些问题情境,积极引导、启发学生探索思考,使学生学会学习、学会探索、学会研究。同时,借助设计制作的多媒体课件辅助手段,极大地提高了课堂教学效益。因此,在本节课中,教师的主导作用得到较好的发挥。由于学生的个体差异表现为认知方式与思维策略的不同,以及认知水平和学习能力的差异,所以在整个教学过程中,都应尊重学生在解决问题过程中所表现出的不同水平,尽可能地让所有学生都能主动参与,并引导学生在与他人的交流中提高思维水平。在学生回答时,通过语言、目光、动作给予鼓励与赞许,发挥评价的积极功能。尤其注意鼓励学有困难的学生主动参与学习活动,发表自己看法,肯定他们的点滴进步。对出现的错误耐心引导他们分析其产生的原因,鼓励他们改进;对学生思维的闪光点及时“亮相”,并予以肯定鼓励;对学有余力并对数学有浓厚兴趣的同学,通过布置选做题与研究性课题作业去发展他们的数学才能。
