2021-2022学年高一下学期数学北师大版(2019)必修第二册1.8三角函数的简单应用 课件(共27张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册1.8三角函数的简单应用 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
§ 1.8 三角函数的简单应用
北师大(2019)必修2
聚焦知识目标
1.了解三角函数是研究周期现象最重要的模型.
2.初步体会如何利用三角函数研究简单的实际问题.
数学素养
通过三角函数的简单应用,培养数学运算与数学建模素养.
环节一
情境引入
情境引入
周期现象是自然界中最常见的现象之一,三角函数是研究周期现象最重要的数学模型,这一节将利用三角函数研究关于周期现象的简单的实际问题.
请欣赏:水车风情
情境引入
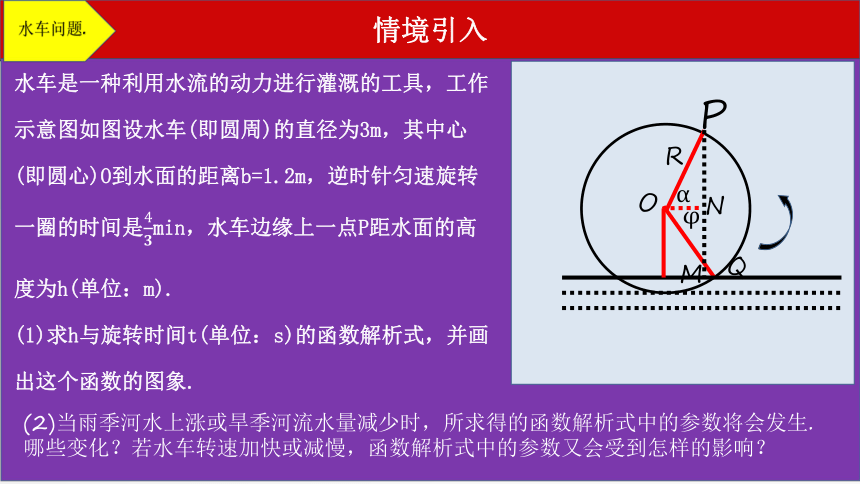
水车是一种利用水流的动力进行灌溉的工具,工作示意图如图设水车(即圆周)的直径为3m,其中心(即圆心)O到水面的距离b=1.2m,逆时针匀速旋转一圈的时间是min,水车边缘上一点P距水面的高度为h(单位:m).
(1)求h与旋转时间t(单位:s)的函数解析式,并画出这个函数的图象.
水车问题.
P
Q
N
O
M
R
α
(2)当雨季河水上涨或旱季河流水量减少时,所求得的函数解析式中的参数将会发生.哪些变化?若水车转速加快或减慢,函数解析式中的参数又会受到怎样的影响?
φ
解:设点P在水面上时高度h为0,当点P旋转到水面以下时,点P距水面的高度为负值.
(1)过点P向水面作垂线,交水面于点M,PM的长度为点P的高度h,过水车中心O,作PM的垂线.交PM于点N,设Q为水车与水面交点、△QON=φ.由已知,水车的半径R=1.5m,水车中心到水面的距离b=1.2m,水车旋转一圈所需的时间为T= 80s,转速为π/40rads.
不妨从水车与水面交点Q时开始计时(t=0),旋转ts水车转动的角的大小为α,即
情境引入
从图中不难看出:
h=PM=PN+NM=Rsin(α-φ)+b①
因为 所以φ≈53.1°=0.295πrad.因此
②
这就是点P距水面的高度h关于时间t的函数解析式.
水车问题.
P
Q
N
O
M
R
α
φ
情境引入
当点P旋转到与中心O等高时,点P到水面的距离恰好是1.2m.此时 0,t=40×0. 295=11.8(s).找出使t-0.295π取0. 的五个关键点,列表、描点,画出函数在区间[0,91.8]上的图象
水车问题.
P
Q
N
O
M
R
α
φ
11.8 31.8 51.8 71.8 91.8
1.2 1.2 2.7 1.2 -0.3 1.2
将造成水车中心O与水面距离的改变,导致函解析式中的参数b发生变化.水面上涨时参数b减小;水面回落时参数b增大.如果水车每速加快,将使周期T减小,转速减慢则使周期T增大.
环节二
三角函数建模
三角函数建模问题
面对实际问题建立数学模型,是一项重要的基本技能,这个过程并不神秘,就像这个例子题,把问题提供的“条件”逐条地“翻译”成“数学语言”是很自然的.
建模步骤
审清题意读懂题目中的“文字”“图象”“符号等语言,理解所反映的实际问题的背景,提炼出相应的数学问题
建立函数模型,整理数据,引入变量,找出变化规律,运用已掌握的三角函数知识、物理知识及其他相关知识建立关系式,即建立三角函数模型
解答函数模型:利用所学的三角函数知识解答得到的三角函数模型,求得结果
得出结论,将所得结论翻译成实际问题的答案
三角函数建模问题
来源于生活
1.已知某海滨浴场的海浪高度y(米)是时间t(时)的函数,其中0≤t≤24,记y=f(t),下表是某日各时的浪高数据:
t 0 3 6 9 12 15 18 21 24
y 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
经长期观测,y=f(t)的图象可近似地看成是函数y=Acos ωt+b的图象.
(1)根据以上数据,求其最小正周期,振幅及函数解析式;
(2)根据规定,当海浪高度大于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的8:00到20:00之间有多少时间可供冲浪者进行活动
(1)根据y的最大值和最小值求A,b,周期及ω.
(2)解不等式y>1,确定有多少时间可供冲浪者活动.
三角函数建模问题
练习
1.某昆虫种群数量1月1日低到700只,其数量随着时间变化逐渐增加,到当年7月1日高达900只,其数量在这两个值之间按正弦曲线规律改变.
(1)求出这种昆虫种群数量y(单位:只)关于时间t(单位:月)的函数解析式;
(2)画出这个函数的图象.
三角函数建模问题
来源于物理
2.交流电的电压E(单位:V)与时间t(单位:s)的关系可用E=220·sin来表示,求:
(1)开始时电压;
(2)电压值重复出现一次的时间间隔;
(3)电压的最大值和第一次获得最大值的时间.
[思路点拨]交流电压与时间的关系呈现周期性变化,t=0时即为初始电压,求周期和最值可直接运用性质.
三角函数建模问题
来源于物理
[解](1)当t=0时, =110√3 ( ),即开始时的电压为 110√3 .(2) =2 /100 =1/50 ( ),即时间间隔为0.02s.
(3)电压的最大值为 220√3 .
当 100 + /6= /2即 =1/300 时第一次取得最大值.
解后心得
来源于物理
三角函数模型处理物理学问题的策略
(1)常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期性;
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
三角函数建模问题
练习
2.单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系为s=6sin.
(1)单摆开始摆动时,离开平衡位置多少厘米?
(2)单摆摆动到最右边时,离开平衡位置多少厘米?
(3)单摆来回摆动一次需要多少时间?
环节三
学习与反思
1、电流I(单位:A)随时间t(单位:s)变化的函数解析式是I=Asinωt、t∈[0,+∞),其中ω=10πrad/s,A=5.
(1)求电流I变化的周期;
(2)当 时,求电流I.
2.一个单摆如图所示,小球偏离铅垂线方向的角为a rad,a与摆动时间t(单位:s)之间的函数解析式为 求
(1)最初(t=0)时a的值;
(2)单摆摆动的频率;
(3)经过多长时间单摆完成5次完整摆动
3.如图,挂在弹簧下方的小球做上下振动,小球在时间t(单位:s)时相对于平衡位置(即静止的位置)的高度为h(单位:cm),由下列关系式决定:∞)
以横轴表示时间,纵轴表示高度,画出这个函数在一个周期的闭区间上的简图,并回答下列问题:
(1)小球开始振动(t=0)时的位置在哪里
(2)小球位于最高、最低位置时h的值是多少
(3)经过多长时间小球振动一次(即周期是多少)
4.某地为发展旅游业,在旅游手册中给出了当地一年每个月的月平均气温表,根据图中提供的数据,试用 近似地拟合出月平均气温y(单位:℃)与时间t(单位:月)的函数关系,并求:出其周期和振幅,以及气温达到最大值和最小值的时间.(答案不唯一)
§ 1.8 三角函数的简单应用
北师大(2019)必修2
聚焦知识目标
1.了解三角函数是研究周期现象最重要的模型.
2.初步体会如何利用三角函数研究简单的实际问题.
数学素养
通过三角函数的简单应用,培养数学运算与数学建模素养.
环节一
情境引入
情境引入
周期现象是自然界中最常见的现象之一,三角函数是研究周期现象最重要的数学模型,这一节将利用三角函数研究关于周期现象的简单的实际问题.
请欣赏:水车风情
情境引入
水车是一种利用水流的动力进行灌溉的工具,工作示意图如图设水车(即圆周)的直径为3m,其中心(即圆心)O到水面的距离b=1.2m,逆时针匀速旋转一圈的时间是min,水车边缘上一点P距水面的高度为h(单位:m).
(1)求h与旋转时间t(单位:s)的函数解析式,并画出这个函数的图象.
水车问题.
P
Q
N
O
M
R
α
(2)当雨季河水上涨或旱季河流水量减少时,所求得的函数解析式中的参数将会发生.哪些变化?若水车转速加快或减慢,函数解析式中的参数又会受到怎样的影响?
φ
解:设点P在水面上时高度h为0,当点P旋转到水面以下时,点P距水面的高度为负值.
(1)过点P向水面作垂线,交水面于点M,PM的长度为点P的高度h,过水车中心O,作PM的垂线.交PM于点N,设Q为水车与水面交点、△QON=φ.由已知,水车的半径R=1.5m,水车中心到水面的距离b=1.2m,水车旋转一圈所需的时间为T= 80s,转速为π/40rads.
不妨从水车与水面交点Q时开始计时(t=0),旋转ts水车转动的角的大小为α,即
情境引入
从图中不难看出:
h=PM=PN+NM=Rsin(α-φ)+b①
因为 所以φ≈53.1°=0.295πrad.因此
②
这就是点P距水面的高度h关于时间t的函数解析式.
水车问题.
P
Q
N
O
M
R
α
φ
情境引入
当点P旋转到与中心O等高时,点P到水面的距离恰好是1.2m.此时 0,t=40×0. 295=11.8(s).找出使t-0.295π取0. 的五个关键点,列表、描点,画出函数在区间[0,91.8]上的图象
水车问题.
P
Q
N
O
M
R
α
φ
11.8 31.8 51.8 71.8 91.8
1.2 1.2 2.7 1.2 -0.3 1.2
将造成水车中心O与水面距离的改变,导致函解析式中的参数b发生变化.水面上涨时参数b减小;水面回落时参数b增大.如果水车每速加快,将使周期T减小,转速减慢则使周期T增大.
环节二
三角函数建模
三角函数建模问题
面对实际问题建立数学模型,是一项重要的基本技能,这个过程并不神秘,就像这个例子题,把问题提供的“条件”逐条地“翻译”成“数学语言”是很自然的.
建模步骤
审清题意读懂题目中的“文字”“图象”“符号等语言,理解所反映的实际问题的背景,提炼出相应的数学问题
建立函数模型,整理数据,引入变量,找出变化规律,运用已掌握的三角函数知识、物理知识及其他相关知识建立关系式,即建立三角函数模型
解答函数模型:利用所学的三角函数知识解答得到的三角函数模型,求得结果
得出结论,将所得结论翻译成实际问题的答案
三角函数建模问题
来源于生活
1.已知某海滨浴场的海浪高度y(米)是时间t(时)的函数,其中0≤t≤24,记y=f(t),下表是某日各时的浪高数据:
t 0 3 6 9 12 15 18 21 24
y 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
经长期观测,y=f(t)的图象可近似地看成是函数y=Acos ωt+b的图象.
(1)根据以上数据,求其最小正周期,振幅及函数解析式;
(2)根据规定,当海浪高度大于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的8:00到20:00之间有多少时间可供冲浪者进行活动
(1)根据y的最大值和最小值求A,b,周期及ω.
(2)解不等式y>1,确定有多少时间可供冲浪者活动.
三角函数建模问题
练习
1.某昆虫种群数量1月1日低到700只,其数量随着时间变化逐渐增加,到当年7月1日高达900只,其数量在这两个值之间按正弦曲线规律改变.
(1)求出这种昆虫种群数量y(单位:只)关于时间t(单位:月)的函数解析式;
(2)画出这个函数的图象.
三角函数建模问题
来源于物理
2.交流电的电压E(单位:V)与时间t(单位:s)的关系可用E=220·sin来表示,求:
(1)开始时电压;
(2)电压值重复出现一次的时间间隔;
(3)电压的最大值和第一次获得最大值的时间.
[思路点拨]交流电压与时间的关系呈现周期性变化,t=0时即为初始电压,求周期和最值可直接运用性质.
三角函数建模问题
来源于物理
[解](1)当t=0时, =110√3 ( ),即开始时的电压为 110√3 .(2) =2 /100 =1/50 ( ),即时间间隔为0.02s.
(3)电压的最大值为 220√3 .
当 100 + /6= /2即 =1/300 时第一次取得最大值.
解后心得
来源于物理
三角函数模型处理物理学问题的策略
(1)常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期性;
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
三角函数建模问题
练习
2.单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系为s=6sin.
(1)单摆开始摆动时,离开平衡位置多少厘米?
(2)单摆摆动到最右边时,离开平衡位置多少厘米?
(3)单摆来回摆动一次需要多少时间?
环节三
学习与反思
1、电流I(单位:A)随时间t(单位:s)变化的函数解析式是I=Asinωt、t∈[0,+∞),其中ω=10πrad/s,A=5.
(1)求电流I变化的周期;
(2)当 时,求电流I.
2.一个单摆如图所示,小球偏离铅垂线方向的角为a rad,a与摆动时间t(单位:s)之间的函数解析式为 求
(1)最初(t=0)时a的值;
(2)单摆摆动的频率;
(3)经过多长时间单摆完成5次完整摆动
3.如图,挂在弹簧下方的小球做上下振动,小球在时间t(单位:s)时相对于平衡位置(即静止的位置)的高度为h(单位:cm),由下列关系式决定:∞)
以横轴表示时间,纵轴表示高度,画出这个函数在一个周期的闭区间上的简图,并回答下列问题:
(1)小球开始振动(t=0)时的位置在哪里
(2)小球位于最高、最低位置时h的值是多少
(3)经过多长时间小球振动一次(即周期是多少)
4.某地为发展旅游业,在旅游手册中给出了当地一年每个月的月平均气温表,根据图中提供的数据,试用 近似地拟合出月平均气温y(单位:℃)与时间t(单位:月)的函数关系,并求:出其周期和振幅,以及气温达到最大值和最小值的时间.(答案不唯一)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
