5.1 第1课时 相交线-人教版七年级数学下册同步练习(word版含答案)
文档属性
| 名称 | 5.1 第1课时 相交线-人教版七年级数学下册同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 260.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 12:04:36 | ||
图片预览


文档简介
5.1 相交线
第1课时 相交线
1.如图,直线m和n相交于点O,若∠1=40°,则∠2的度数是( )
A.40° B.50° C.140° D.150°
如图所示中,∠1与∠2是邻补角的是( )
A B C D
3.若∠1=64°,则∠1的邻补角度数为 .
4.在下面四个图形中,∠1与∠2是对顶角的是( )
A B C D
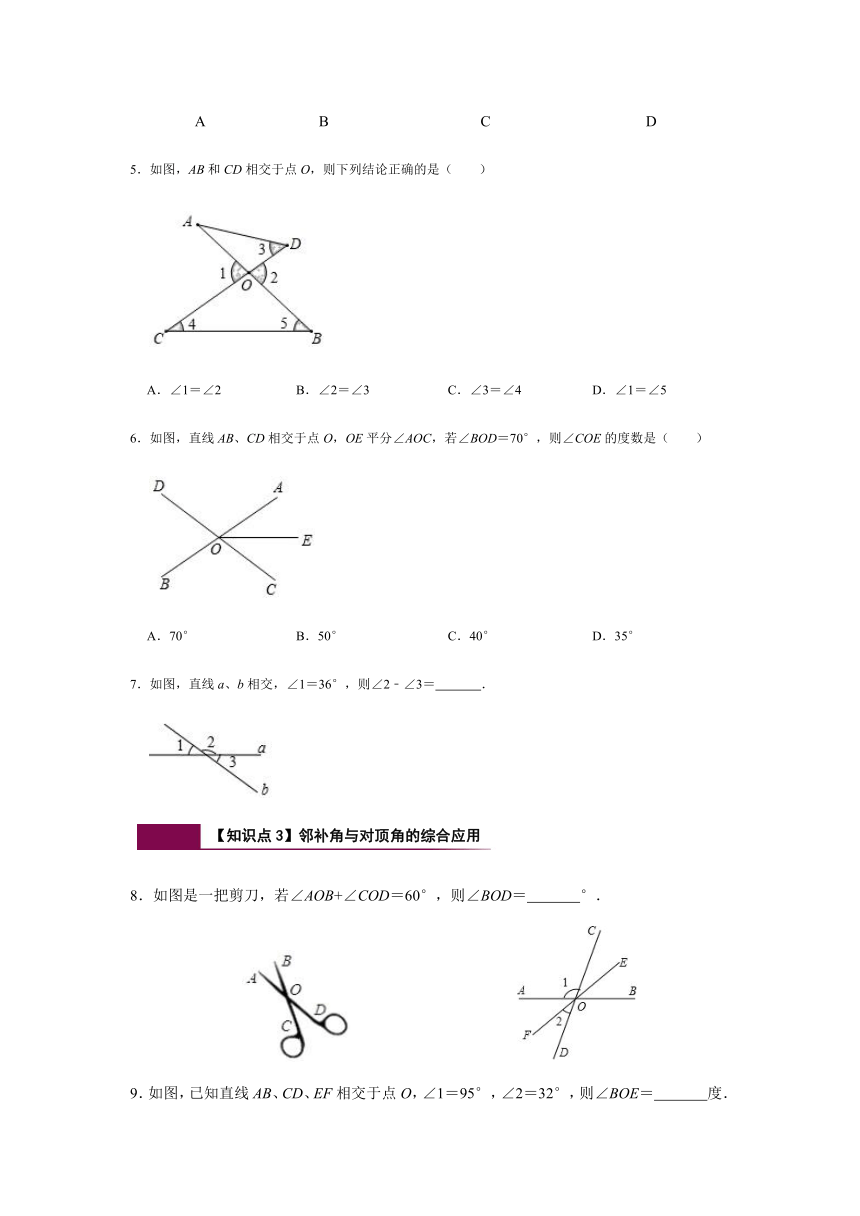
5.如图,AB和CD相交于点O,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠1=∠5
6.如图,直线AB、CD相交于点O,OE平分∠AOC,若∠BOD=70°,则∠COE的度数是( )
A.70° B.50° C.40° D.35°
7.如图,直线a、b相交,∠1=36°,则∠2﹣∠3= .
8.如图是一把剪刀,若∠AOB+∠COD=60°,则∠BOD= °.
9.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE= 度.
10.有以下5个说法:①两点之间,线段最短:②相等的角是对顶角:③互补的两个角中必定一个是锐角一个钝角;④两个锐角的和一定是锐角:⑤同角或等角的余角相等.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
11.如图,直线AB、CD相交于点O,∠BOE=90°,OF平分∠AOE,∠1=15°30′,则下列结论不正确的是( )
A.∠2=45° B.∠1=∠3
C.∠AOD+∠1=180° D.∠EOD=75°30'
12.在一个三角形中,一个外角是其相邻内角的2倍,那么这个外角是( )
A.150 B.120° C.100° D.90°
13.如图,直线AB、CD相交于点O,下列描述:
①∠1和∠2互为对顶角;②∠1和∠2互为邻补角;③∠1=∠2;④∠1=∠3
其中正确的是( )
A.①③ B.②④ C.②③ D.①④
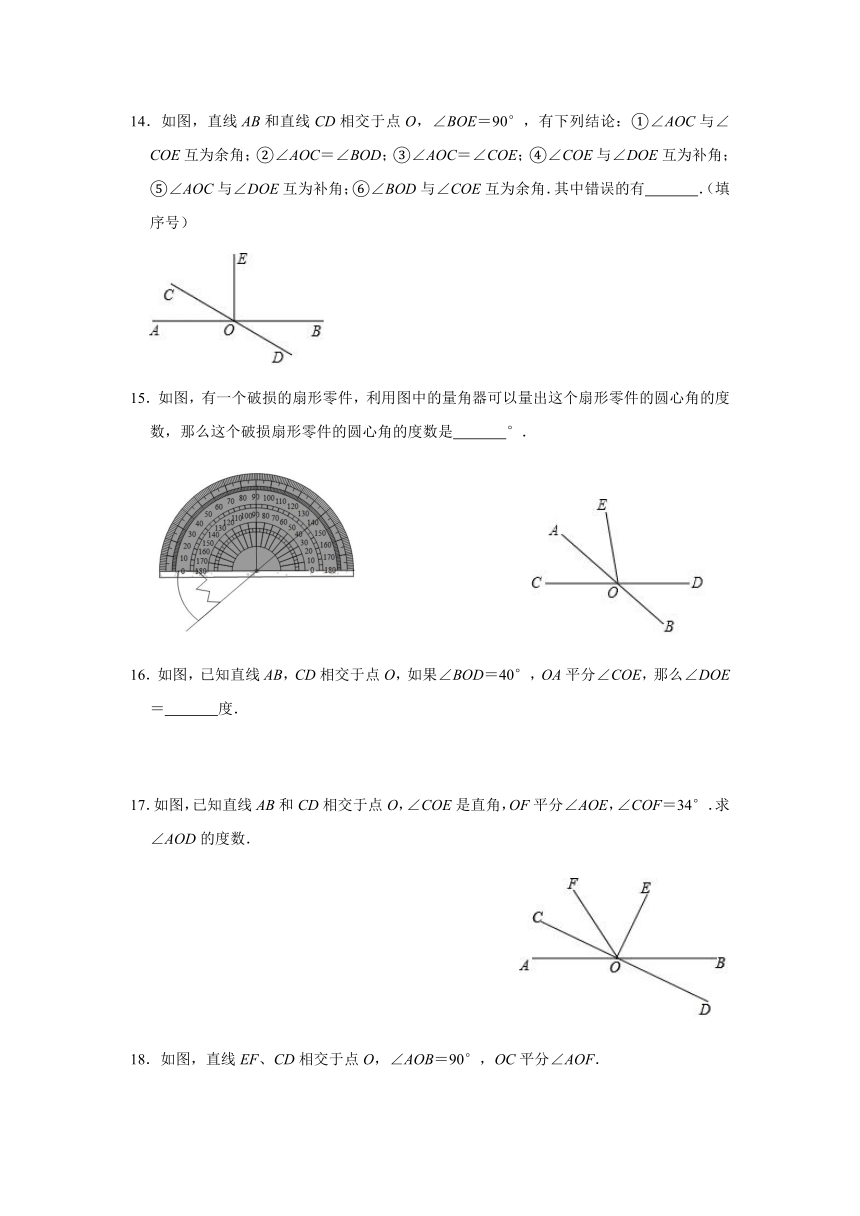
14.如图,直线AB和直线CD相交于点O,∠BOE=90°,有下列结论:①∠AOC与∠COE互为余角;②∠AOC=∠BOD;③∠AOC=∠COE;④∠COE与∠DOE互为补角;⑤∠AOC与∠DOE互为补角;⑥∠BOD与∠COE互为余角.其中错误的有 .(填序号)
15.如图,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,那么这个破损扇形零件的圆心角的度数是 °.
16.如图,已知直线AB,CD相交于点O,如果∠BOD=40°,OA平分∠COE,那么∠DOE= 度.
17.如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE,∠COF=34°.求∠AOD的度数.
18.如图,直线EF、CD相交于点O,∠AOB=90°,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)、(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
19.如图,直线AB、CD相交于O,∠EOC=90°,OF是∠AOE的角平分线,∠COF=34°,求∠BOD的度数.
其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
解:∵∠EOC=90°
∠COF=34°( )
∴∠EOF= °
∵OF是∠AOE的角平分线
∴∠AOF= =56°( )
∴∠AOC= °
∵∠AOC+ =90°
∠BOO+∠EOB=90°
∴∠BOD=∠AOC= °( )
20.直线AB、CD相交于点O,∠EOF在∠AOD的内部.
(1)如图①,当∠AOD=150°,∠EOF=30°时,求∠AOF与∠EOD的度数和;
(2)在(1)的条件下,请直接写出图中与∠BOC互补的角;
(3)如图②,若射线OM平分∠AOD(OM在∠EOD内部),且满足∠EOD=2∠FOM,请判断∠AOF与∠EOF的大小关系并说明理由.
参考答案
1.C.2.D.3.116°.4.B.5.A.6.D.7.108°.8.150.9.53°.10.A.
11.D.12.B.13.B.14.③⑤15.40.16.100.
17.【解答】解:∵∠COE是直角,
∴∠COE=90°,
∵∠COF=34°,
∴∠EOF=56°,
∵OF平分∠AOE,
∴∠AOF=∠EOF=56°,
∴∠AOC=56°﹣34°=22°,
∴∠AOD=180°﹣22°=158°.
18.【解答】解:(1)∵∠AOE+∠AOF=180°,∠AOE=40°,
∴∠AOF=180°﹣∠AOE=140°
∵OC平分∠AOF,
∴∠AOC∠AOF140°=70°
∵∠AOB=90°
∴∠BOD=180°﹣∠AOC﹣∠AOB=180°﹣70°﹣90°=20°
(2)方法同(1)可得,若∠AOE=30°,则∠BOD=15°
(3)猜想:∠BOD∠AOE,
理由如下:
∵OC平分∠AOF
∴∠AOC∠AOF
∵∠AOE+∠AOF=180°,
∴∠AOF=180°﹣∠AOE
∵∠BOD+∠AOB+∠AOC=180°,∠AOB=90°
∴∠BOD+90°∠AOF=180°,
∴∠BOD=90°∠AOF=90°﹣90°∠AOE∠AOE.
19.【解答】解:∵∠EOC=90°,
∠COF=34°(已知),
∴∠EOF=56°,
∵OF是∠AOE的角平分线,
∴∠AOF=∠EOF=56°(角平分线的定义),
∴∠AOC=22°,
∵∠AOC+∠EOB=90°,
∠BOO+∠EOB=90°,
∴∠BOD=∠AOC=22°(同角的余角相等),
故答案为:已知;56;∠EOF;角平分线的定义;22;∠EOB;同角的余角相等.
20.【解答】解:(1)∵∠DOE+∠EOF+∠AOF=∠AOD=150°且∠EOF=30°,
∴∠DOE+∠AOF=∠150°﹣30°=120°;
(2)根据补角的定义可知图中与∠BOC互补的角有∠BOD、∠AOC、∠EOF;
(3)∠AOF=∠EOF,理由如下:
∵OM平分∠AOD,
∴∠DOM=∠AOM,
∴∠AOF=∠AOM﹣∠FOM
=∠DOM﹣∠FOM
=∠EOD﹣∠MOE﹣∠FOM
=2∠FOM﹣∠MOE﹣∠FOM
=∠FOM﹣∠MOE
=∠EOF,
∴∠AOF=∠EOF.
第1课时 相交线
1.如图,直线m和n相交于点O,若∠1=40°,则∠2的度数是( )
A.40° B.50° C.140° D.150°
如图所示中,∠1与∠2是邻补角的是( )
A B C D
3.若∠1=64°,则∠1的邻补角度数为 .
4.在下面四个图形中,∠1与∠2是对顶角的是( )
A B C D
5.如图,AB和CD相交于点O,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠1=∠5
6.如图,直线AB、CD相交于点O,OE平分∠AOC,若∠BOD=70°,则∠COE的度数是( )
A.70° B.50° C.40° D.35°
7.如图,直线a、b相交,∠1=36°,则∠2﹣∠3= .
8.如图是一把剪刀,若∠AOB+∠COD=60°,则∠BOD= °.
9.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE= 度.
10.有以下5个说法:①两点之间,线段最短:②相等的角是对顶角:③互补的两个角中必定一个是锐角一个钝角;④两个锐角的和一定是锐角:⑤同角或等角的余角相等.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
11.如图,直线AB、CD相交于点O,∠BOE=90°,OF平分∠AOE,∠1=15°30′,则下列结论不正确的是( )
A.∠2=45° B.∠1=∠3
C.∠AOD+∠1=180° D.∠EOD=75°30'
12.在一个三角形中,一个外角是其相邻内角的2倍,那么这个外角是( )
A.150 B.120° C.100° D.90°
13.如图,直线AB、CD相交于点O,下列描述:
①∠1和∠2互为对顶角;②∠1和∠2互为邻补角;③∠1=∠2;④∠1=∠3
其中正确的是( )
A.①③ B.②④ C.②③ D.①④
14.如图,直线AB和直线CD相交于点O,∠BOE=90°,有下列结论:①∠AOC与∠COE互为余角;②∠AOC=∠BOD;③∠AOC=∠COE;④∠COE与∠DOE互为补角;⑤∠AOC与∠DOE互为补角;⑥∠BOD与∠COE互为余角.其中错误的有 .(填序号)
15.如图,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,那么这个破损扇形零件的圆心角的度数是 °.
16.如图,已知直线AB,CD相交于点O,如果∠BOD=40°,OA平分∠COE,那么∠DOE= 度.
17.如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE,∠COF=34°.求∠AOD的度数.
18.如图,直线EF、CD相交于点O,∠AOB=90°,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)、(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
19.如图,直线AB、CD相交于O,∠EOC=90°,OF是∠AOE的角平分线,∠COF=34°,求∠BOD的度数.
其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
解:∵∠EOC=90°
∠COF=34°( )
∴∠EOF= °
∵OF是∠AOE的角平分线
∴∠AOF= =56°( )
∴∠AOC= °
∵∠AOC+ =90°
∠BOO+∠EOB=90°
∴∠BOD=∠AOC= °( )
20.直线AB、CD相交于点O,∠EOF在∠AOD的内部.
(1)如图①,当∠AOD=150°,∠EOF=30°时,求∠AOF与∠EOD的度数和;
(2)在(1)的条件下,请直接写出图中与∠BOC互补的角;
(3)如图②,若射线OM平分∠AOD(OM在∠EOD内部),且满足∠EOD=2∠FOM,请判断∠AOF与∠EOF的大小关系并说明理由.
参考答案
1.C.2.D.3.116°.4.B.5.A.6.D.7.108°.8.150.9.53°.10.A.
11.D.12.B.13.B.14.③⑤15.40.16.100.
17.【解答】解:∵∠COE是直角,
∴∠COE=90°,
∵∠COF=34°,
∴∠EOF=56°,
∵OF平分∠AOE,
∴∠AOF=∠EOF=56°,
∴∠AOC=56°﹣34°=22°,
∴∠AOD=180°﹣22°=158°.
18.【解答】解:(1)∵∠AOE+∠AOF=180°,∠AOE=40°,
∴∠AOF=180°﹣∠AOE=140°
∵OC平分∠AOF,
∴∠AOC∠AOF140°=70°
∵∠AOB=90°
∴∠BOD=180°﹣∠AOC﹣∠AOB=180°﹣70°﹣90°=20°
(2)方法同(1)可得,若∠AOE=30°,则∠BOD=15°
(3)猜想:∠BOD∠AOE,
理由如下:
∵OC平分∠AOF
∴∠AOC∠AOF
∵∠AOE+∠AOF=180°,
∴∠AOF=180°﹣∠AOE
∵∠BOD+∠AOB+∠AOC=180°,∠AOB=90°
∴∠BOD+90°∠AOF=180°,
∴∠BOD=90°∠AOF=90°﹣90°∠AOE∠AOE.
19.【解答】解:∵∠EOC=90°,
∠COF=34°(已知),
∴∠EOF=56°,
∵OF是∠AOE的角平分线,
∴∠AOF=∠EOF=56°(角平分线的定义),
∴∠AOC=22°,
∵∠AOC+∠EOB=90°,
∠BOO+∠EOB=90°,
∴∠BOD=∠AOC=22°(同角的余角相等),
故答案为:已知;56;∠EOF;角平分线的定义;22;∠EOB;同角的余角相等.
20.【解答】解:(1)∵∠DOE+∠EOF+∠AOF=∠AOD=150°且∠EOF=30°,
∴∠DOE+∠AOF=∠150°﹣30°=120°;
(2)根据补角的定义可知图中与∠BOC互补的角有∠BOD、∠AOC、∠EOF;
(3)∠AOF=∠EOF,理由如下:
∵OM平分∠AOD,
∴∠DOM=∠AOM,
∴∠AOF=∠AOM﹣∠FOM
=∠DOM﹣∠FOM
=∠EOD﹣∠MOE﹣∠FOM
=2∠FOM﹣∠MOE﹣∠FOM
=∠FOM﹣∠MOE
=∠EOF,
∴∠AOF=∠EOF.
