2021-2022学年七年级数学人教版下册5.1.1 相交线练习(word版、含解析)
文档属性
| 名称 | 2021-2022学年七年级数学人教版下册5.1.1 相交线练习(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 121.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 15:33:51 | ||
图片预览




文档简介
人教版七年级下册数学 第五章 相交线与平行线 5.1.1 相交线 习题练习(附答案)
一、单选题(共7题)
1、如图,内错角共有( )
A. 4对 B. 6对 C. 8对 D. 10对
2、下列关于邻补角的说法正确的是( )
A. 有公共顶点,且互补的两个角
B. 和为180°的两个角
C. 有公共顶点,且有一条公共边,另一条边互为反向延长线的两个角
D. 有一条公共边,且相等的两个角
3、下列说法正确的是( )
A. 对顶角不一定相等
B. 有公共顶点,且相等的两个角是对顶角
C. 对顶角的补角相等
D. 两条直线相交所成的角是对顶角
4、下列图形中,∠1与∠2是对顶角的是( )
A. (A) B. (B) C. (C) D. (D)
5、平面内两两相交的8条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A. 16 B. 18 C. 29 D. 28
6、下列说法正确的是( )
A. 不相交的两条直线互相平行
B. 垂直于同一条直线的两条直线互相平行
C. 经过直线外一点有且只有一条直线与这条直线平行
D. 同一平面内,两条直线的位置关系有三种:平行、垂直和相交
7、同一平面内的三条直线最多可把平面分成( )部分
A. 4 B. 5 C. 6 D. 7
二、填空题(共6题)
8、如图,∠AOC和∠BOC互为邻补角,OD,OE分别是∠AOC,∠BOC的平分线,则∠DOE= .
9、如图,直线AB,CD,EF都经过点O,则∠1+∠2+∠3= .
10、观察下列图形,寻找对顶角(不含平角).
(1)如图①,两条直线相交,共有 对对顶角;
(2)如图②,三条直线相交于一点,共有 对对顶角;
(3)如图③,四条直线相交于一点,共有 对对顶角;
……
(4)若n条直线相交于一点,则共有 对对顶角.
11、如图,直线a,b相交,∠1=60°,则∠2= ,∠3= ,∠4= .
12、在平面内,若两条直线的最多交点数记为a1,三条直线的最多交点数记为a2,四条直线的最多交点数记为a3,…,依此类推,则= .
13、如图,当剪子口∠AOB增大15°时,∠COD增大 度.
三、解答题(共4题)
14、如图,P是直线AB上一点,∠APC= ∠BPC,∠CPD=2∠APC.
(1)求∠CPD的度数;
(2)判断PD与AB的位置关系,并说明理由.
15、如图,AB是一条河流,要铺设管道将河水引到C,D两个用水点,现有两种铺设管道的方案.
方案一:分别过点C,D作AB的垂线,垂足分别为点E,F,沿CE,DF铺设管道;
方案二:连接CD交AB于点P,沿PC,PD铺设管道.
这两种铺设管道的方案哪一种更节省材料 为什么
16、如图,直线AB,CD被EF所截,如果∠1与∠2互补,且∠1=110°,那么∠3,∠4的度数分别是多少
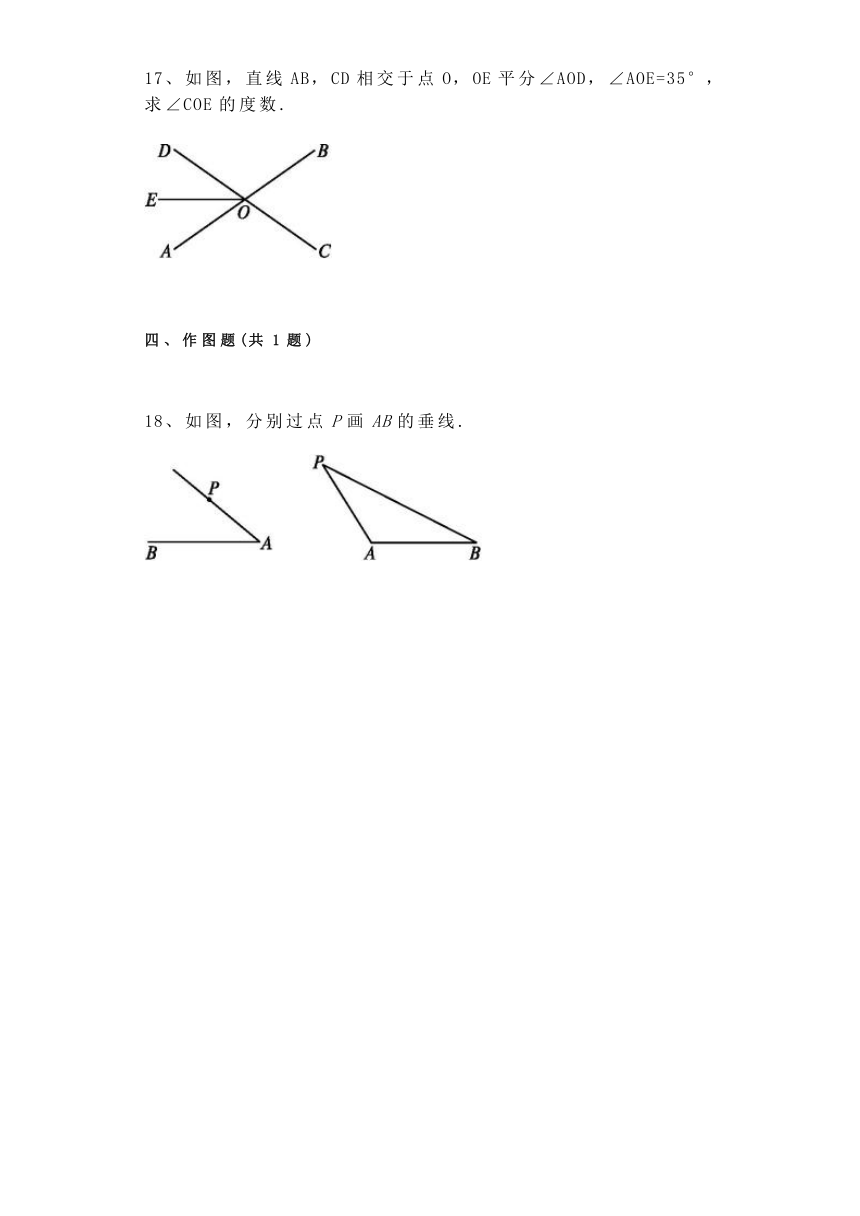
17、如图,直线AB,CD相交于点O,OE平分∠AOD,∠AOE=35°,求∠COE的度数.
四、作图题(共1题)
18、如图,分别过点P画AB的垂线.
试卷答案
1、B
直线AB,DC被直线AD所截,内错角有∠1与∠2,∠3与∠4;直线AB,DC被直线BC所截,内错角有∠8与∠9;直线AD,BC分别被直线AB,CD所截,内错角有∠9与∠10,∠2与∠7,∠5与∠6.所以内错角共有6对.
2、C
3、C
4、C
由对顶角的定义:“有公共顶点,且两边分别互为反向延长线的两个角互为对顶角”分析可知,A、B、D三幅图中的∠1、∠2都不是对顶角,只有C图中的∠1、∠2是对顶角.
故选C.
5、C
试题解析:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,
∵任意三条直线不过同一点,
∴此时交点为:8×(8﹣1)÷2=28,即n=28;
则
故选C.
6、C
分析:正确解答此题的关键是熟练掌握定理的前提条件.
详解:A.不相交的两条直线互相平行,错误,应为:同一平面内:不相交的两条直线互相平行.
B.垂直于同一条直线的两条直线互相平行,错误.应为:同一平面内:垂直于同一条直线的两条直线互相平行.
C. 经过直线外一点有且只有一条直线与这条直线平行,正确.
D.同一平面内,两条直线的位置关系有三种:平行、垂直和相交,错误,应为:同一平面内,两条直线的位置关系有两种:平行、相交.
故选:C.
点睛:本题考查了同一平面内,两条直线间的位置关系.
7、D
如图,三条直线两两相交时将平面分为7部分.
故选D.
8、
90°
由∠AOC和∠BOC互为邻补角可得∠AOC+∠BOC=180°.
由OD,OE分别为∠AOC,∠BOC的平分线可得∠COD= ∠AOC,∠COE= ∠COB.
因为∠DOE=∠COD+∠COE,
所以∠DOE=90°.
9、
180°
∠1+∠2+∠3=∠1+∠AOD+∠3=180°.
10、
(1)2 (2)6 (3)12 (4)n(n-1)
数对顶角的对数时,要按照一定的规律数,以保证“不重不漏”.探索n条直线时,列下表来寻找规律.
直线的条数 2 3 4 … n
对顶角的对数 2 6 12 … n(n-1)
11、 (1). 120°; (2). 60°; (3). 120°
试题解析:∵直线a,b相交,
∵∠1与∠3是对顶角,∠2与∠4是对顶角,
故答案为:
12、
如图:2条直线相交有1个交点;
3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;…
n条直线相交有
.
则
.
故答案是: .
点睛:画出图形,根据具体图形求出两条直线相交、三条直线相交、四条直线相交时的交点个数,总结出规律,即可计算出2013条直线相交时的交点个数.此题在相交线的基础上,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊项一般猜想的方法.
13、15
当剪子口∠AOB增大25 时,∠COD增大25度,
故答案为:25.
14、
解 :(1)因为平角∠APB=180°,∠APC= ∠BPC,
所以∠APC=180°÷6=30°.
所以∠CPD=2∠APC=60°.
(2)PD⊥AB.
理由:∠APD=∠APC+∠CPD=30°+60°=90°,即∠APD是直角,因此PD⊥AB.
15、
解 :按方案一铺设管道更节省材料.
理由如下:
因为CE⊥AB,DF⊥AB,而AB与CD不垂直,
由“垂线段最短”的性质,
可知CE则CE+DF故沿CE,DF铺设管道更节省材料.
16、
解 因为∠1与∠2互补,∠1=110°,
所以∠2=180°-110°=70°.
因为∠2与∠3是对顶角,
所以∠3=∠2=70°.
又因为∠1+∠4=180°,
所以∠4=180°-∠1=180°-110°=70°.
17、
解 因为OE平分∠AOD,∠AOE=35°,
所以∠AOD=2∠AOE=70°.
由∠AOD与∠AOC是邻补角,得∠AOC=180°-∠AOD=110°,
因此∠COE=∠AOE+∠AOC=35°+110°=145°.
18、
解 如图.
由点到直线的距离的定义可解(1).对于(3),AC,CD都是点C与直线AD上的点的连线,根据“垂线段最短”可比较两者的长短.
一、单选题(共7题)
1、如图,内错角共有( )
A. 4对 B. 6对 C. 8对 D. 10对
2、下列关于邻补角的说法正确的是( )
A. 有公共顶点,且互补的两个角
B. 和为180°的两个角
C. 有公共顶点,且有一条公共边,另一条边互为反向延长线的两个角
D. 有一条公共边,且相等的两个角
3、下列说法正确的是( )
A. 对顶角不一定相等
B. 有公共顶点,且相等的两个角是对顶角
C. 对顶角的补角相等
D. 两条直线相交所成的角是对顶角
4、下列图形中,∠1与∠2是对顶角的是( )
A. (A) B. (B) C. (C) D. (D)
5、平面内两两相交的8条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A. 16 B. 18 C. 29 D. 28
6、下列说法正确的是( )
A. 不相交的两条直线互相平行
B. 垂直于同一条直线的两条直线互相平行
C. 经过直线外一点有且只有一条直线与这条直线平行
D. 同一平面内,两条直线的位置关系有三种:平行、垂直和相交
7、同一平面内的三条直线最多可把平面分成( )部分
A. 4 B. 5 C. 6 D. 7
二、填空题(共6题)
8、如图,∠AOC和∠BOC互为邻补角,OD,OE分别是∠AOC,∠BOC的平分线,则∠DOE= .
9、如图,直线AB,CD,EF都经过点O,则∠1+∠2+∠3= .
10、观察下列图形,寻找对顶角(不含平角).
(1)如图①,两条直线相交,共有 对对顶角;
(2)如图②,三条直线相交于一点,共有 对对顶角;
(3)如图③,四条直线相交于一点,共有 对对顶角;
……
(4)若n条直线相交于一点,则共有 对对顶角.
11、如图,直线a,b相交,∠1=60°,则∠2= ,∠3= ,∠4= .
12、在平面内,若两条直线的最多交点数记为a1,三条直线的最多交点数记为a2,四条直线的最多交点数记为a3,…,依此类推,则= .
13、如图,当剪子口∠AOB增大15°时,∠COD增大 度.
三、解答题(共4题)
14、如图,P是直线AB上一点,∠APC= ∠BPC,∠CPD=2∠APC.
(1)求∠CPD的度数;
(2)判断PD与AB的位置关系,并说明理由.
15、如图,AB是一条河流,要铺设管道将河水引到C,D两个用水点,现有两种铺设管道的方案.
方案一:分别过点C,D作AB的垂线,垂足分别为点E,F,沿CE,DF铺设管道;
方案二:连接CD交AB于点P,沿PC,PD铺设管道.
这两种铺设管道的方案哪一种更节省材料 为什么
16、如图,直线AB,CD被EF所截,如果∠1与∠2互补,且∠1=110°,那么∠3,∠4的度数分别是多少
17、如图,直线AB,CD相交于点O,OE平分∠AOD,∠AOE=35°,求∠COE的度数.
四、作图题(共1题)
18、如图,分别过点P画AB的垂线.
试卷答案
1、B
直线AB,DC被直线AD所截,内错角有∠1与∠2,∠3与∠4;直线AB,DC被直线BC所截,内错角有∠8与∠9;直线AD,BC分别被直线AB,CD所截,内错角有∠9与∠10,∠2与∠7,∠5与∠6.所以内错角共有6对.
2、C
3、C
4、C
由对顶角的定义:“有公共顶点,且两边分别互为反向延长线的两个角互为对顶角”分析可知,A、B、D三幅图中的∠1、∠2都不是对顶角,只有C图中的∠1、∠2是对顶角.
故选C.
5、C
试题解析:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,
∵任意三条直线不过同一点,
∴此时交点为:8×(8﹣1)÷2=28,即n=28;
则
故选C.
6、C
分析:正确解答此题的关键是熟练掌握定理的前提条件.
详解:A.不相交的两条直线互相平行,错误,应为:同一平面内:不相交的两条直线互相平行.
B.垂直于同一条直线的两条直线互相平行,错误.应为:同一平面内:垂直于同一条直线的两条直线互相平行.
C. 经过直线外一点有且只有一条直线与这条直线平行,正确.
D.同一平面内,两条直线的位置关系有三种:平行、垂直和相交,错误,应为:同一平面内,两条直线的位置关系有两种:平行、相交.
故选:C.
点睛:本题考查了同一平面内,两条直线间的位置关系.
7、D
如图,三条直线两两相交时将平面分为7部分.
故选D.
8、
90°
由∠AOC和∠BOC互为邻补角可得∠AOC+∠BOC=180°.
由OD,OE分别为∠AOC,∠BOC的平分线可得∠COD= ∠AOC,∠COE= ∠COB.
因为∠DOE=∠COD+∠COE,
所以∠DOE=90°.
9、
180°
∠1+∠2+∠3=∠1+∠AOD+∠3=180°.
10、
(1)2 (2)6 (3)12 (4)n(n-1)
数对顶角的对数时,要按照一定的规律数,以保证“不重不漏”.探索n条直线时,列下表来寻找规律.
直线的条数 2 3 4 … n
对顶角的对数 2 6 12 … n(n-1)
11、 (1). 120°; (2). 60°; (3). 120°
试题解析:∵直线a,b相交,
∵∠1与∠3是对顶角,∠2与∠4是对顶角,
故答案为:
12、
如图:2条直线相交有1个交点;
3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;…
n条直线相交有
.
则
.
故答案是: .
点睛:画出图形,根据具体图形求出两条直线相交、三条直线相交、四条直线相交时的交点个数,总结出规律,即可计算出2013条直线相交时的交点个数.此题在相交线的基础上,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊项一般猜想的方法.
13、15
当剪子口∠AOB增大25 时,∠COD增大25度,
故答案为:25.
14、
解 :(1)因为平角∠APB=180°,∠APC= ∠BPC,
所以∠APC=180°÷6=30°.
所以∠CPD=2∠APC=60°.
(2)PD⊥AB.
理由:∠APD=∠APC+∠CPD=30°+60°=90°,即∠APD是直角,因此PD⊥AB.
15、
解 :按方案一铺设管道更节省材料.
理由如下:
因为CE⊥AB,DF⊥AB,而AB与CD不垂直,
由“垂线段最短”的性质,
可知CE
16、
解 因为∠1与∠2互补,∠1=110°,
所以∠2=180°-110°=70°.
因为∠2与∠3是对顶角,
所以∠3=∠2=70°.
又因为∠1+∠4=180°,
所以∠4=180°-∠1=180°-110°=70°.
17、
解 因为OE平分∠AOD,∠AOE=35°,
所以∠AOD=2∠AOE=70°.
由∠AOD与∠AOC是邻补角,得∠AOC=180°-∠AOD=110°,
因此∠COE=∠AOE+∠AOC=35°+110°=145°.
18、
解 如图.
由点到直线的距离的定义可解(1).对于(3),AC,CD都是点C与直线AD上的点的连线,根据“垂线段最短”可比较两者的长短.
