2021-2022学年七年级数学人教版下册5.3.1平行线的性质教案
文档属性
| 名称 | 2021-2022学年七年级数学人教版下册5.3.1平行线的性质教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 375.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览



文档简介
5.3.1 平行线的性质
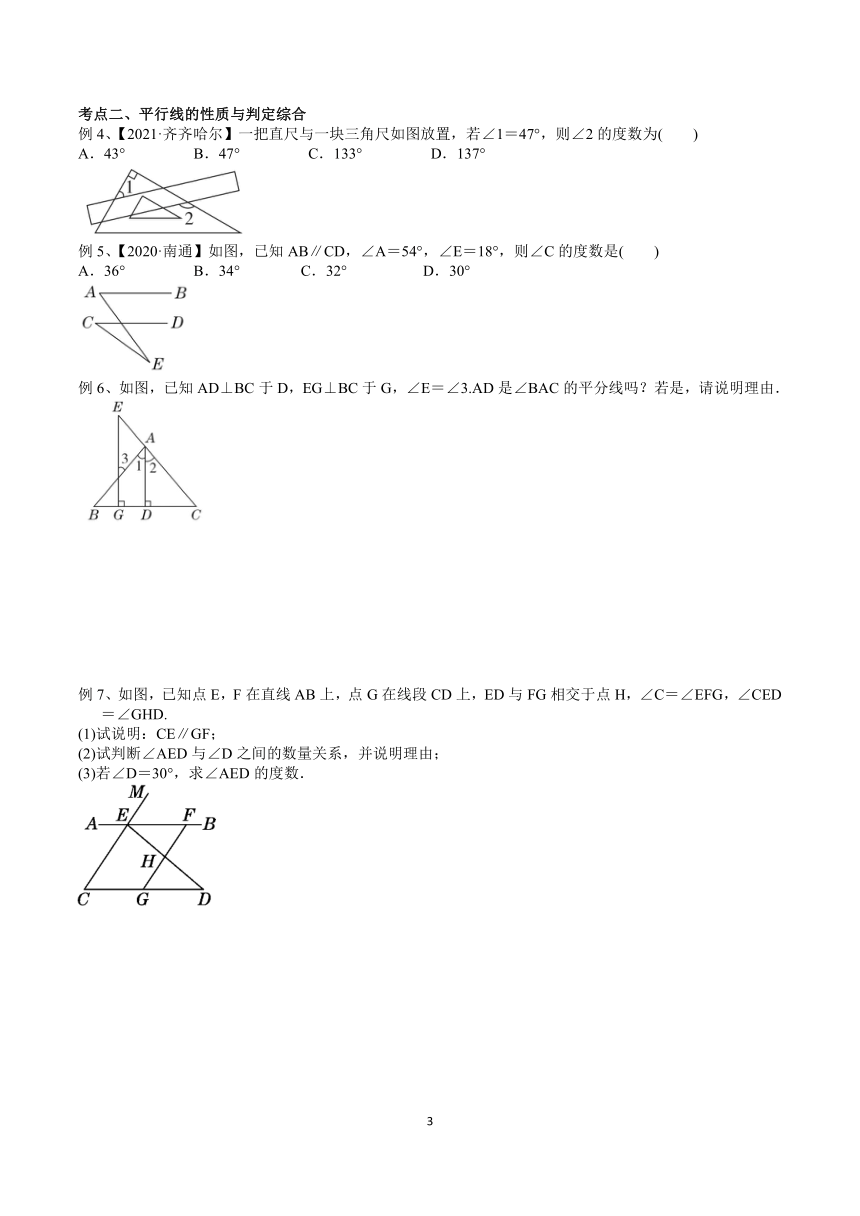
知识点一、平行线的性质
判定方法 文字语言 图示 符号语言
判定方法1:两直线平行,同位角相等; 两条平行线被第三条直线所截,同位角相等 ∵AB//CD ∴∠3=∠7
判定方法2:两直线平行,内错角相等; 两条平行线被第三条直线所截,内错角相等 ∵AB//CD ∴∠1=∠7
判定方法3:两直线平行,同旁内角互补; 两条平行线被第三条直线所截,同旁内角互补 ∵AB//CD ∴∠1+∠6=180°
温馨提示:只有在两条直线平行的前提下,才有同位角相等,内错角相等,同旁内角互补。
考点一、平行线的性质
例1、【2021·遵义】如图,已知直线a∥b,c为截线,若∠1=60°,则∠2的度数是( )
A.30° B.60° C.120° D.150°
例2、【2021·大连】如图,AB∥CD,CE⊥AD,垂足为E,若∠A=40°,则∠C的度数为( )
A.40° B.50° C.60° D.90°
例3、【中考·重庆】如图,AB∥CD,三角形EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD.若∠EFG=90°,∠E=35°,求∠EFB的度数.
变式1、【2021·河南】如图,a∥b,∠1=60°,则∠2的度数为( )
A.90° B.100° C.110° D.120°
变式2、【2021·长沙】如图,AB∥CD,EF分别与AB,CD交于点G,H,∠AGE=100°,则∠DHF的度数为( )
A.100° B.80° C.50° D.40°
变式3、【2021·呼和浩特】如图,在三角形ABC中,∠B=50°,∠C=70°,直线DE经过点A,∠DAB=50°,则∠EAC的度数是( )
A.40° B .50° C.60° D.70°
变式4、【2021·包头】如图,直线l1∥l2,直线l3交l1于点A,交l2于点B,过点B的直线l4交l1于点C.若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
A.80° B.70° C.60° D.50°
变式5、【2021·济宁】如图,AB∥CD,BC∥DE,若∠B=72°28′,那么∠D的度数是( )
A.72°28′ B.101°28′ C.107°32′ D.127°32′
变式6、已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( )
A.50° B.130° C.50°或130° D.不能确定
变式7、如图,点C在直线GF上,AB∥DE∥GF,∠1:∠D:∠B=2:3:4.求∠1的度数.
考点二、平行线的性质与判定综合
例4、【2021·齐齐哈尔】一把直尺与一块三角尺如图放置,若∠1=47°,则∠2的度数为( )
A.43° B.47° C.133° D.137°
例5、【2020·南通】如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A.36° B.34° C.32° D.30°
例6、如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠3.AD是∠BAC的平分线吗?若是,请说明理由.
例7、如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG相交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试说明:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠D=30°,求∠AED的度数.
变式1、【2021·聊城】如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,则∠CEF的度数为( )
A.95° B.105° C.110° D.115°
变式2、【2021·娄底】如图,AB∥CD,点E,F在AC上,已知∠CED=70°,∠BFC=130°,则∠B+∠D的度数为( )
A.40° B.50° C.60° D.70°
变式3、如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠2=∠4
变式4、【2021·东营】如图,AB∥CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE=( )
A.30° B.40° C.50° D.60°
变式5、【2021·荆州】阅读下列材料,①~④步中数学依据错误的是( )
A . ① B.② C.③ D.④
变式7、【2021·武汉】如图,直线EF分别与直线AB,CD相交于点E,F.EM平分∠BEF,FN平分∠CFE,且EM∥FN.试说明AB∥CD.
变式8、如图,已知∠1=∠2,∠BAC=20°,∠ACF=80°.
(1)求∠2的度数.
(2)FC与AD平行吗?为什么?
(3)根据以上结论,你能确定∠ADB与∠FCB的大小关系吗?请说明理由.
1、【2021·云南】如图,直线c与直线a,b都相交.若a∥b,∠1=55°,则∠2=( )
A.60° B.55° C.50° D.45°
2、【2021·新疆】如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
3、【2021·眉山】如图,将直角三角尺放置在长方形纸片上,若∠1=48°,则∠2的度数为( )
A.42° B.48° C.52° D.60°
4、如图,已知直线a∥b,直线c与直线a,b分别交于点A,B.若∠1=54°,则∠2等于( )
A.126° B.134°
C.136° D.144°
5、【2021·岳阳】将一副直角三角尺按如图方式摆放,若直线a∥b,则∠1的大小为( )
A.45° B.60° C.75° D.105°
6、【2021·白银】如图,直线DE∥BF,直角三角形ABC的直角顶点B在BF上,若∠CBF=20°,则∠ADE=( )
A.70° B.60° C.75° D.80°
7、【2021·宜昌】如图,将一副三角尺按图中所示位置摆放,点F在AC上,其中∠ACB=90°,∠ABC=60°,∠EFD=90°,∠DEF=45°,AB∥DE,则∠AFD的度数是( )
A.15° B.30° C.45° D.60°
8、如图,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.
其中正确的有( )
A.①②④ B.②③④
C.③④ D.①②③④
9、【2021·恩施州】如图,已知AE∥BC,∠BAC=100°,∠DAE=50°,则∠C=____.
10、如图,AC∥DF,AB∥EF,点D,E分别在AB,AC上.若∠2=50°,求∠1的度数.
11、已知:如图,在四边形ABCD中,AD∥BC,AB∥DC,试说明:∠B=∠D.
12、【中考·重庆】如图,直线EF∥GH,点A在EF上,AC交GH于点B.若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
13、把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′,C′的位置上,ED′与BC的交点为G,如图所示.若∠EFG=60°,求∠1与∠2的度数.
14、【2021·武汉】如图,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F,试说明:∠DEF=∠F.
15、如图,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°.求∠BPC的度数.
16、如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断BC与DE的位置关系,并说明理由;
(2)若∠A=35°,求∠F的度数.
17、【探索】小明和小亮在研究一个数学问题:
已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
【发现】在图①中,小明和小亮都发现∠APC=∠A+∠C.
小明是这样解答的:过点P在∠APC的内部作PQ∥AB,
∴∠APQ=∠A(_______________________).
∵PQ∥AB,AB∥CD,
∴PQ∥CD(________________________________).
∴∠CPQ=∠C.
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
小亮是这样解答的:过点P作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C.
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
请在上面解答过程中的横线上填写依据.
两人的解答过程中,完全正确的是________.
【应用】在图②中,若∠A=120°,∠C=140°,则∠P的度数为________;
在图③中,若∠A=30°,∠C=70°,则∠P的度数为________.
【拓展】在图④中,探索∠P与∠A,∠C的数量关系,并说明理由.
知识点一、平行线的性质
判定方法 文字语言 图示 符号语言
判定方法1:两直线平行,同位角相等; 两条平行线被第三条直线所截,同位角相等 ∵AB//CD ∴∠3=∠7
判定方法2:两直线平行,内错角相等; 两条平行线被第三条直线所截,内错角相等 ∵AB//CD ∴∠1=∠7
判定方法3:两直线平行,同旁内角互补; 两条平行线被第三条直线所截,同旁内角互补 ∵AB//CD ∴∠1+∠6=180°
温馨提示:只有在两条直线平行的前提下,才有同位角相等,内错角相等,同旁内角互补。
考点一、平行线的性质
例1、【2021·遵义】如图,已知直线a∥b,c为截线,若∠1=60°,则∠2的度数是( )
A.30° B.60° C.120° D.150°
例2、【2021·大连】如图,AB∥CD,CE⊥AD,垂足为E,若∠A=40°,则∠C的度数为( )
A.40° B.50° C.60° D.90°
例3、【中考·重庆】如图,AB∥CD,三角形EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD.若∠EFG=90°,∠E=35°,求∠EFB的度数.
变式1、【2021·河南】如图,a∥b,∠1=60°,则∠2的度数为( )
A.90° B.100° C.110° D.120°
变式2、【2021·长沙】如图,AB∥CD,EF分别与AB,CD交于点G,H,∠AGE=100°,则∠DHF的度数为( )
A.100° B.80° C.50° D.40°
变式3、【2021·呼和浩特】如图,在三角形ABC中,∠B=50°,∠C=70°,直线DE经过点A,∠DAB=50°,则∠EAC的度数是( )
A.40° B .50° C.60° D.70°
变式4、【2021·包头】如图,直线l1∥l2,直线l3交l1于点A,交l2于点B,过点B的直线l4交l1于点C.若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
A.80° B.70° C.60° D.50°
变式5、【2021·济宁】如图,AB∥CD,BC∥DE,若∠B=72°28′,那么∠D的度数是( )
A.72°28′ B.101°28′ C.107°32′ D.127°32′
变式6、已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( )
A.50° B.130° C.50°或130° D.不能确定
变式7、如图,点C在直线GF上,AB∥DE∥GF,∠1:∠D:∠B=2:3:4.求∠1的度数.
考点二、平行线的性质与判定综合
例4、【2021·齐齐哈尔】一把直尺与一块三角尺如图放置,若∠1=47°,则∠2的度数为( )
A.43° B.47° C.133° D.137°
例5、【2020·南通】如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A.36° B.34° C.32° D.30°
例6、如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠3.AD是∠BAC的平分线吗?若是,请说明理由.
例7、如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG相交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试说明:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠D=30°,求∠AED的度数.
变式1、【2021·聊城】如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,则∠CEF的度数为( )
A.95° B.105° C.110° D.115°
变式2、【2021·娄底】如图,AB∥CD,点E,F在AC上,已知∠CED=70°,∠BFC=130°,则∠B+∠D的度数为( )
A.40° B.50° C.60° D.70°
变式3、如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠2=∠4
变式4、【2021·东营】如图,AB∥CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE=( )
A.30° B.40° C.50° D.60°
变式5、【2021·荆州】阅读下列材料,①~④步中数学依据错误的是( )
A . ① B.② C.③ D.④
变式7、【2021·武汉】如图,直线EF分别与直线AB,CD相交于点E,F.EM平分∠BEF,FN平分∠CFE,且EM∥FN.试说明AB∥CD.
变式8、如图,已知∠1=∠2,∠BAC=20°,∠ACF=80°.
(1)求∠2的度数.
(2)FC与AD平行吗?为什么?
(3)根据以上结论,你能确定∠ADB与∠FCB的大小关系吗?请说明理由.
1、【2021·云南】如图,直线c与直线a,b都相交.若a∥b,∠1=55°,则∠2=( )
A.60° B.55° C.50° D.45°
2、【2021·新疆】如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
3、【2021·眉山】如图,将直角三角尺放置在长方形纸片上,若∠1=48°,则∠2的度数为( )
A.42° B.48° C.52° D.60°
4、如图,已知直线a∥b,直线c与直线a,b分别交于点A,B.若∠1=54°,则∠2等于( )
A.126° B.134°
C.136° D.144°
5、【2021·岳阳】将一副直角三角尺按如图方式摆放,若直线a∥b,则∠1的大小为( )
A.45° B.60° C.75° D.105°
6、【2021·白银】如图,直线DE∥BF,直角三角形ABC的直角顶点B在BF上,若∠CBF=20°,则∠ADE=( )
A.70° B.60° C.75° D.80°
7、【2021·宜昌】如图,将一副三角尺按图中所示位置摆放,点F在AC上,其中∠ACB=90°,∠ABC=60°,∠EFD=90°,∠DEF=45°,AB∥DE,则∠AFD的度数是( )
A.15° B.30° C.45° D.60°
8、如图,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.
其中正确的有( )
A.①②④ B.②③④
C.③④ D.①②③④
9、【2021·恩施州】如图,已知AE∥BC,∠BAC=100°,∠DAE=50°,则∠C=____.
10、如图,AC∥DF,AB∥EF,点D,E分别在AB,AC上.若∠2=50°,求∠1的度数.
11、已知:如图,在四边形ABCD中,AD∥BC,AB∥DC,试说明:∠B=∠D.
12、【中考·重庆】如图,直线EF∥GH,点A在EF上,AC交GH于点B.若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
13、把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′,C′的位置上,ED′与BC的交点为G,如图所示.若∠EFG=60°,求∠1与∠2的度数.
14、【2021·武汉】如图,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F,试说明:∠DEF=∠F.
15、如图,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°.求∠BPC的度数.
16、如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断BC与DE的位置关系,并说明理由;
(2)若∠A=35°,求∠F的度数.
17、【探索】小明和小亮在研究一个数学问题:
已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
【发现】在图①中,小明和小亮都发现∠APC=∠A+∠C.
小明是这样解答的:过点P在∠APC的内部作PQ∥AB,
∴∠APQ=∠A(_______________________).
∵PQ∥AB,AB∥CD,
∴PQ∥CD(________________________________).
∴∠CPQ=∠C.
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
小亮是这样解答的:过点P作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C.
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
请在上面解答过程中的横线上填写依据.
两人的解答过程中,完全正确的是________.
【应用】在图②中,若∠A=120°,∠C=140°,则∠P的度数为________;
在图③中,若∠A=30°,∠C=70°,则∠P的度数为________.
【拓展】在图④中,探索∠P与∠A,∠C的数量关系,并说明理由.
