6.2 立方根 课件(23页ppt)
图片预览






文档简介
(共23张PPT)
人教版 七年级下
第六章 实数
精品同步教学课件
6.2 立方根(共2课时)
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础一般的学生使用。课件包括以下环节:
新知引入
典例讲解
新知学习
随堂练习
拓展提高
课堂小结
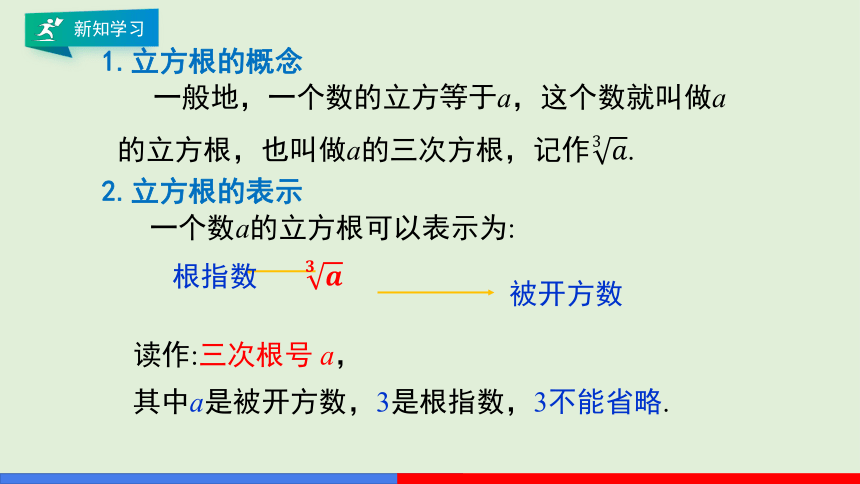
1.立方根的概念
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根,记作.
2.立方根的表示
一个数a的立方根可以表示为:
根指数
被开方数
其中a是被开方数,3是根指数,3不能省略.
读作:三次根号 a,
新知学习
求一个数的立方根的运算叫作开立方.
开立方与立方互为逆运算.
新知学习
填一填 根据立方根的意义填空:
因为=8,所以8的立方根是( );
因为( )3 =0.125,所以0.125的立方是( );
因为( )3 =0,所以0的立方根是( );
因为 ( )3 =-8,所以-8的立方根是( );
因为( )3 = ,所以 的立方根是( ).
0
2
0
3.立方根的性质
思考:立方根是它本身的数有?
新知学习
练一练:判断下列说法是否正确.
x
(2) 25的平方根是5;
x
(3) 没有立方根;
x
x
(5) 0的平方根和立方根都是0.
(1)的立方根是;
(4) 的平方根是
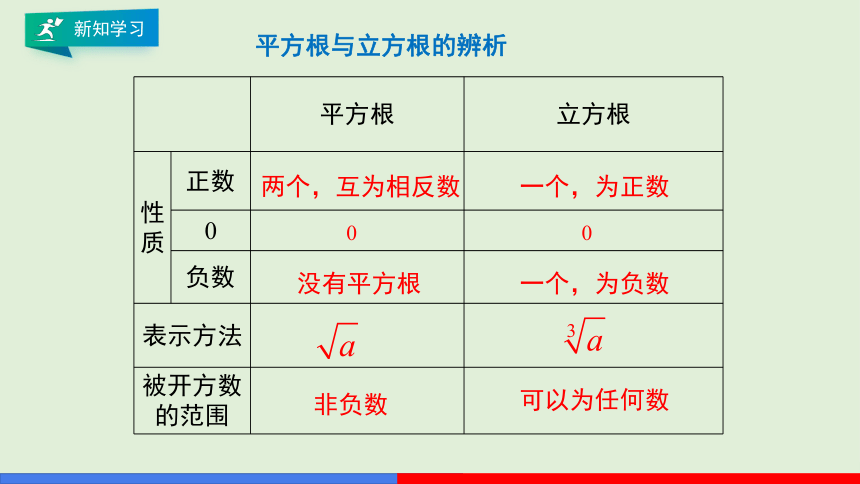
平方根与立方根的辨析
平方根 立方根
性 质 正数
0
负数
表示方法
被开方数的范围
两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
可以为任何数
非负数
新知学习
求下列各数的立方根:
(1); (2);
例1
典例讲解
解:(1)-5
(2)
(3)-
(5) -5的立方根是
(3)
(4)0.216;
(5)-5.
典例讲解
(3)
求下列各数的立方根:
(1)
(2)
(3)
(4)
(5)
典例讲解
所以
因为
=
,
=
所以
因为 = , = ,
互为相反数的数的立方根也互为相反数
你能从上述问题中总结出互为相反数的两个数与的立方根的关系吗
一般地,
=
,
.
.
4.立方根的规律探究一
新知学习
求下列各式的值:
例2
(1); (2) ; (3).
典例讲解
解(1)4(2)-
(3)-
0.5
-3
12
1
c课堂练习
2.求下列各式的值.
(1)
(2)
(3)
(4)
– 0.3
先填写下表,再回答问题
0.000001 0.001 1 1000 1000000
0
从上面问题中你发现什么
小结:被开方数的小数点向左或向右移动3位时,立方根的小数点就相应的向左或向右移动1位.
5.立方根的规律探究二
新知学习
填空
= 6
= 0.6
= 0.06
= 60
课堂练习
例2 计算: .
解:原式=3+2-(-1) =5+1=6.
例1 的算术平方根是 .
2
典例讲解
例3.比较3,4, 的大小.
解:33 = 27,43 = 64
因为27 < 50 < 64
所以3 < < 4
典例讲解
例4 课本P52习题第5题
典例讲解
1.求下列各式的值.
(1)
(2)
(3)
(4)
= – 0.3
=
=
=
=
=
课堂练习
2.比较下列各组数的大小.
(1) 与2; (2) 与 .
解:因为 = 9
23 = 8
所以 > 8
所以 > 2
因为 = 3
所以 3 <
所以 <
课堂练习
https://www.21cnjy.com/help/help_extract.php
人教版 七年级下
第六章 实数
精品同步教学课件
6.2 立方根(共2课时)
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础一般的学生使用。课件包括以下环节:
新知引入
典例讲解
新知学习
随堂练习
拓展提高
课堂小结
1.立方根的概念
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根,记作.
2.立方根的表示
一个数a的立方根可以表示为:
根指数
被开方数
其中a是被开方数,3是根指数,3不能省略.
读作:三次根号 a,
新知学习
求一个数的立方根的运算叫作开立方.
开立方与立方互为逆运算.
新知学习
填一填 根据立方根的意义填空:
因为=8,所以8的立方根是( );
因为( )3 =0.125,所以0.125的立方是( );
因为( )3 =0,所以0的立方根是( );
因为 ( )3 =-8,所以-8的立方根是( );
因为( )3 = ,所以 的立方根是( ).
0
2
0
3.立方根的性质
思考:立方根是它本身的数有?
新知学习
练一练:判断下列说法是否正确.
x
(2) 25的平方根是5;
x
(3) 没有立方根;
x
x
(5) 0的平方根和立方根都是0.
(1)的立方根是;
(4) 的平方根是
平方根与立方根的辨析
平方根 立方根
性 质 正数
0
负数
表示方法
被开方数的范围
两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
可以为任何数
非负数
新知学习
求下列各数的立方根:
(1); (2);
例1
典例讲解
解:(1)-5
(2)
(3)-
(5) -5的立方根是
(3)
(4)0.216;
(5)-5.
典例讲解
(3)
求下列各数的立方根:
(1)
(2)
(3)
(4)
(5)
典例讲解
所以
因为
=
,
=
所以
因为 = , = ,
互为相反数的数的立方根也互为相反数
你能从上述问题中总结出互为相反数的两个数与的立方根的关系吗
一般地,
=
,
.
.
4.立方根的规律探究一
新知学习
求下列各式的值:
例2
(1); (2) ; (3).
典例讲解
解(1)4(2)-
(3)-
0.5
-3
12
1
c课堂练习
2.求下列各式的值.
(1)
(2)
(3)
(4)
– 0.3
先填写下表,再回答问题
0.000001 0.001 1 1000 1000000
0
从上面问题中你发现什么
小结:被开方数的小数点向左或向右移动3位时,立方根的小数点就相应的向左或向右移动1位.
5.立方根的规律探究二
新知学习
填空
= 6
= 0.6
= 0.06
= 60
课堂练习
例2 计算: .
解:原式=3+2-(-1) =5+1=6.
例1 的算术平方根是 .
2
典例讲解
例3.比较3,4, 的大小.
解:33 = 27,43 = 64
因为27 < 50 < 64
所以3 < < 4
典例讲解
例4 课本P52习题第5题
典例讲解
1.求下列各式的值.
(1)
(2)
(3)
(4)
= – 0.3
=
=
=
=
=
课堂练习
2.比较下列各组数的大小.
(1) 与2; (2) 与 .
解:因为 = 9
23 = 8
所以 > 8
所以 > 2
因为 = 3
所以 3 <
所以 <
课堂练习
https://www.21cnjy.com/help/help_extract.php
