人教版数学八上高分笔记之导与练13.4课题学习 最短路径(原卷+答案)
文档属性
| 名称 | 人教版数学八上高分笔记之导与练13.4课题学习 最短路径(原卷+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 07:53:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
13.4 课题学习 最短路径
知识要点:
两点之间的所有连线中, 最短.
2.连接直线外一点与直线上各点的所有线段中, 最短.
易错点睛:
如图,A,B在直线l异侧,在直线l上取一点P,使PA+PB最小.
【点睛】易模仿课本上的解法而出错.
典例讲解:
题型一、线段和的最小值问题
例1、如图,在等边三角形ABC中,E是边AC的中点,AD是边BC上的中线,P是AD上的动点.若AD=5,则EP+CP的最小值为( )
A.2 B.4 C.5 D.7
解题策略:等边三角形、等腰三角形以及正方形是轴对称图形,某些顶点的对称点与该图形上的点是重合的,利用这个性质可以解决线段和的最小值问题.
变式练习:
如图,在ΔABC中,AB=AC,AD,CE是ΔABC的两条中线,P是AD上一动点,则下列线段的长度等于PB+PE的最小值的是( )
BC B.CE C.AD D.AC
2、如图,在RtΔABC中,∠C=90°,∠B=30°,BC=16,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是 ______
题型二、周长最小值问题
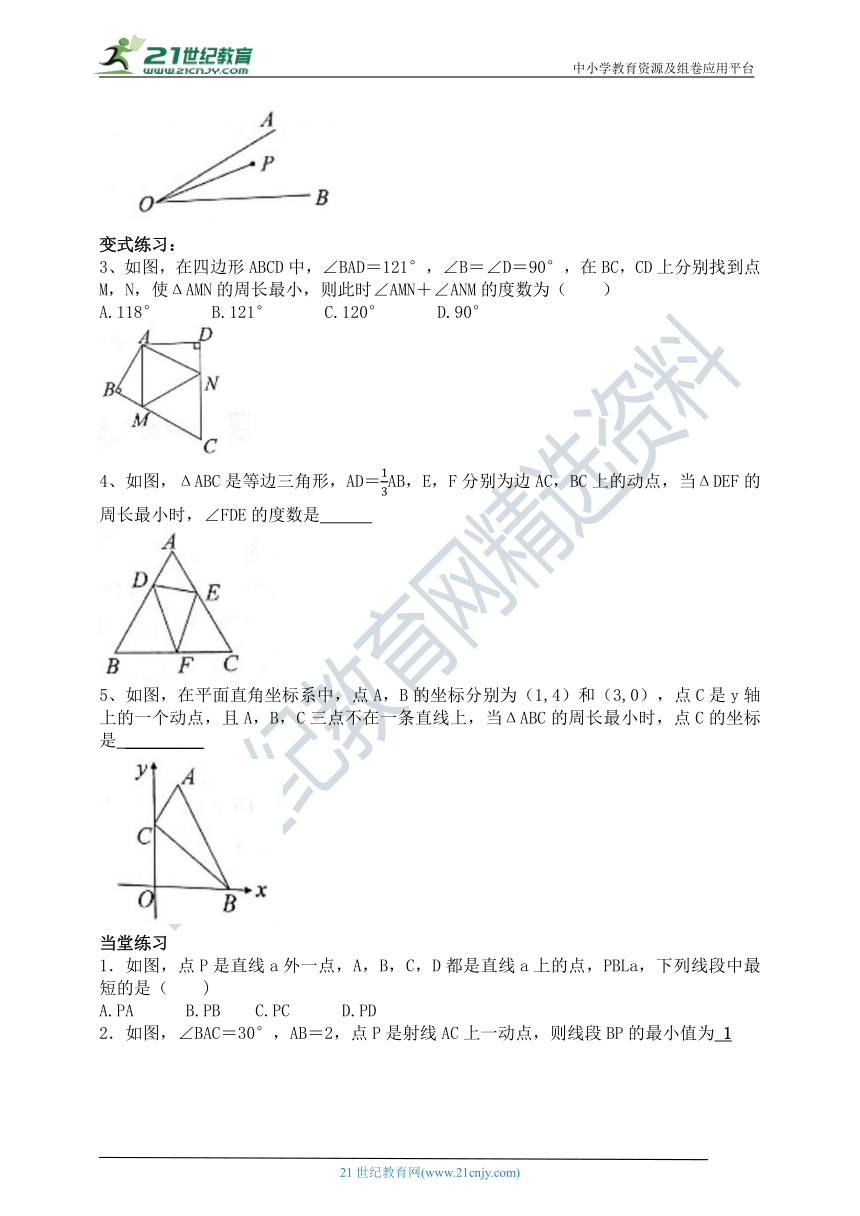
例2、如图,∠AOB=30°,点P为∠AOB内一点,OP=10,点M,N分别在OA,OB上,求ΔPMN周长的最小值.
变式练习:
3、如图,在四边形ABCD中,∠BAD=121°,∠B=∠D=90°,在BC,CD上分别找到点M,N,使ΔAMN的周长最小,则此时∠AMN+∠ANM的度数为( )
A.118° B.121° C.120° D.90°
4、如图,ΔABC是等边三角形,AD=AB,E,F分别为边AC,BC上的动点,当ΔDEF的周长最小时,∠FDE的度数是
5、如图,在平面直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在一条直线上,当ΔABC的周长最小时,点C的坐标是 _________
当堂练习
如图,点P是直线a外一点,A,B,C,D都是直线a上的点,PBLa,下列线段中最短的是( )
A.PA B.PB C.PC D.PD
2.如图,∠BAC=30°,AB=2,点P是射线AC上一动点,则线段BP的最小值为 1
3.如图,在ΔABC中,∠ACB=90°,AC=8,BC=6,AB=10.点E是AB上一动点,则CE的最小值为 ______
4.如图,直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个供水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( )
5.如图,在ΔABC中,ABLAC,AB=3,BC=5,AC=4,EF为BC的垂直平分线,点P为直线EF上的任意一点,则ΔABP周长的最小值是( )
A.12 B.6 C.7 D.8
如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )
A.(-2,0) C.(2,0) B.(4,0) D.(0,0)
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题(用直尺画图).
(1)画出格点ΔABC(顶点均在格点上)关于直线DE对称的ΔA1B1C1;
(2)在DE上画出点P,使PB1+PC最小;
(3)在DE上画出点Q,使QA+QC最小.
如图,要在一条河上架一座桥MN(河的两岸互相平行,桥与河岸垂直),在如下四种方案中,使得E,F两地的路程最短的是( )
9.如图,点A,B在直线l的同侧,在直线l上求作一点P,使|PB-PA|的值最大.
10.如图,点A,B在直线l的两侧,在直线l上求一点作P,使|PA-PB|的值最大.
解:作点A关于直线l的对称点A',连接A'B并延长交直线l于点P.
如图,在RtΔABC中,∠BAC=30°,∠ACB=90°,AC=3,E为AB的中点,在线段AC上找一点H,使得BH+EH的值最小,并求出该最小值.
答案:
知识要点:
两点之间的所有连线中, 线段 最短.
2.连接直线外一点与直线上各点的所有线段中,垂线段 最短.
易错点睛:
如图,A,B在直线l异侧,在直线l上取一点P,使PA+PB最小.
【点睛】易模仿课本上的解法而出错.
【解】 连接AB交直线l于P.运用垂线段最短求最值
典例讲解:
题型一、线段和的最小值问题
例1、如图,在等边三角形ABC中,E是边AC的中点,AD是边BC上的中线,P是AD上的动点.若AD=5,则EP+CP的最小值为( )
A.2 B.4 C.5 D.7
解析:如图,连接BE,BP.∵ΔABC是等边三角形,D是BC的中点,∴AD⊥BC,PC=PB.
∴EP+CP=PB+PE≥BE,即BE就是EP+CP的最小值.
∵ΔABC是等边三角形,E是边AC的中点,AD=5,∴BE=AD=5.∴EP+CP的最小值是5.答案:C
解题策略:等边三角形、等腰三角形以及正方形是轴对称图形,某些顶点的对称点与该图形上的点是重合的,利用这个性质可以解决线段和的最小值问题.
变式练习:
1、如图,在ΔABC中,AB=AC,AD,CE是ΔABC的两条中线,P是AD上一动点,则下列线段的长度等于PB+PE的最小值的是( B )
BC B.CE C.AD D.AC
2、如图,在RtΔABC中,∠C=90°,∠B=30°,BC=16,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是 16
题型二、周长最小值问题
例2、如图,∠AOB=30°,点P为∠AOB内一点,OP=10,点M,N分别在OA,OB上,求ΔPMN周长的最小值.
解:分别作点P关于OA,OB的对称点P1,P2,连接P1P2,交OA于点M,交OB于点N,连接PM,PN,此时,ΔPMN的周长最小,ΔPMN的周长=P1P2,P1P2=OP1=OP2=OP=10.
解题策略:求三角形周长的最小值,一般是利用轴对称将三边转化到一条直线上解决.
变式练习:
3、如图,在四边形ABCD中,∠BAD=121°,∠B=∠D=90°,在BC,CD上分别找到点M,N,使ΔAMN的周长最小,则此时∠AMN+∠ANM的度数为( A )
A.118° B.121° C.120° D.90°
4、如图,ΔABC是等边三角形,AD=AB,E,F分别为边AC,BC上的动点,当ΔDEF的周长最小时,∠FDE的度数是 60°
5、如图,在平面直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在一条直线上,当ΔABC的周长最小时,点C的坐标是 (0,3)
当堂练习
1.如图,点P是直线a外一点,A,B,C,D都是直线a上的点,PBLa,下列线段中最短的是( B )
A.PA B.PB C.PC D.PD
2.如图,∠BAC=30°,AB=2,点P是射线AC上一动点,则线段BP的最小值为 1
3.如图,在ΔABC中,∠ACB=90°,AC=8,BC=6,AB=10.点E是AB上一动点,则CE的最小值为 4.8
解:作CF⊥AB于点F,当E与F重合时,CE最小,面积法可求CF=4.8.
运用两点之间线段最短求最值
4.如图,直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个供水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( D )
5.如图,在ΔABC中,ABLAC,AB=3,BC=5,AC=4,EF为BC的垂直平分线,点P为直线EF上的任意一点,则ΔABP周长的最小值是( C )
A.12 B.6 C.7 D.8
6.如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( C )
A.(-2,0) C.(2,0) B.(4,0) D.(0,0)
7.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题(用直尺画图).
(1)画出格点ΔABC(顶点均在格点上)关于直线DE对称的ΔA1B1C1;
(2)在DE上画出点P,使PB1+PC最小;
(3)在DE上画出点Q,使QA+QC最小.
解:略.
8.如图,要在一条河上架一座桥MN(河的两岸互相平行,桥与河岸垂直),在如下四种方案中,使得E,F两地的路程最短的是( B )
9.如图,点A,B在直线l的同侧,在直线l上求作一点P,使|PB-PA|的值最大.
解:连接BA并延长交直线l于点P.
10.如图,点A,B在直线l的两侧,在直线l上求一点作P,使|PA-PB|的值最大.
解:作点A关于直线l的对称点A',连接A'B并延长交直线l于点P.
11.如图,在RtΔABC中,∠BAC=30°,∠ACB=90°,AC=3,E为AB的中点,在线段AC上找一点H,使得BH+EH的值最小,并求出该最小值. B
解:作点E关于AC的对称点F,连接BF,交AC于点H,此时BH+EH最小,最小值为线段BF的长.易证ΔABF≌ΔBAC,∴BF=AC=3,故BH+EH的最小值为3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
13.4 课题学习 最短路径
知识要点:
两点之间的所有连线中, 最短.
2.连接直线外一点与直线上各点的所有线段中, 最短.
易错点睛:
如图,A,B在直线l异侧,在直线l上取一点P,使PA+PB最小.
【点睛】易模仿课本上的解法而出错.
典例讲解:
题型一、线段和的最小值问题
例1、如图,在等边三角形ABC中,E是边AC的中点,AD是边BC上的中线,P是AD上的动点.若AD=5,则EP+CP的最小值为( )
A.2 B.4 C.5 D.7
解题策略:等边三角形、等腰三角形以及正方形是轴对称图形,某些顶点的对称点与该图形上的点是重合的,利用这个性质可以解决线段和的最小值问题.
变式练习:
如图,在ΔABC中,AB=AC,AD,CE是ΔABC的两条中线,P是AD上一动点,则下列线段的长度等于PB+PE的最小值的是( )
BC B.CE C.AD D.AC
2、如图,在RtΔABC中,∠C=90°,∠B=30°,BC=16,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是 ______
题型二、周长最小值问题
例2、如图,∠AOB=30°,点P为∠AOB内一点,OP=10,点M,N分别在OA,OB上,求ΔPMN周长的最小值.
变式练习:
3、如图,在四边形ABCD中,∠BAD=121°,∠B=∠D=90°,在BC,CD上分别找到点M,N,使ΔAMN的周长最小,则此时∠AMN+∠ANM的度数为( )
A.118° B.121° C.120° D.90°
4、如图,ΔABC是等边三角形,AD=AB,E,F分别为边AC,BC上的动点,当ΔDEF的周长最小时,∠FDE的度数是
5、如图,在平面直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在一条直线上,当ΔABC的周长最小时,点C的坐标是 _________
当堂练习
如图,点P是直线a外一点,A,B,C,D都是直线a上的点,PBLa,下列线段中最短的是( )
A.PA B.PB C.PC D.PD
2.如图,∠BAC=30°,AB=2,点P是射线AC上一动点,则线段BP的最小值为 1
3.如图,在ΔABC中,∠ACB=90°,AC=8,BC=6,AB=10.点E是AB上一动点,则CE的最小值为 ______
4.如图,直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个供水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( )
5.如图,在ΔABC中,ABLAC,AB=3,BC=5,AC=4,EF为BC的垂直平分线,点P为直线EF上的任意一点,则ΔABP周长的最小值是( )
A.12 B.6 C.7 D.8
如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )
A.(-2,0) C.(2,0) B.(4,0) D.(0,0)
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题(用直尺画图).
(1)画出格点ΔABC(顶点均在格点上)关于直线DE对称的ΔA1B1C1;
(2)在DE上画出点P,使PB1+PC最小;
(3)在DE上画出点Q,使QA+QC最小.
如图,要在一条河上架一座桥MN(河的两岸互相平行,桥与河岸垂直),在如下四种方案中,使得E,F两地的路程最短的是( )
9.如图,点A,B在直线l的同侧,在直线l上求作一点P,使|PB-PA|的值最大.
10.如图,点A,B在直线l的两侧,在直线l上求一点作P,使|PA-PB|的值最大.
解:作点A关于直线l的对称点A',连接A'B并延长交直线l于点P.
如图,在RtΔABC中,∠BAC=30°,∠ACB=90°,AC=3,E为AB的中点,在线段AC上找一点H,使得BH+EH的值最小,并求出该最小值.
答案:
知识要点:
两点之间的所有连线中, 线段 最短.
2.连接直线外一点与直线上各点的所有线段中,垂线段 最短.
易错点睛:
如图,A,B在直线l异侧,在直线l上取一点P,使PA+PB最小.
【点睛】易模仿课本上的解法而出错.
【解】 连接AB交直线l于P.运用垂线段最短求最值
典例讲解:
题型一、线段和的最小值问题
例1、如图,在等边三角形ABC中,E是边AC的中点,AD是边BC上的中线,P是AD上的动点.若AD=5,则EP+CP的最小值为( )
A.2 B.4 C.5 D.7
解析:如图,连接BE,BP.∵ΔABC是等边三角形,D是BC的中点,∴AD⊥BC,PC=PB.
∴EP+CP=PB+PE≥BE,即BE就是EP+CP的最小值.
∵ΔABC是等边三角形,E是边AC的中点,AD=5,∴BE=AD=5.∴EP+CP的最小值是5.答案:C
解题策略:等边三角形、等腰三角形以及正方形是轴对称图形,某些顶点的对称点与该图形上的点是重合的,利用这个性质可以解决线段和的最小值问题.
变式练习:
1、如图,在ΔABC中,AB=AC,AD,CE是ΔABC的两条中线,P是AD上一动点,则下列线段的长度等于PB+PE的最小值的是( B )
BC B.CE C.AD D.AC
2、如图,在RtΔABC中,∠C=90°,∠B=30°,BC=16,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是 16
题型二、周长最小值问题
例2、如图,∠AOB=30°,点P为∠AOB内一点,OP=10,点M,N分别在OA,OB上,求ΔPMN周长的最小值.
解:分别作点P关于OA,OB的对称点P1,P2,连接P1P2,交OA于点M,交OB于点N,连接PM,PN,此时,ΔPMN的周长最小,ΔPMN的周长=P1P2,P1P2=OP1=OP2=OP=10.
解题策略:求三角形周长的最小值,一般是利用轴对称将三边转化到一条直线上解决.
变式练习:
3、如图,在四边形ABCD中,∠BAD=121°,∠B=∠D=90°,在BC,CD上分别找到点M,N,使ΔAMN的周长最小,则此时∠AMN+∠ANM的度数为( A )
A.118° B.121° C.120° D.90°
4、如图,ΔABC是等边三角形,AD=AB,E,F分别为边AC,BC上的动点,当ΔDEF的周长最小时,∠FDE的度数是 60°
5、如图,在平面直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在一条直线上,当ΔABC的周长最小时,点C的坐标是 (0,3)
当堂练习
1.如图,点P是直线a外一点,A,B,C,D都是直线a上的点,PBLa,下列线段中最短的是( B )
A.PA B.PB C.PC D.PD
2.如图,∠BAC=30°,AB=2,点P是射线AC上一动点,则线段BP的最小值为 1
3.如图,在ΔABC中,∠ACB=90°,AC=8,BC=6,AB=10.点E是AB上一动点,则CE的最小值为 4.8
解:作CF⊥AB于点F,当E与F重合时,CE最小,面积法可求CF=4.8.
运用两点之间线段最短求最值
4.如图,直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个供水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( D )
5.如图,在ΔABC中,ABLAC,AB=3,BC=5,AC=4,EF为BC的垂直平分线,点P为直线EF上的任意一点,则ΔABP周长的最小值是( C )
A.12 B.6 C.7 D.8
6.如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( C )
A.(-2,0) C.(2,0) B.(4,0) D.(0,0)
7.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题(用直尺画图).
(1)画出格点ΔABC(顶点均在格点上)关于直线DE对称的ΔA1B1C1;
(2)在DE上画出点P,使PB1+PC最小;
(3)在DE上画出点Q,使QA+QC最小.
解:略.
8.如图,要在一条河上架一座桥MN(河的两岸互相平行,桥与河岸垂直),在如下四种方案中,使得E,F两地的路程最短的是( B )
9.如图,点A,B在直线l的同侧,在直线l上求作一点P,使|PB-PA|的值最大.
解:连接BA并延长交直线l于点P.
10.如图,点A,B在直线l的两侧,在直线l上求一点作P,使|PA-PB|的值最大.
解:作点A关于直线l的对称点A',连接A'B并延长交直线l于点P.
11.如图,在RtΔABC中,∠BAC=30°,∠ACB=90°,AC=3,E为AB的中点,在线段AC上找一点H,使得BH+EH的值最小,并求出该最小值. B
解:作点E关于AC的对称点F,连接BF,交AC于点H,此时BH+EH最小,最小值为线段BF的长.易证ΔABF≌ΔBAC,∴BF=AC=3,故BH+EH的最小值为3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
