2021-2022学年人教版数学九年级下册 26.1反比例函数 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册 26.1反比例函数 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 345.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 18:14:02 | ||
图片预览

文档简介
人教版初中数学九年级下同步练习:26.1反比例函数
一、选择题
反比例函数 在第一象限的图象如图所示,则 的值可能是
A. B. C. D.
下列函数中,反比例函数是
A. B.
C. D.
如图,在平面直角坐标系中,菱形 的边 在 轴的正半轴上,反比例函数 的图象经过对角线 的中点 和顶点 .若菱形 的面积为 ,则 的值为
A. B. C. D.
函数 和 在同一直角坐标系中的大致图象是
A. B. C. D.
已知点 在双曲线 上,点 在直线 上,且 , 两点关于 轴对称,设点 的坐标为 ,则 的值是
A. B. C. D.
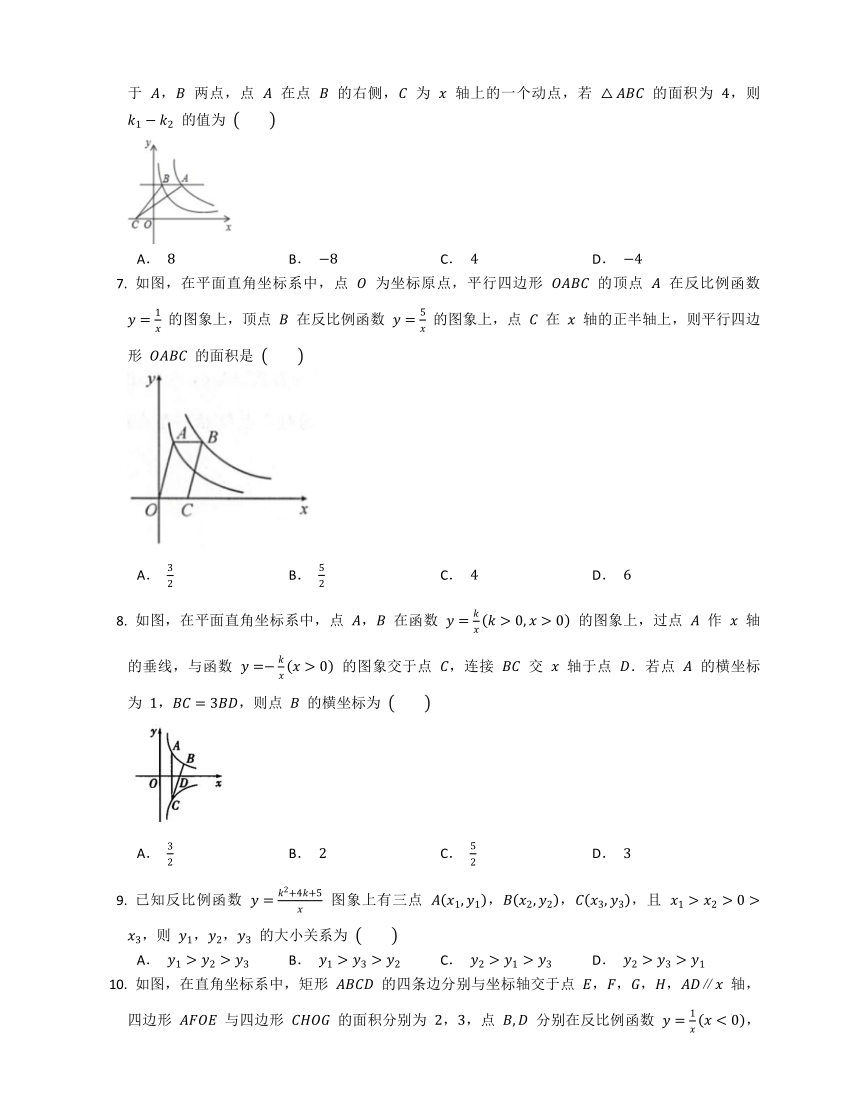
如图,平行于 轴的直线与函数 , 的图象分别相交于 , 两点,点 在点 的右侧, 为 轴上的一个动点,若 的面积为 ,则 的值为
A. B. C. D.
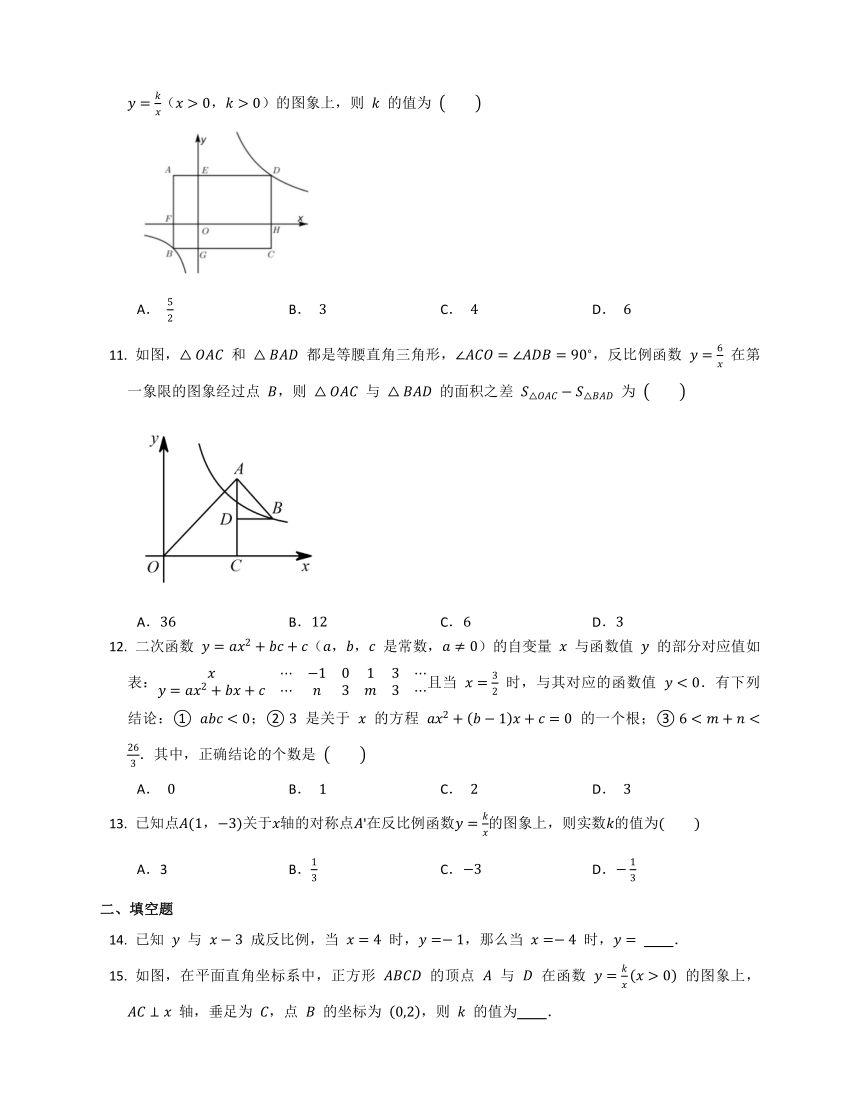
如图,在平面直角坐标系中,点 为坐标原点,平行四边形 的顶点 在反比例函数 的图象上,顶点 在反比例函数 的图象上,点 在 轴的正半轴上,则平行四边形 的面积是
A. B. C. D.
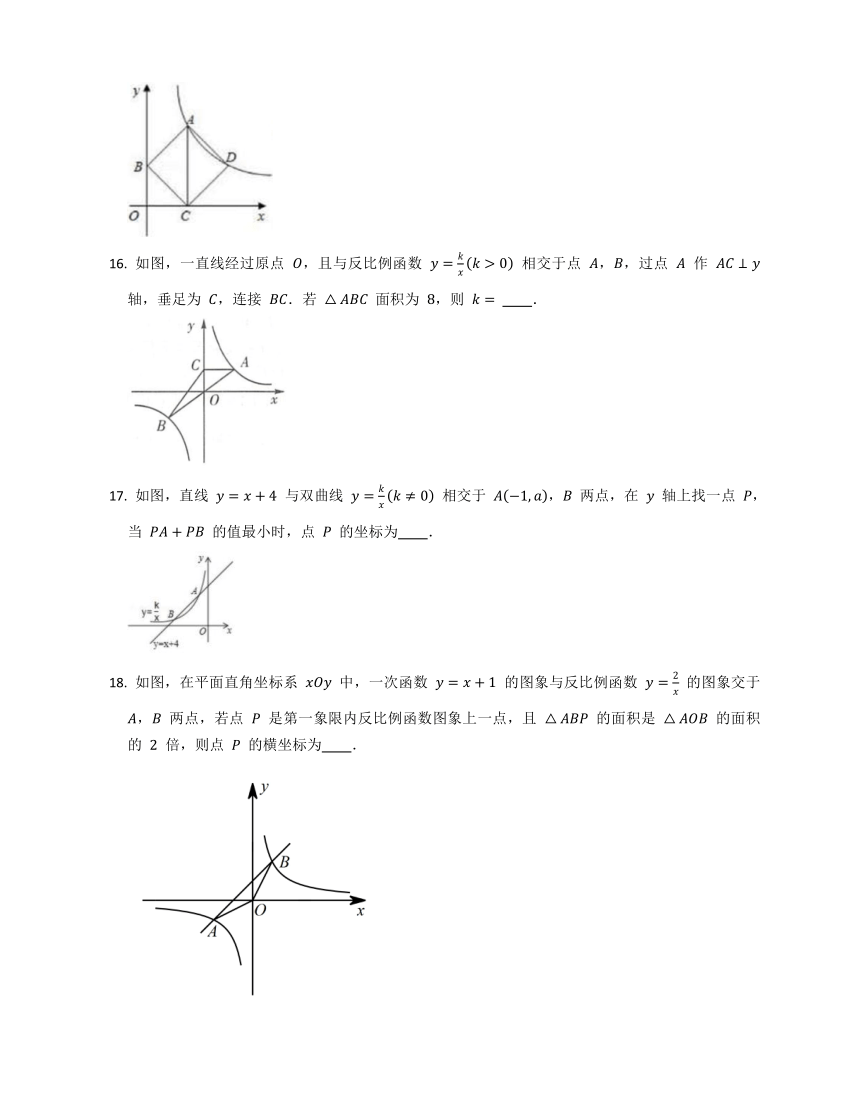
如图,在平面直角坐标系中,点 , 在函数 的图象上,过点 作 轴的垂线,与函数 的图象交于点 ,连接 交 轴于点 .若点 的横坐标为 ,,则点 的横坐标为
A. B. C. D.
已知反比例函数 图象上有三点 ,,,且 ,则 ,, 的大小关系为
A. B. C. D.
如图,在直角坐标系中,矩形 的四条边分别与坐标轴交于点 ,,,, 轴,四边形 与四边形 的面积分别为 ,,点 分别在反比例函数 ,(,)的图象上,则 的值为
A. B. C. D.
如图, 和 都是等腰直角三角形,,反比例函数 在第一象限的图象经过点 ,则 与 的面积之差 为
A. B. C. D.
二次函数 (,, 是常数,)的自变量 与函数值 的部分对应值如表:且当 时,与其对应的函数值 .有下列结论:① ;② 是关于 的方程 的一个根;③ .其中,正确结论的个数是
A. B. C. D.
已知点,关于轴的对称点'在反比例函数的图象上,则实数的值为
A.3 B. C. D.
二、填空题
已知 与 成反比例,当 时,,那么当 时, .
如图,在平面直角坐标系中,正方形 的顶点 与 在函数 的图象上, 轴,垂足为 ,点 的坐标为 ,则 的值为 .
如图,一直线经过原点 ,且与反比例函数 相交于点 ,,过点 作 轴,垂足为 ,连接 .若 面积为 ,则 .
如图,直线 与双曲线 相交于 , 两点,在 轴上找一点 ,当 的值最小时,点 的坐标为 .
如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象交于 , 两点,若点 是第一象限内反比例函数图象上一点,且 的面积是 的面积的 倍,则点 的横坐标为 .
三、解答题
已知一艘轮船上装有 吨货物,轮船到达目的地后开始卸货.设平均卸货的速度为 (吨/小时),卸完这批货物所需的时间为 (小时).
(1) 求 关于 的函数解析式;
(2) 若恰好用 小时卸完船上的货物,则平均每小时需要卸货多少吨?
如图,一次函数 的图象 分别与 轴, 轴交于点 ,,与双曲线 交于点 , 是 的中点.
(1) 求直线 的解析式;
(2) 若直线 与 交于点 ,与双曲线交于点 (不同于 ),问 为何值时,?
如图,已知反比例函数 和一次函数 ,其中一次函数的图象经过 , 两点.
(1) 求反比例函数的解析式;
(2) 如图,已知点 在第一象限,且同时在上述两个函数的图象上,求点 的坐标;
(3) 利用()的结果,请问:在 轴上是否存在点 ,使 为等腰三角形?若存在,把符合条件的 点坐标都求出来;若不存在,请说明理由.
已知直线 和抛物线 .
(1) 直线 恒过定点 ,双曲线 过点 ,求 的值.
(2) 若 ,直线 与抛物线 相交于 ,,在 轴上是否存在点 ,使三角形 为等腰三角形,若不存在请说明理由;若存在,请求出 点的坐标.
(3) 若抛物线 与 轴相交于 , 两点,顶点为 ,当 的面积最小时, 与 相交于点 ,,在直线 下方的抛物线 上有一点 ,求出当 的面积最大时 点的坐标.
答案
一、选择题
1.C
2.D
3.C
4.B
5.A
6.A
7.C
8.B
9.C
10.D
11.D
12.C
13.A
二、填空题
14.
15.
16.
17.
18.
三、解答题
19.
(1) 由题意,得 ,即 .
关于 的函数解析式为 .
(2) 将 代入 ,得 .
答:平均每小时需要卸货 吨.
20.
(1) .
(2) 当 时,(提示:过点 作 ).
21.
(1) .
(2) ,.
(3) ,,,.
22.
(1) 直线 可变形为 ,
故直线 恒过点 ,即 ,
双曲线 过点 ,
,
.
(2) 假设存在,当 时,直线 ,抛物线 ,则
解之得 或
故 ,,
,
点 在 轴上,
设 ,
①当 时,,
,
则 ,
解之得 ,
故 .
②当 时,,
解之得 ,
故 ,
③当 时,,
解之得 或 ,
时 与 重合,
,
综上所述,.
(3) 令 ,得 ,
解之得 ,,
则 ,
当 时,
故 ,
则 ,
则以 为底 的高为 ,
故当 时, 最小,则直线 ,
抛物线 .
如图所示,平移 ,使 与 只有一个交点即为平移后为 ,
则 为 , 的交点时 的面积最大,
设 为 ,则
整理得 ,则当 时, 点唯一,此时 ,
则
解之得 ,,
故 .
一、选择题
反比例函数 在第一象限的图象如图所示,则 的值可能是
A. B. C. D.
下列函数中,反比例函数是
A. B.
C. D.
如图,在平面直角坐标系中,菱形 的边 在 轴的正半轴上,反比例函数 的图象经过对角线 的中点 和顶点 .若菱形 的面积为 ,则 的值为
A. B. C. D.
函数 和 在同一直角坐标系中的大致图象是
A. B. C. D.
已知点 在双曲线 上,点 在直线 上,且 , 两点关于 轴对称,设点 的坐标为 ,则 的值是
A. B. C. D.
如图,平行于 轴的直线与函数 , 的图象分别相交于 , 两点,点 在点 的右侧, 为 轴上的一个动点,若 的面积为 ,则 的值为
A. B. C. D.
如图,在平面直角坐标系中,点 为坐标原点,平行四边形 的顶点 在反比例函数 的图象上,顶点 在反比例函数 的图象上,点 在 轴的正半轴上,则平行四边形 的面积是
A. B. C. D.
如图,在平面直角坐标系中,点 , 在函数 的图象上,过点 作 轴的垂线,与函数 的图象交于点 ,连接 交 轴于点 .若点 的横坐标为 ,,则点 的横坐标为
A. B. C. D.
已知反比例函数 图象上有三点 ,,,且 ,则 ,, 的大小关系为
A. B. C. D.
如图,在直角坐标系中,矩形 的四条边分别与坐标轴交于点 ,,,, 轴,四边形 与四边形 的面积分别为 ,,点 分别在反比例函数 ,(,)的图象上,则 的值为
A. B. C. D.
如图, 和 都是等腰直角三角形,,反比例函数 在第一象限的图象经过点 ,则 与 的面积之差 为
A. B. C. D.
二次函数 (,, 是常数,)的自变量 与函数值 的部分对应值如表:且当 时,与其对应的函数值 .有下列结论:① ;② 是关于 的方程 的一个根;③ .其中,正确结论的个数是
A. B. C. D.
已知点,关于轴的对称点'在反比例函数的图象上,则实数的值为
A.3 B. C. D.
二、填空题
已知 与 成反比例,当 时,,那么当 时, .
如图,在平面直角坐标系中,正方形 的顶点 与 在函数 的图象上, 轴,垂足为 ,点 的坐标为 ,则 的值为 .
如图,一直线经过原点 ,且与反比例函数 相交于点 ,,过点 作 轴,垂足为 ,连接 .若 面积为 ,则 .
如图,直线 与双曲线 相交于 , 两点,在 轴上找一点 ,当 的值最小时,点 的坐标为 .
如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象交于 , 两点,若点 是第一象限内反比例函数图象上一点,且 的面积是 的面积的 倍,则点 的横坐标为 .
三、解答题
已知一艘轮船上装有 吨货物,轮船到达目的地后开始卸货.设平均卸货的速度为 (吨/小时),卸完这批货物所需的时间为 (小时).
(1) 求 关于 的函数解析式;
(2) 若恰好用 小时卸完船上的货物,则平均每小时需要卸货多少吨?
如图,一次函数 的图象 分别与 轴, 轴交于点 ,,与双曲线 交于点 , 是 的中点.
(1) 求直线 的解析式;
(2) 若直线 与 交于点 ,与双曲线交于点 (不同于 ),问 为何值时,?
如图,已知反比例函数 和一次函数 ,其中一次函数的图象经过 , 两点.
(1) 求反比例函数的解析式;
(2) 如图,已知点 在第一象限,且同时在上述两个函数的图象上,求点 的坐标;
(3) 利用()的结果,请问:在 轴上是否存在点 ,使 为等腰三角形?若存在,把符合条件的 点坐标都求出来;若不存在,请说明理由.
已知直线 和抛物线 .
(1) 直线 恒过定点 ,双曲线 过点 ,求 的值.
(2) 若 ,直线 与抛物线 相交于 ,,在 轴上是否存在点 ,使三角形 为等腰三角形,若不存在请说明理由;若存在,请求出 点的坐标.
(3) 若抛物线 与 轴相交于 , 两点,顶点为 ,当 的面积最小时, 与 相交于点 ,,在直线 下方的抛物线 上有一点 ,求出当 的面积最大时 点的坐标.
答案
一、选择题
1.C
2.D
3.C
4.B
5.A
6.A
7.C
8.B
9.C
10.D
11.D
12.C
13.A
二、填空题
14.
15.
16.
17.
18.
三、解答题
19.
(1) 由题意,得 ,即 .
关于 的函数解析式为 .
(2) 将 代入 ,得 .
答:平均每小时需要卸货 吨.
20.
(1) .
(2) 当 时,(提示:过点 作 ).
21.
(1) .
(2) ,.
(3) ,,,.
22.
(1) 直线 可变形为 ,
故直线 恒过点 ,即 ,
双曲线 过点 ,
,
.
(2) 假设存在,当 时,直线 ,抛物线 ,则
解之得 或
故 ,,
,
点 在 轴上,
设 ,
①当 时,,
,
则 ,
解之得 ,
故 .
②当 时,,
解之得 ,
故 ,
③当 时,,
解之得 或 ,
时 与 重合,
,
综上所述,.
(3) 令 ,得 ,
解之得 ,,
则 ,
当 时,
故 ,
则 ,
则以 为底 的高为 ,
故当 时, 最小,则直线 ,
抛物线 .
如图所示,平移 ,使 与 只有一个交点即为平移后为 ,
则 为 , 的交点时 的面积最大,
设 为 ,则
整理得 ,则当 时, 点唯一,此时 ,
则
解之得 ,,
故 .
