2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.4.1第三课时空间中直线、平面的垂直课件(18张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.4.1第三课时空间中直线、平面的垂直课件(18张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 12:02:09 | ||
图片预览






文档简介
(共18张PPT)
1.4.1第三课时 空间中
直线、平面的垂直
新课程标准解读 核心素养
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系
2.能用向量方法判断或证明直线、平面间的垂直关系
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.(数学抽象)
2.能用向量方法证明必修内容中有关直线、平面垂直关系的判定定理.(逻辑推理)
3.能用向量方法证明空间中直线、平面的垂直关系.(逻辑推理)
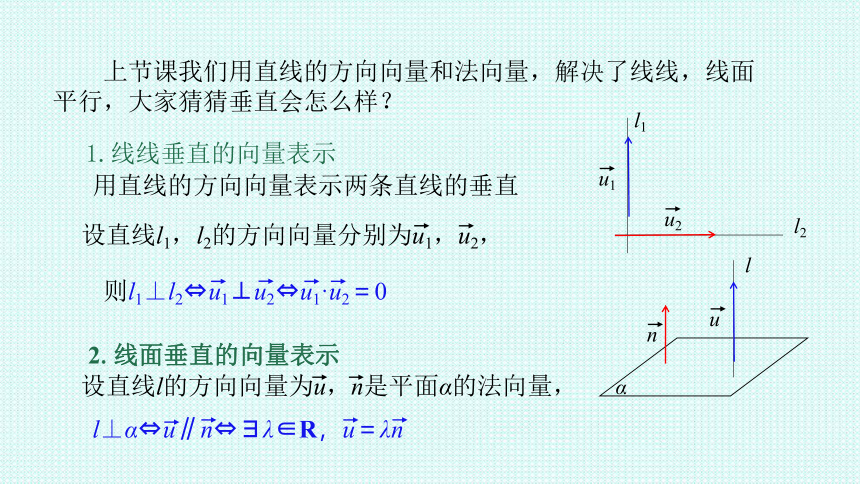
上节课我们用直线的方向向量和法向量,解决了线线,线面平行,大家猜猜垂直会怎么样?
1.线线垂直的向量表示
用直线的方向向量表示两条直线的垂直
设直线l1,l2的方向向量分别为u1,u2,
则l1⊥l2 u1⊥u2 u1·u2=0
l1
u1
l2
u2
2.线面垂直的向量表示
设直线l的方向向量为u,n是平面α的法向量,
l⊥α u∥n λ∈R,u=λn
α
n
l
u
3.面面垂直的向量表示
设n1,n2分别是平面α,β的法向量,则
α⊥β n1⊥n2 n1·n2=0.
n1
n2
怎样用语言叙述利用直线的方向向量与平面的法向量判断垂直关系?
提示:(1)若证线线垂直,则证直线的方向向量垂直;
(2)若证线面垂直,则证直线的方向向量与平面的法向量平行;
(3)若证面面垂直,则证两平面的法向量垂直.
题型一
利用向量方法证明线线垂直
例1如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,点F是PB的中点,点E在边BC上移动.求证:无论点E在边BC上的何处,都有PE⊥AF.
B
A
C
D
P
E
F
方法1:以A为原点,以AD,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
x
y
z
设AD=a,则A(0,0,0),P(0,0,1),B(0,1,0),C(a,1,0),
∵E在BC上,∴设E(m,1,0),
∴无论点E在边BC上何处,总有PE⊥AF.
B
A
C
D
P
E
F
故无论点E在边BC上的何处,都有PE⊥AF.
[规律方法] 利用向量方法证明线线垂直的方法
(1)坐标法:建立空间直角坐标系,写出相关点的坐标,求出两直线方向向量的坐标,然后通过数量积的坐标运算法则证明数量积等于0,从而证明两条直线的方向向量互相垂直.
(2)基向量法:利用空间向量的加法、减法、数乘运算及其运算律,结合图形,将两直线所在的向量用基向量表示,然后根据数量积的运算律证明两直线所在的向量的数量积等于0,从而证明两条直线的方向向量互相垂直.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.求证:EF⊥BC.
A
B
C
D
E
F
由题意,以点B为坐标原点,在平面DBC内过点B作垂直于BC的直线为x轴,BC所在直线为y轴,在平面ABC内过点B作垂直BC的直线为z轴,建立如图所示的空间直角坐标系,
x
y
z
题型二
利用向量方法证明线面垂直
例2在棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别为棱AB,BC,B1B的中点.求证:D1M⊥平面EFB1.
方法1:因为E,F,M分别为棱AB,BC,B1B的中点,
C
D
A1
B1
C1
D1
A
B
M
E
F
如图所示,在正方体ABCD A1B1C1D1中,E,F分别是BB1,D1B1的中点.求证:EF⊥平面B1AC.
C
D
A1
B1
C1
D1
A
B
E
F
设正方体的棱长为2a,建立如图所示的空间直角坐标系.
则A(2a,0,0),C(0,2a,0),B1(2a,2a,2a),
E(2a,2a,a),F(a,a,2a).
x
y
z
∴ EF=(-a,-a,a),AB1=(0,2a,2a), AC=(-2a,2a,0).
∵EF·AB1=(-a,-a,a)·(0,2a,2a)=(-a)×0+(-a)×2a+a×2a=0,
EF·AC=(-a,-a,a)·(-2a,2a,0)=2a2-2a2+0=0,
∴EF⊥AB1,EF⊥AC.又AB1∩AC=A,∴EF⊥平面B1AC.
用向量法证明线面垂直的方法及步骤
(1)利用线线垂直:①将直线的方向向量用坐标表示;②找出平面内两条相交直线,并用坐标表示它们的方向向量;③判断直线的方向向量与平面内两条直线的方向向量垂直;
(2)利用平面的法向量:①将直线的方向向量用坐标表示;②求出平面的法向量;③判断直线的方向向量与平面的法向量平行.
如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.
求证:AB1⊥平面A1BD.
A
B
C
A1
B1
C1
D
O
x
y
z
O1
即AB1⊥BA1,AB1⊥BD.又因为BA1∩BD=B,所以AB1⊥平面A1BD.
A
B
C
A1
B1
C1
D
O
x
O1
y
z
方法二:设平面A1BD的法向量为n=(x,y,z),
题型三
利用向量方法证明面面垂直
例3如图所示,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=2,BB1=1,点E为BB1的中点,证明:平面AEC1⊥平面AA1C1C.
A
B
C
A1
B1
C1
E
由题意得AB,BC,B1B两两垂直.以点B为原点,BA,BC,BB1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系.
x
y
z
设平面AA1C1C的一个法向量为n1=(x1,y1,z1).
设平面AEC1的一个法向量为n2=(x2,y2,z2).
∵n1·n2=1×1+1×(-1)+0×4=0,
∴n1⊥n2,∴平面AEC1⊥平面AA1C1C.
[规律方法] 1.利用空间向量证明面面垂直通常有两个途径:一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直;二是直接求解两个平面的法向量,由两个法向量垂直,得面面垂直.
2.向量法证明面面垂直的优越性主要体现在不必考虑图形的位置关系,恰当建系或用基向量表示后,只需经过向量运算就可得到要证明的结果,思路方法“公式化”,降低了思维难度.
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=,AB=AC=2A1C1=2,D为BC的中点. 证明:平面A1AD⊥平面BCC1B1.
A
B
C
A1
B1
C1
D
如图,建立空间直角坐标系,
x
y
z
因为D为BC的中点,所以D点坐标为(1,1,0),
设平面A1AD的法向量n1=(x1,y1,z1),平面BCC1B1的法向量为
n2=(x2,y2,z2).
所以n1·n2=1-1+0=0,
所以n1⊥n2,所以平面A1AD⊥平面BCC1B1.
A
B
C
A1
B1
C1
D
x
y
z
1.4.1第三课时 空间中
直线、平面的垂直
新课程标准解读 核心素养
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系
2.能用向量方法判断或证明直线、平面间的垂直关系
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.(数学抽象)
2.能用向量方法证明必修内容中有关直线、平面垂直关系的判定定理.(逻辑推理)
3.能用向量方法证明空间中直线、平面的垂直关系.(逻辑推理)
上节课我们用直线的方向向量和法向量,解决了线线,线面平行,大家猜猜垂直会怎么样?
1.线线垂直的向量表示
用直线的方向向量表示两条直线的垂直
设直线l1,l2的方向向量分别为u1,u2,
则l1⊥l2 u1⊥u2 u1·u2=0
l1
u1
l2
u2
2.线面垂直的向量表示
设直线l的方向向量为u,n是平面α的法向量,
l⊥α u∥n λ∈R,u=λn
α
n
l
u
3.面面垂直的向量表示
设n1,n2分别是平面α,β的法向量,则
α⊥β n1⊥n2 n1·n2=0.
n1
n2
怎样用语言叙述利用直线的方向向量与平面的法向量判断垂直关系?
提示:(1)若证线线垂直,则证直线的方向向量垂直;
(2)若证线面垂直,则证直线的方向向量与平面的法向量平行;
(3)若证面面垂直,则证两平面的法向量垂直.
题型一
利用向量方法证明线线垂直
例1如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,点F是PB的中点,点E在边BC上移动.求证:无论点E在边BC上的何处,都有PE⊥AF.
B
A
C
D
P
E
F
方法1:以A为原点,以AD,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
x
y
z
设AD=a,则A(0,0,0),P(0,0,1),B(0,1,0),C(a,1,0),
∵E在BC上,∴设E(m,1,0),
∴无论点E在边BC上何处,总有PE⊥AF.
B
A
C
D
P
E
F
故无论点E在边BC上的何处,都有PE⊥AF.
[规律方法] 利用向量方法证明线线垂直的方法
(1)坐标法:建立空间直角坐标系,写出相关点的坐标,求出两直线方向向量的坐标,然后通过数量积的坐标运算法则证明数量积等于0,从而证明两条直线的方向向量互相垂直.
(2)基向量法:利用空间向量的加法、减法、数乘运算及其运算律,结合图形,将两直线所在的向量用基向量表示,然后根据数量积的运算律证明两直线所在的向量的数量积等于0,从而证明两条直线的方向向量互相垂直.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.求证:EF⊥BC.
A
B
C
D
E
F
由题意,以点B为坐标原点,在平面DBC内过点B作垂直于BC的直线为x轴,BC所在直线为y轴,在平面ABC内过点B作垂直BC的直线为z轴,建立如图所示的空间直角坐标系,
x
y
z
题型二
利用向量方法证明线面垂直
例2在棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别为棱AB,BC,B1B的中点.求证:D1M⊥平面EFB1.
方法1:因为E,F,M分别为棱AB,BC,B1B的中点,
C
D
A1
B1
C1
D1
A
B
M
E
F
如图所示,在正方体ABCD A1B1C1D1中,E,F分别是BB1,D1B1的中点.求证:EF⊥平面B1AC.
C
D
A1
B1
C1
D1
A
B
E
F
设正方体的棱长为2a,建立如图所示的空间直角坐标系.
则A(2a,0,0),C(0,2a,0),B1(2a,2a,2a),
E(2a,2a,a),F(a,a,2a).
x
y
z
∴ EF=(-a,-a,a),AB1=(0,2a,2a), AC=(-2a,2a,0).
∵EF·AB1=(-a,-a,a)·(0,2a,2a)=(-a)×0+(-a)×2a+a×2a=0,
EF·AC=(-a,-a,a)·(-2a,2a,0)=2a2-2a2+0=0,
∴EF⊥AB1,EF⊥AC.又AB1∩AC=A,∴EF⊥平面B1AC.
用向量法证明线面垂直的方法及步骤
(1)利用线线垂直:①将直线的方向向量用坐标表示;②找出平面内两条相交直线,并用坐标表示它们的方向向量;③判断直线的方向向量与平面内两条直线的方向向量垂直;
(2)利用平面的法向量:①将直线的方向向量用坐标表示;②求出平面的法向量;③判断直线的方向向量与平面的法向量平行.
如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.
求证:AB1⊥平面A1BD.
A
B
C
A1
B1
C1
D
O
x
y
z
O1
即AB1⊥BA1,AB1⊥BD.又因为BA1∩BD=B,所以AB1⊥平面A1BD.
A
B
C
A1
B1
C1
D
O
x
O1
y
z
方法二:设平面A1BD的法向量为n=(x,y,z),
题型三
利用向量方法证明面面垂直
例3如图所示,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=2,BB1=1,点E为BB1的中点,证明:平面AEC1⊥平面AA1C1C.
A
B
C
A1
B1
C1
E
由题意得AB,BC,B1B两两垂直.以点B为原点,BA,BC,BB1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系.
x
y
z
设平面AA1C1C的一个法向量为n1=(x1,y1,z1).
设平面AEC1的一个法向量为n2=(x2,y2,z2).
∵n1·n2=1×1+1×(-1)+0×4=0,
∴n1⊥n2,∴平面AEC1⊥平面AA1C1C.
[规律方法] 1.利用空间向量证明面面垂直通常有两个途径:一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直;二是直接求解两个平面的法向量,由两个法向量垂直,得面面垂直.
2.向量法证明面面垂直的优越性主要体现在不必考虑图形的位置关系,恰当建系或用基向量表示后,只需经过向量运算就可得到要证明的结果,思路方法“公式化”,降低了思维难度.
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=,AB=AC=2A1C1=2,D为BC的中点. 证明:平面A1AD⊥平面BCC1B1.
A
B
C
A1
B1
C1
D
如图,建立空间直角坐标系,
x
y
z
因为D为BC的中点,所以D点坐标为(1,1,0),
设平面A1AD的法向量n1=(x1,y1,z1),平面BCC1B1的法向量为
n2=(x2,y2,z2).
所以n1·n2=1-1+0=0,
所以n1⊥n2,所以平面A1AD⊥平面BCC1B1.
A
B
C
A1
B1
C1
D
x
y
z
