2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率课件(18张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率课件(18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 12:07:20 | ||
图片预览




文档简介
(共18张PPT)
2.1.1倾斜角与斜率
新课程标准解读 核心素养
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.
2.理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程.
3.掌握过两点的直线斜率的计算公式.
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.(数学抽象)
2.理解直线的倾斜角和斜率的概念.(数学抽象)
3.掌握倾斜角和斜率之间的关系.(逻辑推理)
4.掌握过两点的直线斜率的计算公式.(数学运算)
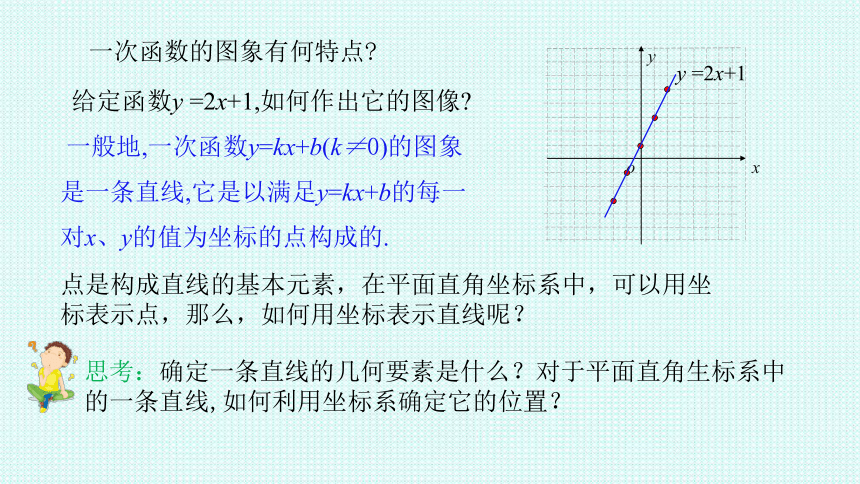
一次函数的图象有何特点
给定函数y =2x+1,如何作出它的图像
一般地,一次函数y=kx+b(k≠0)的图象
是一条直线,它是以满足y=kx+b的每一
对x、y的值为坐标的点构成的.
x
y
o
y =2x+1
点是构成直线的基本元素,在平面直角坐标系中,可以用坐标表示点,那么,如何用坐标表示直线呢?
思考:确定一条直线的几何要素是什么?对于平面直角生标系中的一条直线,如何利用坐标系确定它的位置?
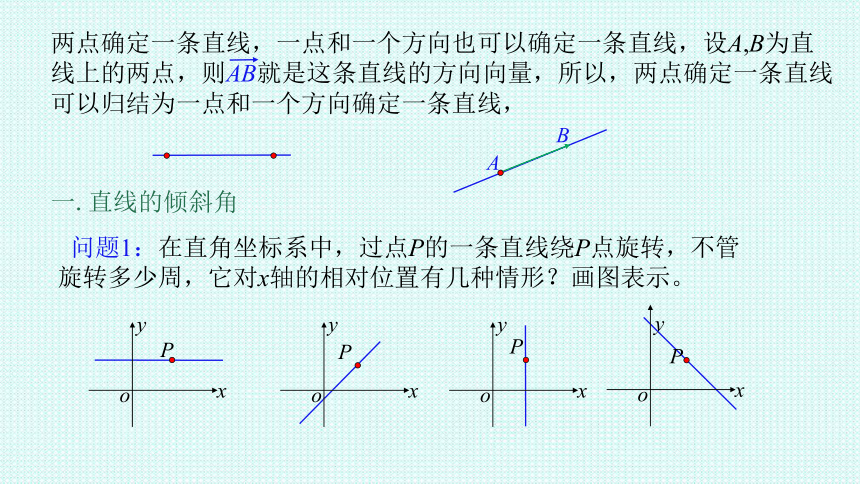
两点确定一条直线,一点和一个方向也可以确定一条直线,设A,B为直线上的两点,则AB就是这条直线的方向向量,所以,两点确定一条直线可以归结为一点和一个方向确定一条直线,
A
B
一.直线的倾斜角
问题1:在直角坐标系中,过点P的一条直线绕P点旋转,不管旋转多少周,它对x轴的相对位置有几种情形?画图表示。
x
o
y
P
x
o
y
P
x
o
y
P
x
o
y
P
O
x
y
P
α
α
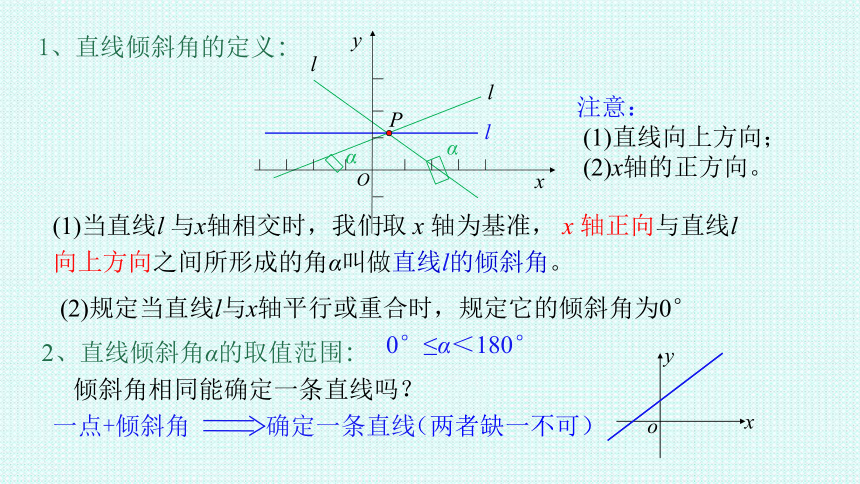
(1)当直线l 与x轴相交时,我们取 x 轴为基准, x 轴正向与直线l 向上方向之间所形成的角α叫做直线l的倾斜角。
l
l
注意:
(1)直线向上方向;
(2)x轴的正方向。
(2)规定当直线l与x轴平行或重合时,规定它的倾斜角为0°
l
1、直线倾斜角的定义:
2、直线倾斜角α的取值范围:
0°≤α<180°
倾斜角相同能确定一条直线吗?
x
o
y
一点+倾斜角 确定一条直线
(两者缺一不可)
3、直线倾斜角的意义
体现了直线对x轴正方向的倾斜程度
①平面直角坐标系中每一条直线都有确定的倾斜角;
②倾斜程度不同的直线有不同的倾斜角;
③倾斜程度相同的直线其倾斜角相同.
思考:日常生活中,还有没有表示倾斜程度的量呢?
x
y
o
α
前进量
升
高
量
“坡度比”
是“倾斜角”
的正切值.
二.直线的斜率
1、直线斜率的定义:
把一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即k=tanα
思考:当直线与x轴垂直时,直线的倾斜角是多少?
x
o
y
倾斜角α=90°, tanα不存在,k不存在
2.斜率与倾斜角的对应关系
倾斜角(范围) α=0° 0°<α<90° α=90° 90°<α<180°
斜率(范围) k=0 k>0 不存在 k<0
下列说法正确的是( )
A .任一条直线都有倾斜角,也都有斜率
B.直线的倾斜角越大,斜率也越大
C .平行于x轴的直线的倾斜角是0°或180°
D. 一定点和一倾斜角可以唯一确定一条直线
已知直线l经过第二、四象限,则直线l的倾斜角α的取值范围是( )
A.0°≤α<90° B.90°≤α<180°
C.90°<α<180° D.0°<α<180°
x
o
y
3、探究:由两点确定的直线的斜率
如果给定直线上两点坐标,直线是确定的,倾斜角也是确定的,斜率就是确定的,那么又怎么求出直线的斜率呢?
经过两点P1(x1,y1),P2(x2,y2)且x1≠x2的直线的斜率k
α为锐角
x
y
o
P1
P2
α
当0°≤α<90°时,k ≥ 0.
α为钝角
x
y
o
P1
P2
α
当90°<α<180°时,k 0.
说明:此公式与两点坐标的顺序无关
公式的特点:
(1)与两点的顺序无关;
(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角;
(3)当x1=x2时,公式不适用,此时直线与x轴垂直,α=900
三、直线的方向向量
P1P2=(x2-x1,y2-y1)=(x2-x1)(1,k)
经过A(2,0),B(0,-1)两点的直线的方向向量为(1,k),则k=________.
探究点1 直线的倾斜角
x
y
o
α
l
l1
α+45°
x
y
o
α
l
当135°≤α<180°时,l1的倾斜角为α-135°
l1
45°-(180°-α)=α-135°
求直线的倾斜角的方法及两点注意
(1)方法:结合图形,利用特殊三角形(如直角三角形)求角;
(2)两点注意:①当直线与x轴平行或重合时,倾斜角为0°,当直线与x轴垂直时,倾斜角为90°;②注意直线倾斜角的取值范围是0°≤α<180°.
如图,直线l的倾斜角为 ( )
A.60° B.120° C.30° D.150°
x
y
o
l
45°
105°
①对顶角相等;②外角等于不相邻的两个内角和.
探究点2 直线斜率的计算
直线AB的倾斜角为0°.
直线BC的倾斜角为60°.
直线AC的倾斜角为30°.
(1)应用斜率公式求斜率时应注意的问题
①运用公式的前提条件是“x1≠x2”,即直线不与x轴垂直,因为当直线与x轴垂直时,斜率不存在.
②斜率公式与两点P1,P2的先后顺序无关,也就是说公式中的x1与x2,y1与y2可以同时交换位置.
(2)在0°≤α<180°范围内的一些特殊角的正切值要熟记.
倾斜角α 0° 30° 45° 60° 120° 135° 150°
斜率k 0 1 -1
探究点3 直线的倾斜角及斜率的应用
x
y
o
1
2
2
-2
P
A
B
当直线l由位置PA绕点P转动到位置PB时,l的斜率逐渐变大直至当l垂直于x轴,当直线l垂直于x轴时,l无斜率,再转动时斜率为负值并逐渐变大直到PB的位置,所以直线l的斜率
(2021·广东江门高一月考)已知A(-3,-5),B(1,3),C(5,11)三点,这三点________(填“是”或“否”)在同一直线上.
因为kAB=kBC,即两条直线的斜率相同,并且它们过同一点B,
所以A,B,C三点在同一直线上.故填是.
1.若经过两点A(2,1),B(1,m2)的直线l的倾斜角为锐角,则m的取值范围是( )
A.(-∞,1) B.(-1,+∞)
C.(-1,1) D.(-∞,-1)∪(1,+∞)
2.经过两点A(m,2),B(-m,2m-1)的直线的倾斜角为45°.若点
C(m+1,n)在直线AB上,求m,n的值.
2.1.1倾斜角与斜率
新课程标准解读 核心素养
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.
2.理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程.
3.掌握过两点的直线斜率的计算公式.
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.(数学抽象)
2.理解直线的倾斜角和斜率的概念.(数学抽象)
3.掌握倾斜角和斜率之间的关系.(逻辑推理)
4.掌握过两点的直线斜率的计算公式.(数学运算)
一次函数的图象有何特点
给定函数y =2x+1,如何作出它的图像
一般地,一次函数y=kx+b(k≠0)的图象
是一条直线,它是以满足y=kx+b的每一
对x、y的值为坐标的点构成的.
x
y
o
y =2x+1
点是构成直线的基本元素,在平面直角坐标系中,可以用坐标表示点,那么,如何用坐标表示直线呢?
思考:确定一条直线的几何要素是什么?对于平面直角生标系中的一条直线,如何利用坐标系确定它的位置?
两点确定一条直线,一点和一个方向也可以确定一条直线,设A,B为直线上的两点,则AB就是这条直线的方向向量,所以,两点确定一条直线可以归结为一点和一个方向确定一条直线,
A
B
一.直线的倾斜角
问题1:在直角坐标系中,过点P的一条直线绕P点旋转,不管旋转多少周,它对x轴的相对位置有几种情形?画图表示。
x
o
y
P
x
o
y
P
x
o
y
P
x
o
y
P
O
x
y
P
α
α
(1)当直线l 与x轴相交时,我们取 x 轴为基准, x 轴正向与直线l 向上方向之间所形成的角α叫做直线l的倾斜角。
l
l
注意:
(1)直线向上方向;
(2)x轴的正方向。
(2)规定当直线l与x轴平行或重合时,规定它的倾斜角为0°
l
1、直线倾斜角的定义:
2、直线倾斜角α的取值范围:
0°≤α<180°
倾斜角相同能确定一条直线吗?
x
o
y
一点+倾斜角 确定一条直线
(两者缺一不可)
3、直线倾斜角的意义
体现了直线对x轴正方向的倾斜程度
①平面直角坐标系中每一条直线都有确定的倾斜角;
②倾斜程度不同的直线有不同的倾斜角;
③倾斜程度相同的直线其倾斜角相同.
思考:日常生活中,还有没有表示倾斜程度的量呢?
x
y
o
α
前进量
升
高
量
“坡度比”
是“倾斜角”
的正切值.
二.直线的斜率
1、直线斜率的定义:
把一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即k=tanα
思考:当直线与x轴垂直时,直线的倾斜角是多少?
x
o
y
倾斜角α=90°, tanα不存在,k不存在
2.斜率与倾斜角的对应关系
倾斜角(范围) α=0° 0°<α<90° α=90° 90°<α<180°
斜率(范围) k=0 k>0 不存在 k<0
下列说法正确的是( )
A .任一条直线都有倾斜角,也都有斜率
B.直线的倾斜角越大,斜率也越大
C .平行于x轴的直线的倾斜角是0°或180°
D. 一定点和一倾斜角可以唯一确定一条直线
已知直线l经过第二、四象限,则直线l的倾斜角α的取值范围是( )
A.0°≤α<90° B.90°≤α<180°
C.90°<α<180° D.0°<α<180°
x
o
y
3、探究:由两点确定的直线的斜率
如果给定直线上两点坐标,直线是确定的,倾斜角也是确定的,斜率就是确定的,那么又怎么求出直线的斜率呢?
经过两点P1(x1,y1),P2(x2,y2)且x1≠x2的直线的斜率k
α为锐角
x
y
o
P1
P2
α
当0°≤α<90°时,k ≥ 0.
α为钝角
x
y
o
P1
P2
α
当90°<α<180°时,k 0.
说明:此公式与两点坐标的顺序无关
公式的特点:
(1)与两点的顺序无关;
(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角;
(3)当x1=x2时,公式不适用,此时直线与x轴垂直,α=900
三、直线的方向向量
P1P2=(x2-x1,y2-y1)=(x2-x1)(1,k)
经过A(2,0),B(0,-1)两点的直线的方向向量为(1,k),则k=________.
探究点1 直线的倾斜角
x
y
o
α
l
l1
α+45°
x
y
o
α
l
当135°≤α<180°时,l1的倾斜角为α-135°
l1
45°-(180°-α)=α-135°
求直线的倾斜角的方法及两点注意
(1)方法:结合图形,利用特殊三角形(如直角三角形)求角;
(2)两点注意:①当直线与x轴平行或重合时,倾斜角为0°,当直线与x轴垂直时,倾斜角为90°;②注意直线倾斜角的取值范围是0°≤α<180°.
如图,直线l的倾斜角为 ( )
A.60° B.120° C.30° D.150°
x
y
o
l
45°
105°
①对顶角相等;②外角等于不相邻的两个内角和.
探究点2 直线斜率的计算
直线AB的倾斜角为0°.
直线BC的倾斜角为60°.
直线AC的倾斜角为30°.
(1)应用斜率公式求斜率时应注意的问题
①运用公式的前提条件是“x1≠x2”,即直线不与x轴垂直,因为当直线与x轴垂直时,斜率不存在.
②斜率公式与两点P1,P2的先后顺序无关,也就是说公式中的x1与x2,y1与y2可以同时交换位置.
(2)在0°≤α<180°范围内的一些特殊角的正切值要熟记.
倾斜角α 0° 30° 45° 60° 120° 135° 150°
斜率k 0 1 -1
探究点3 直线的倾斜角及斜率的应用
x
y
o
1
2
2
-2
P
A
B
当直线l由位置PA绕点P转动到位置PB时,l的斜率逐渐变大直至当l垂直于x轴,当直线l垂直于x轴时,l无斜率,再转动时斜率为负值并逐渐变大直到PB的位置,所以直线l的斜率
(2021·广东江门高一月考)已知A(-3,-5),B(1,3),C(5,11)三点,这三点________(填“是”或“否”)在同一直线上.
因为kAB=kBC,即两条直线的斜率相同,并且它们过同一点B,
所以A,B,C三点在同一直线上.故填是.
1.若经过两点A(2,1),B(1,m2)的直线l的倾斜角为锐角,则m的取值范围是( )
A.(-∞,1) B.(-1,+∞)
C.(-1,1) D.(-∞,-1)∪(1,+∞)
2.经过两点A(m,2),B(-m,2m-1)的直线的倾斜角为45°.若点
C(m+1,n)在直线AB上,求m,n的值.
