2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.3.3点到直线的距离;2.3.4两平行线间的距离课件(16张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.3.3点到直线的距离;2.3.4两平行线间的距离课件(16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 12:13:45 | ||
图片预览



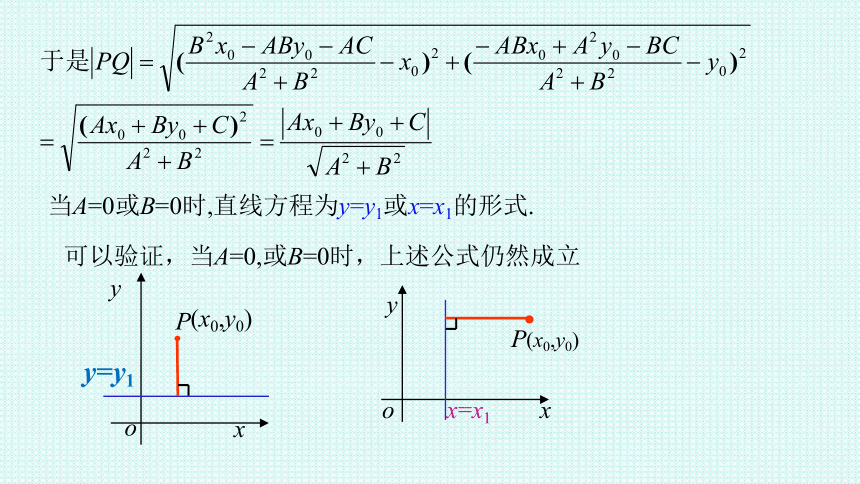
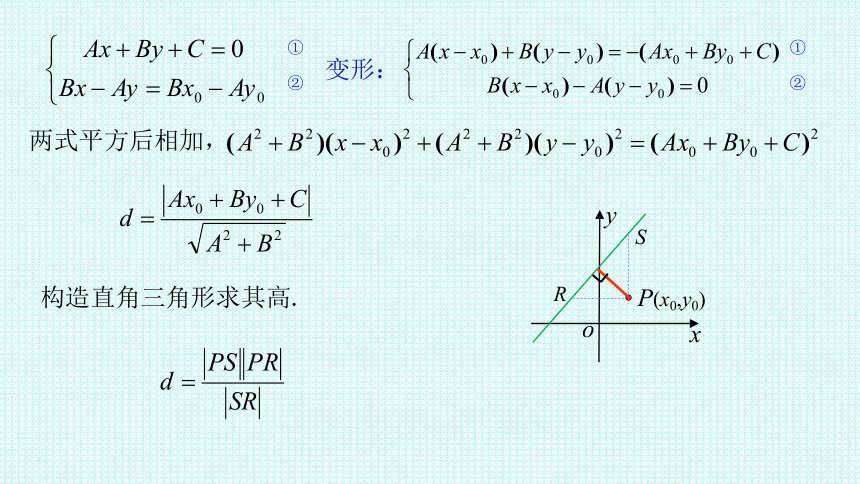

文档简介
(共16张PPT)
2.3.3点到直线的距离
2.3.4两条平行线间的距离
新课程标准解读 核心素养
1.探索并掌握平面上点到直线的距离公式.
2.会求两条平行直线间的距离.
1.掌握点到直线的距离公式.(数学抽象)
2.会求两条平行直线间的距离.(数学运算)
会运用坐标法证明简单的平面几何问题.(数学建模)
在公路附近有一家乡村饭馆,现在需要铺设一条连接饭馆和公路的道路.请同学们帮助设计一下:在理论上怎样铺路可以使这条连接道路的长度最短
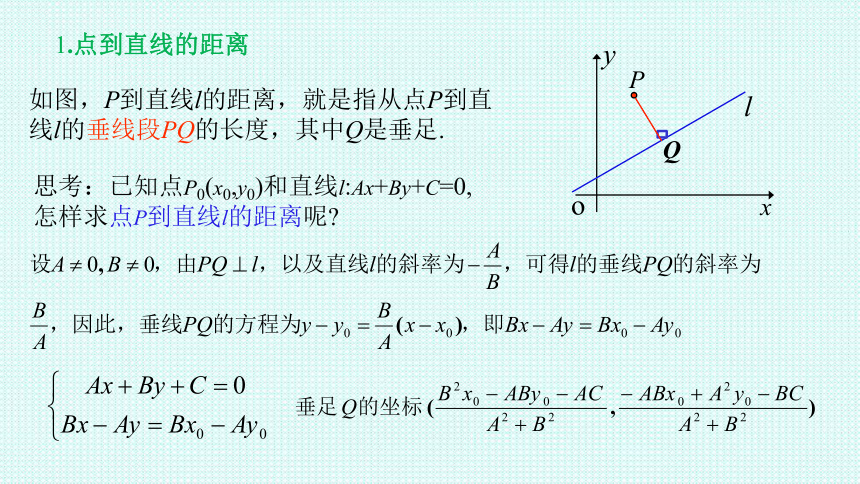
1.点到直线的距离
如图,P到直线l的距离,就是指从点P到直线l的垂线段PQ的长度,其中Q是垂足.
P
y
x
o
l
Q
思考:已知点P0(x0,y0)和直线l:Ax+By+C=0, 怎样求点P到直线l的距离呢
当A=0或B=0时,直线方程为y=y1或x=x1的形式.
可以验证,当A=0,或B=0时,上述公式仍然成立
y
o
y=y1
(x0,y0)
x
P
x
y
o
x=x1
P(x0,y0)
①
②
变形:
①
②
两式平方后相加,
构造直角三角形求其高.
x
y
o
P(x0,y0)
S
R
向量法求点到直线的距离.
x
y
o
P(x0,y0)
M
Q
P1(x1,y1)
P2(x2,y2)
Ax1+By1+C=0,
Ax2+By2+C=0,
A(x2-x1)+B(y2-y1)=0,
向量(A,B)与向量(x2-x1,y2-y1)垂直
n
n= (A,B),
PM=(x-x0,y-y0)
(1)分子是P点坐标代入直线方程;
(2)分母是直线未知数x、y系数平方和的算术根,类似于勾股定理求斜边的长
(3)运用此公式时要注意直线方程必须是一般式,
若给出其他形式,应先化成一般式再用公式.
(4)当点P0在直线l上时,点到直线的距离为零,公式仍然适用.
例1:已知点A(1,3),B(3,1),C(-1,0),求△ABC的面积
x
y
O
A
B
C
解:设AB边上的高为h
AB
=
(3-1)2+(1-3)2
=2
kAB=-1
AB的直线方程为:x+y-4=0
h=
-1+0-4
S= × × =5
1
2
2
5
还有其他的方法吗?
例2:用解析法证明:等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。
O
A(a,0)
C(-a,0)
B(0,b)
x
y
E
F
P
证明:建立如图直角坐标系,设P (x,0),x∈(-a,a )
lAB:bx+ay-ab=0, lCB: bx-ay+ab=0.
|PE|=
|bx-ab|
|PF|=
|bx+ab|
A到BC的距离h=
2ab
因为|PE|+|PF|=h,所以原命题得证。
例3.已知直线l经过点M(-1,2),且A(2,3),B(-4,5)两点到直线l的距离相等,求直线l的方程.
(方法一)当过点M(-1,2)的直线l的斜率不存在时,直线l的方程为x=-1,
恰好A(2,3),B(-4,5)两点到直线l的距离相等,故x=-1满足题意;
当过点M(-1,2)的直线l的斜率存在时,设l的方程为y-2=k(x+1),即kx-y+k+2=0,由A(2,3)与B(-4,5)两点到直线l的距离相等,得
k2+1
|2k-3+k+2|
=
|-4k-5+k+2|
k2+1
k=-
1
3
此时l的方程为y-2=- (x+1)
1
3
即x+3y-5=0.
综上所述,直线l的方程为x=-1
或x+3y-5=0.
(方法二)由题意得l∥AB或l过AB的中点.
当l∥AB时,设直线AB的斜率为kAB,
kAB=
-
1
3
l的方程为x+3y-5=0.
当l过AB的中点(-1,4)时,直线l的方程为x=-1.
综上所述,直线l的方程为x=-1或x+3y-5=0.
2.两条平行直线的距离
求两条平行直线Ax+By+C1=0与Ax+By+C2=0的距离.
x
y
o
l1
l2
P
Q
解:在直线上Ax+By+C1=0任取一点,如P(x0,y0)
则两平行线的距离就是点P(x0, y0)
到直线Ax+By+C2=0 的距离。(如图)
因此,d=
注意
(1)把直线方程化为直线的一般式方程;
(2)两条直线方程中x,y的系数必须分别相等;
(3)两平行线间的距离是一条直线上任一点到另一条直线的距离,也可以看作是两条直线上各取一点的最短距离.
(1)两直线变形为3x-2y-12=0与3x-2y+2=0,d=
(2)由题意得3×(-8)-(-4)×a=0.所以a=6.
c=-28或32.
求与两条平行直线l1:2x-3y+4=0或l2:2x-3y-2=0距离相等的直线l的方程.
设所求直线l的方程为2x-3y+C=0.
由直线l与两条平行线的距离相等,
即|C-4|=|C+2|,解得C=1.
故直线l的方程为2x-3y+1=0.
2.3.3点到直线的距离
2.3.4两条平行线间的距离
新课程标准解读 核心素养
1.探索并掌握平面上点到直线的距离公式.
2.会求两条平行直线间的距离.
1.掌握点到直线的距离公式.(数学抽象)
2.会求两条平行直线间的距离.(数学运算)
会运用坐标法证明简单的平面几何问题.(数学建模)
在公路附近有一家乡村饭馆,现在需要铺设一条连接饭馆和公路的道路.请同学们帮助设计一下:在理论上怎样铺路可以使这条连接道路的长度最短
1.点到直线的距离
如图,P到直线l的距离,就是指从点P到直线l的垂线段PQ的长度,其中Q是垂足.
P
y
x
o
l
Q
思考:已知点P0(x0,y0)和直线l:Ax+By+C=0, 怎样求点P到直线l的距离呢
当A=0或B=0时,直线方程为y=y1或x=x1的形式.
可以验证,当A=0,或B=0时,上述公式仍然成立
y
o
y=y1
(x0,y0)
x
P
x
y
o
x=x1
P(x0,y0)
①
②
变形:
①
②
两式平方后相加,
构造直角三角形求其高.
x
y
o
P(x0,y0)
S
R
向量法求点到直线的距离.
x
y
o
P(x0,y0)
M
Q
P1(x1,y1)
P2(x2,y2)
Ax1+By1+C=0,
Ax2+By2+C=0,
A(x2-x1)+B(y2-y1)=0,
向量(A,B)与向量(x2-x1,y2-y1)垂直
n
n= (A,B),
PM=(x-x0,y-y0)
(1)分子是P点坐标代入直线方程;
(2)分母是直线未知数x、y系数平方和的算术根,类似于勾股定理求斜边的长
(3)运用此公式时要注意直线方程必须是一般式,
若给出其他形式,应先化成一般式再用公式.
(4)当点P0在直线l上时,点到直线的距离为零,公式仍然适用.
例1:已知点A(1,3),B(3,1),C(-1,0),求△ABC的面积
x
y
O
A
B
C
解:设AB边上的高为h
AB
=
(3-1)2+(1-3)2
=2
kAB=-1
AB的直线方程为:x+y-4=0
h=
-1+0-4
S= × × =5
1
2
2
5
还有其他的方法吗?
例2:用解析法证明:等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。
O
A(a,0)
C(-a,0)
B(0,b)
x
y
E
F
P
证明:建立如图直角坐标系,设P (x,0),x∈(-a,a )
lAB:bx+ay-ab=0, lCB: bx-ay+ab=0.
|PE|=
|bx-ab|
|PF|=
|bx+ab|
A到BC的距离h=
2ab
因为|PE|+|PF|=h,所以原命题得证。
例3.已知直线l经过点M(-1,2),且A(2,3),B(-4,5)两点到直线l的距离相等,求直线l的方程.
(方法一)当过点M(-1,2)的直线l的斜率不存在时,直线l的方程为x=-1,
恰好A(2,3),B(-4,5)两点到直线l的距离相等,故x=-1满足题意;
当过点M(-1,2)的直线l的斜率存在时,设l的方程为y-2=k(x+1),即kx-y+k+2=0,由A(2,3)与B(-4,5)两点到直线l的距离相等,得
k2+1
|2k-3+k+2|
=
|-4k-5+k+2|
k2+1
k=-
1
3
此时l的方程为y-2=- (x+1)
1
3
即x+3y-5=0.
综上所述,直线l的方程为x=-1
或x+3y-5=0.
(方法二)由题意得l∥AB或l过AB的中点.
当l∥AB时,设直线AB的斜率为kAB,
kAB=
-
1
3
l的方程为x+3y-5=0.
当l过AB的中点(-1,4)时,直线l的方程为x=-1.
综上所述,直线l的方程为x=-1或x+3y-5=0.
2.两条平行直线的距离
求两条平行直线Ax+By+C1=0与Ax+By+C2=0的距离.
x
y
o
l1
l2
P
Q
解:在直线上Ax+By+C1=0任取一点,如P(x0,y0)
则两平行线的距离就是点P(x0, y0)
到直线Ax+By+C2=0 的距离。(如图)
因此,d=
注意
(1)把直线方程化为直线的一般式方程;
(2)两条直线方程中x,y的系数必须分别相等;
(3)两平行线间的距离是一条直线上任一点到另一条直线的距离,也可以看作是两条直线上各取一点的最短距离.
(1)两直线变形为3x-2y-12=0与3x-2y+2=0,d=
(2)由题意得3×(-8)-(-4)×a=0.所以a=6.
c=-28或32.
求与两条平行直线l1:2x-3y+4=0或l2:2x-3y-2=0距离相等的直线l的方程.
设所求直线l的方程为2x-3y+C=0.
由直线l与两条平行线的距离相等,
即|C-4|=|C+2|,解得C=1.
故直线l的方程为2x-3y+1=0.
