2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.4.1圆的标准方程课件(16张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.4.1圆的标准方程课件(16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
2.4.1圆的标准方程
新课程标准解读 核心素养
1.掌握圆的定义及其标准方程.
2.会用待定系数法求圆的标准方程,判断点与圆的位置关系.
1.会用定义推导圆的标准方程,并掌握圆的标准方程的特征.(数学抽象)
2.能根据所给条件求圆的标准方程.(数学运算)
3.掌握点与圆的位置关系并能解决相关问题.(数学运算)
情境导入
月亮,是中国人心目中的宇宙精灵,古代人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写、吟咏月亮.有诗道:“明月四时有,何事喜中秋?瑶台宝鉴,宜挂玉宇最高头;放出白豪千丈,散作太虚一色.万象入吾眸,星斗避光彩,风露助清幽.”
如果把天空看作一个平面,在上面建立一个平面直角坐标系,那么月亮的坐标方程如何表示?
问题1:什么是圆?初中时我们是怎样给圆下定义的?
平面内与定点距离等于定长的点的集合(轨迹)是圆,定点就是圆心,定长就是半径.
问题2:平面直角坐标系中,如何确定一个圆?
确定圆的几何要素:圆心和半径
圆心:确定圆的位置
半径:确定圆的大小
问题3:圆心是A(a,b),半径是r的圆的方程是什么?
x
y
O
r
A(a,b)
M(x,y)
设点M (x,y)为圆A上任一点,则|MA|= r.
圆上所有点的集合P = { M | |MA| = r }
(x-a)2+(y-b)2=r2
点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.
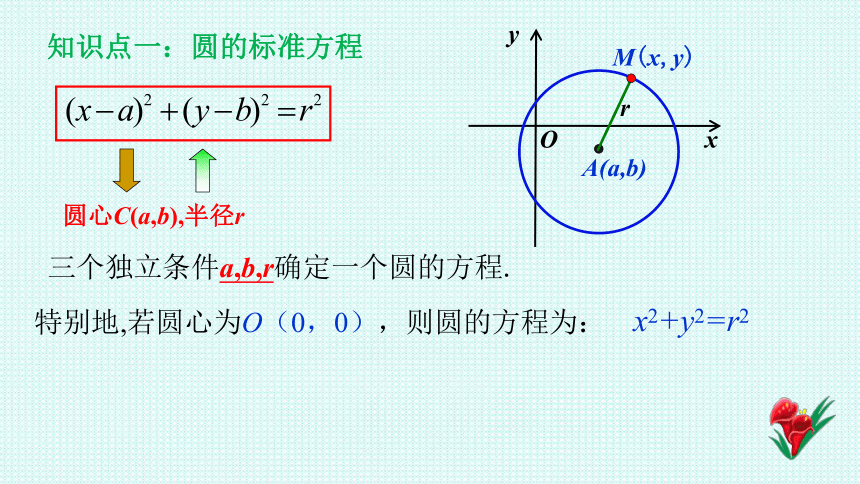
知识点一:圆的标准方程
圆心C(a,b),半径r
x
y
O
r
M(x,y)
A(a,b)
三个独立条件a,b,r确定一个圆的方程.
特别地,若圆心为O(0,0),则圆的方程为:
x2+y2=r2
1.判断正误.(正确的画“√”,错误的画“×”)
(1)方程(x-a)2+(y-b)2=m2一定表示圆. ( )
(2)若圆的标准方程为(x+m)2+(y+n)2=a2(a≠0),此圆的半径一定是a. ( )
2.给定圆的方程:(x-2)2+(y+8)2=9,则过坐标原点和圆心的直线方程为 ( )
A.4x-y=0 B.4x+y=0
C.x-4y=0 D.x+4y=0
由圆的标准方程,知圆心为(2,-8),则过坐标原点和圆心的直线方程为y=-4x,即4x+y=0.
知识点二:点与圆的位置关系
1.点M在圆外,|MC|>r
M(x,y)
C
(x0-a)2+(y0-b)2>r2时,点M在圆C外;
2.点M在圆上,|MC|=r
(x0-a)2+(y0-b)2=r2时,点M在圆C上;
C
M(x,y)
3.点M在圆内,|MC|(x0-a)2+(y0-b)2C
M(x,y)
1.点P(-2,-2)和圆x2+y2=4的位置关系是( )
A.在圆上 B.在圆外 C.在圆内 D.以上都不对
解析:将点P的坐标代入圆的方程,则(-2)2+(-2)2=8>4,故点P在圆外.
题型一
求圆的标准方程
方法1:设点C为圆心,∵点C在直线:x-2y-3=0上,
∴可设点C的坐标为(2a+3,a).又∵该圆经过A,B两点,∴|CA|=|CB|.
( )
( )
( )
( )
例1求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆
的标准方程.
解得a=-2.
故所求圆的标准方程为(x+1)2+(y+2)2=10.
方法2:设所求圆的标准方程为(x-a)2+(y-b)2=r2,圆心坐标为(a,b),
由条件知
( )
( )
( )
( )
故所求圆的标准方程为(x+1)2+(y+2)2=10.
方法3:线段AB的中点为(0,-4),
( )
( )
所以弦AB的垂直平分线的斜率k=-2,
所以线段AB的垂直平分线的方程为:y+4=-2x,即y=-2x-4.
圆心为(-1,-2),
故所求圆的标准方程为(x+1)2+(y+2)2=10.
圆的标准方程的两种求法
(1)几何法 它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
题型二
点和圆的位置关系
例2已知圆N的标准方程为(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆上,求a的值;
(2)已知点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,求a的取值范围.
(1)因为点M在圆上,所以(6-5)2+(9-6)2=a2,又a>0,可得
(2)由两点间距离公式可得,
=3.
因为线段PQ(不含端点)与圆有且只有一个公共点,即P,Q两点一个在圆N内,另一个在圆N外,
已知M(2,0),N(10,0),P(11,3),Q(6,1)四点,试判断它们是否共圆,并说明理由.
设M,N,P三点确定的圆的标准方程为(x-a)2+(y-b)2=r2,
∴过点M,N,P的圆的方程为(x-6)2+(y-3)2=25.
将点Q的坐标(6,1)代入方程左端,得(6-6)2+(1-3)2=4<25,
∴点Q不在圆(x-6)2+(y-3)2=25上,
∴M,N,P,Q四点不共圆.
题型三
与圆有关的最值问题
原方程表示以点(2,0)为圆心,
即y=kx,
当直线y=kx与圆相切时,斜率k取最大值和最小值,
o
x
y
1.(变设问)在本例条件下,求y-x的最大值和最小值.
设y-x=b,即y=x+b,当y=x+b与圆相切时,纵截距b取得最大值和最小值,
2.(变设问)在本例条件下,求x2+y2的最大值和最小值.
x2+y2表示圆上的点与原点距离的平方,由平面几何知识知,它在原点与圆心所在直线与圆的两个交点处取得最大值和最小值,又圆心到原点的距离为2,
2.4.1圆的标准方程
新课程标准解读 核心素养
1.掌握圆的定义及其标准方程.
2.会用待定系数法求圆的标准方程,判断点与圆的位置关系.
1.会用定义推导圆的标准方程,并掌握圆的标准方程的特征.(数学抽象)
2.能根据所给条件求圆的标准方程.(数学运算)
3.掌握点与圆的位置关系并能解决相关问题.(数学运算)
情境导入
月亮,是中国人心目中的宇宙精灵,古代人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写、吟咏月亮.有诗道:“明月四时有,何事喜中秋?瑶台宝鉴,宜挂玉宇最高头;放出白豪千丈,散作太虚一色.万象入吾眸,星斗避光彩,风露助清幽.”
如果把天空看作一个平面,在上面建立一个平面直角坐标系,那么月亮的坐标方程如何表示?
问题1:什么是圆?初中时我们是怎样给圆下定义的?
平面内与定点距离等于定长的点的集合(轨迹)是圆,定点就是圆心,定长就是半径.
问题2:平面直角坐标系中,如何确定一个圆?
确定圆的几何要素:圆心和半径
圆心:确定圆的位置
半径:确定圆的大小
问题3:圆心是A(a,b),半径是r的圆的方程是什么?
x
y
O
r
A(a,b)
M(x,y)
设点M (x,y)为圆A上任一点,则|MA|= r.
圆上所有点的集合P = { M | |MA| = r }
(x-a)2+(y-b)2=r2
点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.
知识点一:圆的标准方程
圆心C(a,b),半径r
x
y
O
r
M(x,y)
A(a,b)
三个独立条件a,b,r确定一个圆的方程.
特别地,若圆心为O(0,0),则圆的方程为:
x2+y2=r2
1.判断正误.(正确的画“√”,错误的画“×”)
(1)方程(x-a)2+(y-b)2=m2一定表示圆. ( )
(2)若圆的标准方程为(x+m)2+(y+n)2=a2(a≠0),此圆的半径一定是a. ( )
2.给定圆的方程:(x-2)2+(y+8)2=9,则过坐标原点和圆心的直线方程为 ( )
A.4x-y=0 B.4x+y=0
C.x-4y=0 D.x+4y=0
由圆的标准方程,知圆心为(2,-8),则过坐标原点和圆心的直线方程为y=-4x,即4x+y=0.
知识点二:点与圆的位置关系
1.点M在圆外,|MC|>r
M(x,y)
C
(x0-a)2+(y0-b)2>r2时,点M在圆C外;
2.点M在圆上,|MC|=r
(x0-a)2+(y0-b)2=r2时,点M在圆C上;
C
M(x,y)
3.点M在圆内,|MC|
M(x,y)
1.点P(-2,-2)和圆x2+y2=4的位置关系是( )
A.在圆上 B.在圆外 C.在圆内 D.以上都不对
解析:将点P的坐标代入圆的方程,则(-2)2+(-2)2=8>4,故点P在圆外.
题型一
求圆的标准方程
方法1:设点C为圆心,∵点C在直线:x-2y-3=0上,
∴可设点C的坐标为(2a+3,a).又∵该圆经过A,B两点,∴|CA|=|CB|.
( )
( )
( )
( )
例1求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆
的标准方程.
解得a=-2.
故所求圆的标准方程为(x+1)2+(y+2)2=10.
方法2:设所求圆的标准方程为(x-a)2+(y-b)2=r2,圆心坐标为(a,b),
由条件知
( )
( )
( )
( )
故所求圆的标准方程为(x+1)2+(y+2)2=10.
方法3:线段AB的中点为(0,-4),
( )
( )
所以弦AB的垂直平分线的斜率k=-2,
所以线段AB的垂直平分线的方程为:y+4=-2x,即y=-2x-4.
圆心为(-1,-2),
故所求圆的标准方程为(x+1)2+(y+2)2=10.
圆的标准方程的两种求法
(1)几何法 它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
题型二
点和圆的位置关系
例2已知圆N的标准方程为(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆上,求a的值;
(2)已知点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,求a的取值范围.
(1)因为点M在圆上,所以(6-5)2+(9-6)2=a2,又a>0,可得
(2)由两点间距离公式可得,
=3.
因为线段PQ(不含端点)与圆有且只有一个公共点,即P,Q两点一个在圆N内,另一个在圆N外,
已知M(2,0),N(10,0),P(11,3),Q(6,1)四点,试判断它们是否共圆,并说明理由.
设M,N,P三点确定的圆的标准方程为(x-a)2+(y-b)2=r2,
∴过点M,N,P的圆的方程为(x-6)2+(y-3)2=25.
将点Q的坐标(6,1)代入方程左端,得(6-6)2+(1-3)2=4<25,
∴点Q不在圆(x-6)2+(y-3)2=25上,
∴M,N,P,Q四点不共圆.
题型三
与圆有关的最值问题
原方程表示以点(2,0)为圆心,
即y=kx,
当直线y=kx与圆相切时,斜率k取最大值和最小值,
o
x
y
1.(变设问)在本例条件下,求y-x的最大值和最小值.
设y-x=b,即y=x+b,当y=x+b与圆相切时,纵截距b取得最大值和最小值,
2.(变设问)在本例条件下,求x2+y2的最大值和最小值.
x2+y2表示圆上的点与原点距离的平方,由平面几何知识知,它在原点与圆心所在直线与圆的两个交点处取得最大值和最小值,又圆心到原点的距离为2,
