2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.5.1直线和圆的位置关系第二课时课件(16张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.5.1直线和圆的位置关系第二课时课件(16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 12:34:33 | ||
图片预览






文档简介
(共16张PPT)
2.5.1直线和圆的位置关系
第二课时
题型一
直线与圆的方程实际应用
例1.已知台风中心从A地以20 km/h的速度向东北方向移动,离台风中心30 km内的地区为危险区,城市B在A的正东40 km处,求B城市处于危险区内的时间.
【解】如图,以A为原点,以AB所在直线为x轴建立平面直角坐标系.
射线AC为∠xAy的平分线,则台风中心在射线AC上移动,点B到AC的距离为
.
x
y
C
A
B
则射线AC被以B为圆心,以30 km为半径的圆截得的弦长为
所以B城市处于危险区内的时间为t=1(h).
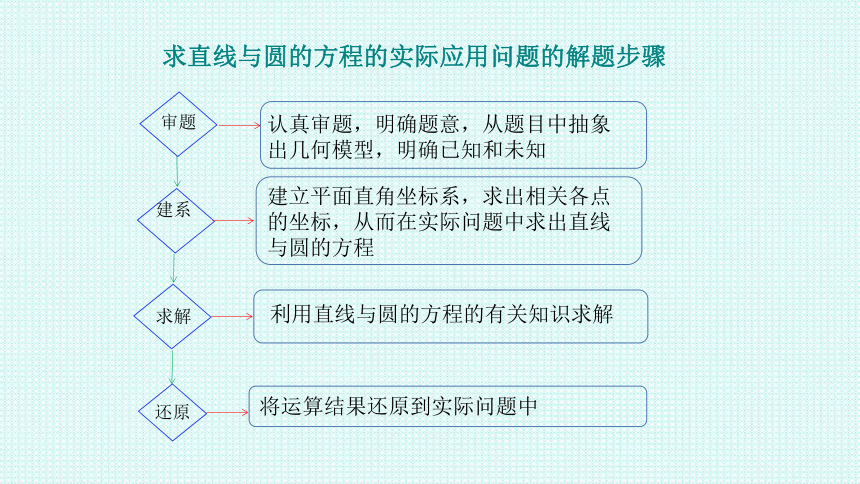
审题
认真审题,明确题意,从题目中抽象出几何模型,明确已知和未知
建系
利用直线与圆的方程的有关知识求解
求解
还原
将运算结果还原到实际问题中
建立平面直角坐标系,求出相关各点的坐标,从而在实际问题中求出直线与圆的方程
求直线与圆的方程的实际应用问题的解题步骤
已知隧道的截面是半径为4.0 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m、高为2.5 m的货车能不能驶入这个隧道?假设货车的最大宽度为2 m,那么要正常驶入该隧道,货车的最大高度为多少?
解:以隧道截面半圆的圆心为坐标原点,半圆直径所在直线为x轴,
建立如图所示的平面直角坐标系,则半圆方程为x2+y2=16(y≥0).
o
x
y
2.7
4
将x=2.7代入x2+y2=16(y≥0),得y=
即在离中心线2.7 m处,隧道高度高于货车的高度,
所以货车能驶入这个隧道.
将x=2代入x2+y2=16(y≥0),得
所以货车要驶入该隧道,
题型二
与圆有关的最值问题
例2 已知实数x,y满足方程x2+y2-4x+1=0.
(2)求y-x的最大值和最小值.
解:原方程可化为(x-2)2+y2=3,表示以(2,0)为圆心,
的几何意义是圆上一点与原点连线的的斜率,
即y=kx.
o
x
y
当直线y=kx与圆相切时,斜率k取
得最大值或最小值,
(2)y-x可看作是直线y=x+b在y轴上的截距,
当直线y=x+b与圆相切时,b取得最大值或最小值,
o
x
y
在本例条件下,求x2+y2的最大值和最小值.
解:x2+y2表示圆上的一点与原点距离的平方,
又圆心到原点的距离为
所以x2+y2的最大值是
x2+y2的最小值是
设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为( )
A.6 B.4 C.3 D.2
解析:画出已知图,利用数形结合的思想求解.如图,圆心M(3,-1)与定直线x=-3的最短距离为|MQ|=3-(-3)=6.因为圆的半径为2,所以|PQ|的最小值为6-2=4.
o
x
y
Q
x=-3
M
题型三
过直线与圆的交点的圆系方程
例3.已知圆C经过直线x+y+2=0与圆x2+y2=4的交点,且圆C的圆心在直线2x-y-3=0上,求圆C的方程.
设所求圆的方程为(x2+y2-4)+a(x+y+2)=0,
即x2+y2+ax+ay-4+2a=0,
因为圆心在直线2x-y-3=0上,
所以a=-6.
所以圆的方程为x2+y2-6x-6y-16=0,
即(x-3)2+(y-3)2=34.
求过直线与圆的交点的圆系方程的方法
(1)联立方程组,求出交点坐标,再根据交点坐标求方程;
(2)设圆系方程求参数,一般地,过直线l:Ax+By+C=0与圆O:x2+y2+Dx+Ey+F=0(D2+E2-4F>0)的交点的圆系方程可设为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0.
求经过直线x+y=0与圆x2+y2+2x-4y-8=0的交点,且经过点P(-1,-2)的圆的方程.
解方程组
所以直线与圆交于点A(1,-1)和点B(-4,4).
设所求圆的方程为x2+y2+Dx+Ey+F=0(D2+E2-4F>0),
故所求圆的方程为x2+y2+3x-3y-8=0.
方法二:设所求圆的方程为x2+y2+2x-4y-8+λ(x+y)=0,
又点P(-1,-2)在圆上,将(-1,-2)代入圆的方程得(-1)2+(-2)2+2×(-1)-4×(-2)-8+λ(-1-2)=0,解得λ=1.
故所求圆的方程为x2+y2+2x-4y-8+x+y=0,
即x2+y2+3x-3y-8=0.
1.已知圆x2+y2+2x+2y+k=0和定点P(1,-1),若过点P的圆的切线有两条,则k的取值范围是 ( )
A.(-2,+∞) B.(-∞,2)
C.(-2,2) D.(-∞,-2)∪(2,+∞)
由题意知点P(1,-1)必须在圆的外部,
则12+(-1)2+2×1+2×(-1)+k>0,解得k>-2.
2.设某村庄外围成圆形,其所在曲线的方程可用(x-2)2+(y+3)2=4表示,村外一小路方程可用x-y+2=0表示,则从村庄外围到小路的最短距离是________.
圆心(2,-3)到直线x-y+2=0的距离减去圆的半径2,
3
直线y=kx与圆(x-2)2+y2=1的两个交点关于直线2x+y+b=0对称,则y=kx与
直线2x+y+b=0垂直,且2x+y+b=0过圆心,k= ,b=-4
1
2
o
x
y
4
x
y
O
当直线经过点(0,1)时,直线与圆有两个不同的交点,m=1,当直线与圆相切时,
3
2
m=
5.过点(3,1)作圆(x-2)2+(y-2)2=4的弦,其中最短弦的长为______.
最短弦为过点(3,1),且垂直于点(3,1)与圆心的连线的弦
x
y
O
(2)2-( )2
2
=2
2.5.1直线和圆的位置关系
第二课时
题型一
直线与圆的方程实际应用
例1.已知台风中心从A地以20 km/h的速度向东北方向移动,离台风中心30 km内的地区为危险区,城市B在A的正东40 km处,求B城市处于危险区内的时间.
【解】如图,以A为原点,以AB所在直线为x轴建立平面直角坐标系.
射线AC为∠xAy的平分线,则台风中心在射线AC上移动,点B到AC的距离为
.
x
y
C
A
B
则射线AC被以B为圆心,以30 km为半径的圆截得的弦长为
所以B城市处于危险区内的时间为t=1(h).
审题
认真审题,明确题意,从题目中抽象出几何模型,明确已知和未知
建系
利用直线与圆的方程的有关知识求解
求解
还原
将运算结果还原到实际问题中
建立平面直角坐标系,求出相关各点的坐标,从而在实际问题中求出直线与圆的方程
求直线与圆的方程的实际应用问题的解题步骤
已知隧道的截面是半径为4.0 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m、高为2.5 m的货车能不能驶入这个隧道?假设货车的最大宽度为2 m,那么要正常驶入该隧道,货车的最大高度为多少?
解:以隧道截面半圆的圆心为坐标原点,半圆直径所在直线为x轴,
建立如图所示的平面直角坐标系,则半圆方程为x2+y2=16(y≥0).
o
x
y
2.7
4
将x=2.7代入x2+y2=16(y≥0),得y=
即在离中心线2.7 m处,隧道高度高于货车的高度,
所以货车能驶入这个隧道.
将x=2代入x2+y2=16(y≥0),得
所以货车要驶入该隧道,
题型二
与圆有关的最值问题
例2 已知实数x,y满足方程x2+y2-4x+1=0.
(2)求y-x的最大值和最小值.
解:原方程可化为(x-2)2+y2=3,表示以(2,0)为圆心,
的几何意义是圆上一点与原点连线的的斜率,
即y=kx.
o
x
y
当直线y=kx与圆相切时,斜率k取
得最大值或最小值,
(2)y-x可看作是直线y=x+b在y轴上的截距,
当直线y=x+b与圆相切时,b取得最大值或最小值,
o
x
y
在本例条件下,求x2+y2的最大值和最小值.
解:x2+y2表示圆上的一点与原点距离的平方,
又圆心到原点的距离为
所以x2+y2的最大值是
x2+y2的最小值是
设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为( )
A.6 B.4 C.3 D.2
解析:画出已知图,利用数形结合的思想求解.如图,圆心M(3,-1)与定直线x=-3的最短距离为|MQ|=3-(-3)=6.因为圆的半径为2,所以|PQ|的最小值为6-2=4.
o
x
y
Q
x=-3
M
题型三
过直线与圆的交点的圆系方程
例3.已知圆C经过直线x+y+2=0与圆x2+y2=4的交点,且圆C的圆心在直线2x-y-3=0上,求圆C的方程.
设所求圆的方程为(x2+y2-4)+a(x+y+2)=0,
即x2+y2+ax+ay-4+2a=0,
因为圆心在直线2x-y-3=0上,
所以a=-6.
所以圆的方程为x2+y2-6x-6y-16=0,
即(x-3)2+(y-3)2=34.
求过直线与圆的交点的圆系方程的方法
(1)联立方程组,求出交点坐标,再根据交点坐标求方程;
(2)设圆系方程求参数,一般地,过直线l:Ax+By+C=0与圆O:x2+y2+Dx+Ey+F=0(D2+E2-4F>0)的交点的圆系方程可设为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0.
求经过直线x+y=0与圆x2+y2+2x-4y-8=0的交点,且经过点P(-1,-2)的圆的方程.
解方程组
所以直线与圆交于点A(1,-1)和点B(-4,4).
设所求圆的方程为x2+y2+Dx+Ey+F=0(D2+E2-4F>0),
故所求圆的方程为x2+y2+3x-3y-8=0.
方法二:设所求圆的方程为x2+y2+2x-4y-8+λ(x+y)=0,
又点P(-1,-2)在圆上,将(-1,-2)代入圆的方程得(-1)2+(-2)2+2×(-1)-4×(-2)-8+λ(-1-2)=0,解得λ=1.
故所求圆的方程为x2+y2+2x-4y-8+x+y=0,
即x2+y2+3x-3y-8=0.
1.已知圆x2+y2+2x+2y+k=0和定点P(1,-1),若过点P的圆的切线有两条,则k的取值范围是 ( )
A.(-2,+∞) B.(-∞,2)
C.(-2,2) D.(-∞,-2)∪(2,+∞)
由题意知点P(1,-1)必须在圆的外部,
则12+(-1)2+2×1+2×(-1)+k>0,解得k>-2.
2.设某村庄外围成圆形,其所在曲线的方程可用(x-2)2+(y+3)2=4表示,村外一小路方程可用x-y+2=0表示,则从村庄外围到小路的最短距离是________.
圆心(2,-3)到直线x-y+2=0的距离减去圆的半径2,
3
直线y=kx与圆(x-2)2+y2=1的两个交点关于直线2x+y+b=0对称,则y=kx与
直线2x+y+b=0垂直,且2x+y+b=0过圆心,k= ,b=-4
1
2
o
x
y
4
x
y
O
当直线经过点(0,1)时,直线与圆有两个不同的交点,m=1,当直线与圆相切时,
3
2
m=
5.过点(3,1)作圆(x-2)2+(y-2)2=4的弦,其中最短弦的长为______.
最短弦为过点(3,1),且垂直于点(3,1)与圆心的连线的弦
x
y
O
(2)2-( )2
2
=2
