2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.5.1直线和圆的位置关系第一课时课件(16张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.5.1直线和圆的位置关系第一课时课件(16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
2.5.1直线和圆的位置关系
第一课时
新课程标准解读 核心素养
1.掌握直线与圆的三种位置关系.
2.会用代数法和几何法来判断直线与圆的三种位置关系.
3.理解并掌握直线与圆的方程在实际生活中的应用. 1.能根据给定直线、圆的方程,判断直线与圆的位置关系.(逻辑推理)
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.(数学建模)
情境导学
“大漠孤烟直,长河落日圆”,这是唐代诗人王维的诗句.它描述了黄昏日落时分塞外特有的景象.
从日落这种自然现象中可以抽象出哪些基本的几何图形呢?它们有哪些位置关系呢?
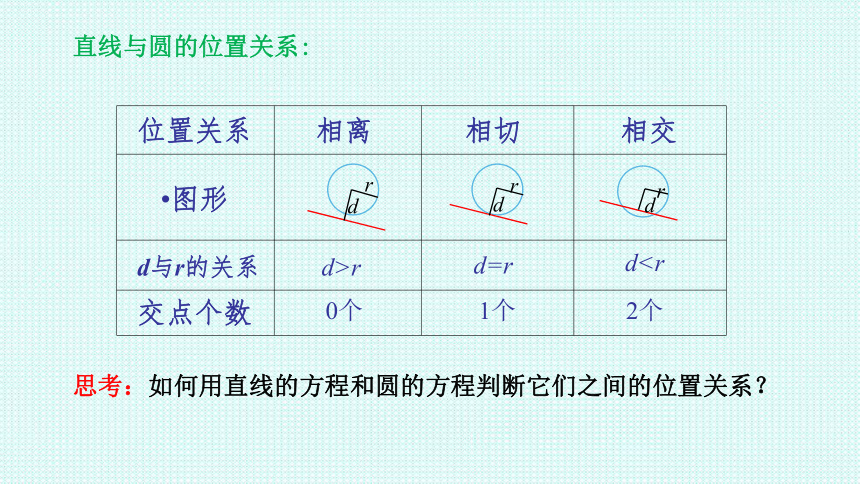
直线与圆的位置关系:
位置关系
相离
相切
相交
图形
d与r的关系
交点个数
r
d
d>r
0个
r
d
d=r
1个
r
d
d2个
思考:如何用直线的方程和圆的方程判断它们之间的位置关系?
例1.如图,已知直线l:3x+y-6=0 和圆心为C的圆 x2+y2-2y-4=0 ,判断直线 l 与圆的位置关系;
.
x
y
O
C
A
B
l
解法一:由直线与圆的方程,得
所以直线与圆相交,有两个公共点.
所以直线与圆有两个交点,坐标分别为A(2,0),B(1,3)
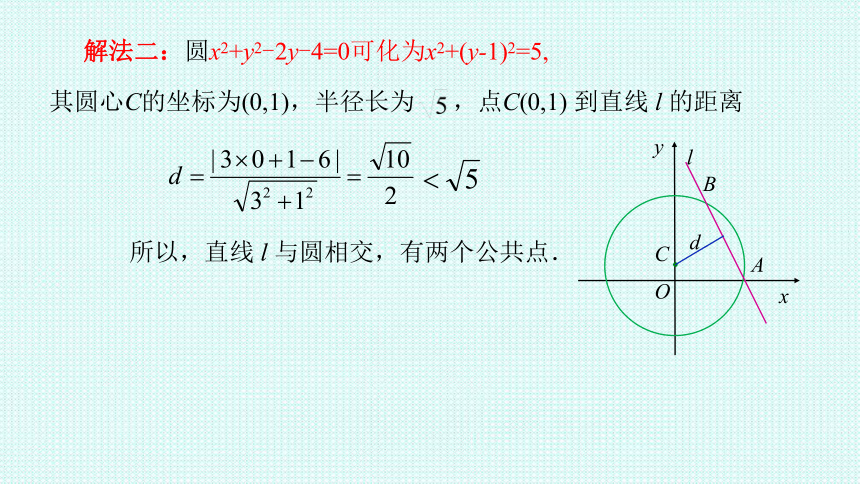
解法二:圆x2+y2-2y-4=0可化为x2+(y-1)2=5,
其圆心C的坐标为(0,1),半径长为 ,点C(0,1) 到直线 l 的距离
所以,直线 l 与圆相交,有两个公共点.
.
x
y
O
C
A
B
l
d
一、直线与圆的位置关系的判定方法:
(1)利用直线与圆的交点的个数进行判断:
△<0
直线与圆相离
△=0
△>0
直线与圆相切
直线与圆相交
(2)利用圆心到直线的距离d与半径r的大小关系判断:
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
“几何法”侧重于图形的几何性质,步骤较简洁;“代数法”则侧重于“坐标”与“方程”,判断直线与圆的位置关系,一般用几何法.
题型一
直线和圆的位置关系判断
例2.已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,直线与圆
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点?
方法1:将直线mx-y-m-1=0代入圆的方程,化简、整理,得(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.∵Δ=4m(3m+4),
直线与圆相交,即直线与圆有两个公共点;
直线与圆相切,即直线与圆只有一个公共点;
直线与圆相离,即直线与圆没有公共点.
[规律方法] 直线与圆的位置关系的判断方法
直线与圆的位置关系反映在三个方面:一是点到直线的距离与半径大小的关系;二是直线与圆的公共点的个数;三是两方程组成的方程组解的个数.因此,若给出图形,可根据公共点的个数判断;若给出直线与圆的方程,可选择用几何法或代数法,几何法计算量小,代数法可一同求出交点.解题时可根据条件作出恰当的选择.
1.直线x-ky+1=0与圆x2+y2=1的位置关系是 ( )
A.相交 B.相离
C.相交或相切 D.相切
解析:直线x-ky+1=0恒过定点(-1,0),而(-1,0)在圆上,故直线与圆相切或相交.
2.已知点(a,b)在圆C:x2+y2=r2(r≠0)的外部,则直线ax+by=r2与C的位置关系是 ( )
A.相切 B.相离
C.相交 D.不确定
解析:由已知a2+b2>r2,且圆心到直线ax+by=r2的距离为
则d<r,故直线ax+by=r2与圆C的位置关系是相交.
题型二
直线和圆相切
[例3](1)设直线mx-y+2=0与圆x2+y2=1相切,则m=________;
(2)过点A(-1,4)作圆(x-2)2+(y-3)2=1的切线l,求切线l的方程为_____.
[解析] (1)已知圆的圆心为O(0,0),半径r=1,则O到已知直线的距离
(2)∵(-1-2)2+(4-3)2=10>1,∴点A在圆外.
当直线l的斜率不存在时,l的方程是x=-1,不满足题意.
设直线l的斜率为k,则切线l的方程为y-4=k(x+1),
即kx-y+4+k=0.圆心(2,3)到切线l的距离为
直线l的方程y=4或3x+4y-13=0.
.
x
y
O
A
题型三
弦长问题
[解] 圆x2+y2=25的半径长r为5,直线被圆所截得的弦长l=8,于是弦心距d=
因为圆心O(0,0)到直线x=-3的距离恰为3,所以直线x=-3是符合题意的一条直线.
当直线的斜率存在时,
=3,
对应的方程分别为x=-3或3x+4y+15=0.
例5.已知圆的方程为x2+y2=8,圆内有一点P(-1,2),AB为过点P且倾斜角为α的弦.
(1)当α=135°时,求AB的长;
(2)当弦AB被点P平分时,求直线AB的方程.
x
y
O
【解】 (1)方法一(几何法):如图所示,过点O作OC⊥AB.
由已知条件得直线的斜率为k=tan 135°=-1,
所以直线AB的方程为y-2=-(x+1),即x+y-1=0.
C
因为圆心为(0,0),所以|OC|
B
A
P
方法二(代数法):当α=135°时,直线AB的方程为y-2=-(x+1),
即y=-x+1,代入x2+y2=8,得2x2-2x-7=0.
(2)如图,当弦AB被点P平分时,OP⊥AB,因为kOP=-2,
所以直线AB的方程为y-2=
即x-2y+5=0.
x
y
O
P
A
B
2.5.1直线和圆的位置关系
第一课时
新课程标准解读 核心素养
1.掌握直线与圆的三种位置关系.
2.会用代数法和几何法来判断直线与圆的三种位置关系.
3.理解并掌握直线与圆的方程在实际生活中的应用. 1.能根据给定直线、圆的方程,判断直线与圆的位置关系.(逻辑推理)
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.(数学建模)
情境导学
“大漠孤烟直,长河落日圆”,这是唐代诗人王维的诗句.它描述了黄昏日落时分塞外特有的景象.
从日落这种自然现象中可以抽象出哪些基本的几何图形呢?它们有哪些位置关系呢?
直线与圆的位置关系:
位置关系
相离
相切
相交
图形
d与r的关系
交点个数
r
d
d>r
0个
r
d
d=r
1个
r
d
d
思考:如何用直线的方程和圆的方程判断它们之间的位置关系?
例1.如图,已知直线l:3x+y-6=0 和圆心为C的圆 x2+y2-2y-4=0 ,判断直线 l 与圆的位置关系;
.
x
y
O
C
A
B
l
解法一:由直线与圆的方程,得
所以直线与圆相交,有两个公共点.
所以直线与圆有两个交点,坐标分别为A(2,0),B(1,3)
解法二:圆x2+y2-2y-4=0可化为x2+(y-1)2=5,
其圆心C的坐标为(0,1),半径长为 ,点C(0,1) 到直线 l 的距离
所以,直线 l 与圆相交,有两个公共点.
.
x
y
O
C
A
B
l
d
一、直线与圆的位置关系的判定方法:
(1)利用直线与圆的交点的个数进行判断:
△<0
直线与圆相离
△=0
△>0
直线与圆相切
直线与圆相交
(2)利用圆心到直线的距离d与半径r的大小关系判断:
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
“几何法”侧重于图形的几何性质,步骤较简洁;“代数法”则侧重于“坐标”与“方程”,判断直线与圆的位置关系,一般用几何法.
题型一
直线和圆的位置关系判断
例2.已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,直线与圆
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点?
方法1:将直线mx-y-m-1=0代入圆的方程,化简、整理,得(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.∵Δ=4m(3m+4),
直线与圆相交,即直线与圆有两个公共点;
直线与圆相切,即直线与圆只有一个公共点;
直线与圆相离,即直线与圆没有公共点.
[规律方法] 直线与圆的位置关系的判断方法
直线与圆的位置关系反映在三个方面:一是点到直线的距离与半径大小的关系;二是直线与圆的公共点的个数;三是两方程组成的方程组解的个数.因此,若给出图形,可根据公共点的个数判断;若给出直线与圆的方程,可选择用几何法或代数法,几何法计算量小,代数法可一同求出交点.解题时可根据条件作出恰当的选择.
1.直线x-ky+1=0与圆x2+y2=1的位置关系是 ( )
A.相交 B.相离
C.相交或相切 D.相切
解析:直线x-ky+1=0恒过定点(-1,0),而(-1,0)在圆上,故直线与圆相切或相交.
2.已知点(a,b)在圆C:x2+y2=r2(r≠0)的外部,则直线ax+by=r2与C的位置关系是 ( )
A.相切 B.相离
C.相交 D.不确定
解析:由已知a2+b2>r2,且圆心到直线ax+by=r2的距离为
则d<r,故直线ax+by=r2与圆C的位置关系是相交.
题型二
直线和圆相切
[例3](1)设直线mx-y+2=0与圆x2+y2=1相切,则m=________;
(2)过点A(-1,4)作圆(x-2)2+(y-3)2=1的切线l,求切线l的方程为_____.
[解析] (1)已知圆的圆心为O(0,0),半径r=1,则O到已知直线的距离
(2)∵(-1-2)2+(4-3)2=10>1,∴点A在圆外.
当直线l的斜率不存在时,l的方程是x=-1,不满足题意.
设直线l的斜率为k,则切线l的方程为y-4=k(x+1),
即kx-y+4+k=0.圆心(2,3)到切线l的距离为
直线l的方程y=4或3x+4y-13=0.
.
x
y
O
A
题型三
弦长问题
[解] 圆x2+y2=25的半径长r为5,直线被圆所截得的弦长l=8,于是弦心距d=
因为圆心O(0,0)到直线x=-3的距离恰为3,所以直线x=-3是符合题意的一条直线.
当直线的斜率存在时,
=3,
对应的方程分别为x=-3或3x+4y+15=0.
例5.已知圆的方程为x2+y2=8,圆内有一点P(-1,2),AB为过点P且倾斜角为α的弦.
(1)当α=135°时,求AB的长;
(2)当弦AB被点P平分时,求直线AB的方程.
x
y
O
【解】 (1)方法一(几何法):如图所示,过点O作OC⊥AB.
由已知条件得直线的斜率为k=tan 135°=-1,
所以直线AB的方程为y-2=-(x+1),即x+y-1=0.
C
因为圆心为(0,0),所以|OC|
B
A
P
方法二(代数法):当α=135°时,直线AB的方程为y-2=-(x+1),
即y=-x+1,代入x2+y2=8,得2x2-2x-7=0.
(2)如图,当弦AB被点P平分时,OP⊥AB,因为kOP=-2,
所以直线AB的方程为y-2=
即x-2y+5=0.
x
y
O
P
A
B
