2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.1椭圆习题课课件(20张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.1椭圆习题课课件(20张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 12:41:31 | ||
图片预览








文档简介
(共20张PPT)
3.1椭圆的习题课
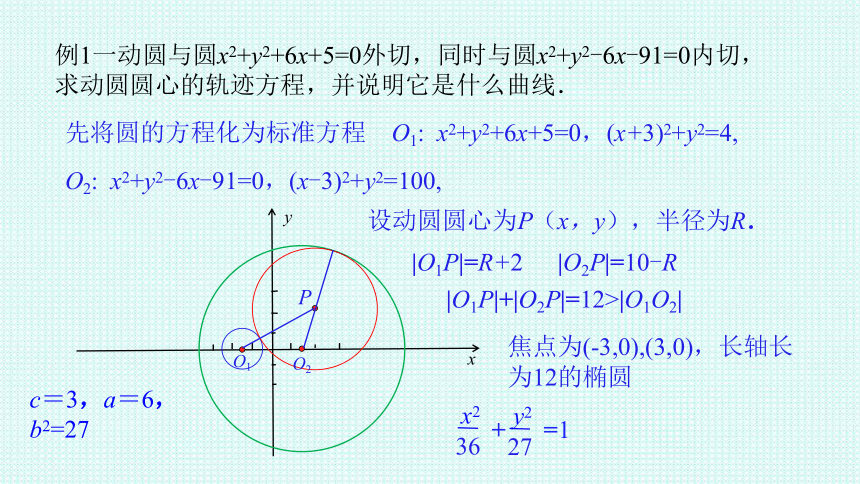
例1一动圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线.
先将圆的方程化为标准方程
O1: x2+y2+6x+5=0,(x+3)2+y2=4,
O2: x2+y2-6x-91=0,(x-3)2+y2=100,
x
y
O1
O2
设动圆圆心为P(x,y),半径为R.
P
|O1P|=R+2
|O2P|=10-R
|O1P|+|O2P|=12 |O1O2|
c=3,a=6,b2=27
x2
36
+ =1
y2
27
焦点为(-3,0),(3,0),长轴长为12的椭圆
例2.已知椭圆C:
内有一点M(2,3),F1,F2分别为椭圆
的左、右焦点,P为椭圆C上的一点,求:
(1)|PM|-|PF1|的最大值与最小值;
(2)|PM|+|PF1|的最大值与最小值.
x
y
O
F1
F2
M
P
由三边不等关系,当PM、PF1共线时,|PM|-|PF1|取最大为|MF1|,
P
|PM|-|PF1|=-(|PF1|-|PM|)
所以|PM|-|PF1|的最小值即是求|PF1|-|PM|最大值.
(2)|PM|+|PF1|=2a+|PM|-|PF2|=10+|PM|-|PF2|
|PM|-|PF2|的最大值为 ,最小值为-
(|PM|+|PF1|)max
已知点A(1,1),F1是椭圆
的左焦点,P是椭圆上任
意一点,求|PF1|+|PA|的最小值和最大值.
设椭圆的右焦点为F2,则F2(2,0).|PF1|+|PA|=2a-|PF2|+|PA|
=2a-(|PF2|-|PA|)
|PF1|+|PA|=2a-|PF2|+|PA|
x
y
O
F1
F2
设此椭圆的长半轴长为a,短半轴长为b,焦距为2c,则b=1,
b
a
所以椭圆的标准方程是
①对于焦点不清楚的要分两种情况;
②两端点的距离代表的是什么?
(2).在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为6,求椭圆的标准方程.
O
x
y
F
A1
A2
如图所示,△A1FA2为一等腰直角三角形,OF为斜边A1A2的中线(高),且|OF|=c,|A1A2|=2b,∴c=b=3,∴a2=b2+c2=18,
(3).已知中心在原点,焦点在x轴上的椭圆C上的点到焦点的距离的最大值为3,最小值为1,则椭圆C的标准方程为________.
O
x
y
F1
F2
b
c
a+c
a-c
最大值:a+c 最小值:a-c
必须将椭圆方程化为标准形式,才能正确找出a,b,并求出c
可以求e2,再开方,依据离心率的范围确定
x2+ =1
y2
1
4
c2
a2
e2=
分焦点在不同的轴上进行讨论,
若焦点在x轴上,则0若焦点在y轴上,则m 2,
a 0
O
x
y
F1
F2
A
B
x=c,y=±
b2
a
AB
=
2b2
a
=1
a=2,c=
O
x
y
F1
F2
P
P
a b 0
O
x
y
P
B2
F1
F2
∠F1B2F2≥∠F1PF2
O
B2
F2
b
c
a
c
a
≥sin300
由题意得F(-1,0),设点P(x0,y0),
OP·FP=x0(x0+1)+y02
y02=3(1- )
x02
4
(-2≤ x0 ≤2)
OP·FP= (x0+2)2+2
1
4
当x0=2时,OP·FP取得最大值为6
当P,Q分别在椭圆短轴端点时,四边形PF1QF2的面积最大.
O
x
y
F
B
M
N
设M(x1,y1),N(x2,y2),
a2
x12
y12
b2
+ =1,
y22
b2
x22
a2
+ =1
y1-y2
x1-x2
y1+y2
x1+x2
·
=-
a2
b2
x1+x2=4,y1+y2=-2,
a2=2bc=b2+c2
b=c,a+c=4+2
a=4
O
x
y
F
E
N
M
E点为椭圆的右焦点,|MF|+|ME|=6,则
|MF|=6-|ME|,
|MF|+|MN|=6-(|ME|-|MN|)
当M,E,N三点共线时,|ME|-|MN|最大值为1,|MF|+|MN|最小值为5
例6. 点 M(x, y) 与定点 F(4, 0) 的距离和它到直线 l: 距离的比是常数 求点 M 的轨迹.
设 M 到 l 的距离为 d, 则
|MF|
d
=
4
5
(x-4)2+y2
| - x|
25
4
4
5
=
化简得 9x2+25y2=225,
x2
25
+ =1
y2
9
O
x
y
F
M
定点是右焦点,定直线叫右准线, 比值是离心率.
a2
c
x=
O
x
y
F
B
A
3.1椭圆的习题课
例1一动圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线.
先将圆的方程化为标准方程
O1: x2+y2+6x+5=0,(x+3)2+y2=4,
O2: x2+y2-6x-91=0,(x-3)2+y2=100,
x
y
O1
O2
设动圆圆心为P(x,y),半径为R.
P
|O1P|=R+2
|O2P|=10-R
|O1P|+|O2P|=12 |O1O2|
c=3,a=6,b2=27
x2
36
+ =1
y2
27
焦点为(-3,0),(3,0),长轴长为12的椭圆
例2.已知椭圆C:
内有一点M(2,3),F1,F2分别为椭圆
的左、右焦点,P为椭圆C上的一点,求:
(1)|PM|-|PF1|的最大值与最小值;
(2)|PM|+|PF1|的最大值与最小值.
x
y
O
F1
F2
M
P
由三边不等关系,当PM、PF1共线时,|PM|-|PF1|取最大为|MF1|,
P
|PM|-|PF1|=-(|PF1|-|PM|)
所以|PM|-|PF1|的最小值即是求|PF1|-|PM|最大值.
(2)|PM|+|PF1|=2a+|PM|-|PF2|=10+|PM|-|PF2|
|PM|-|PF2|的最大值为 ,最小值为-
(|PM|+|PF1|)max
已知点A(1,1),F1是椭圆
的左焦点,P是椭圆上任
意一点,求|PF1|+|PA|的最小值和最大值.
设椭圆的右焦点为F2,则F2(2,0).|PF1|+|PA|=2a-|PF2|+|PA|
=2a-(|PF2|-|PA|)
|PF1|+|PA|=2a-|PF2|+|PA|
x
y
O
F1
F2
设此椭圆的长半轴长为a,短半轴长为b,焦距为2c,则b=1,
b
a
所以椭圆的标准方程是
①对于焦点不清楚的要分两种情况;
②两端点的距离代表的是什么?
(2).在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为6,求椭圆的标准方程.
O
x
y
F
A1
A2
如图所示,△A1FA2为一等腰直角三角形,OF为斜边A1A2的中线(高),且|OF|=c,|A1A2|=2b,∴c=b=3,∴a2=b2+c2=18,
(3).已知中心在原点,焦点在x轴上的椭圆C上的点到焦点的距离的最大值为3,最小值为1,则椭圆C的标准方程为________.
O
x
y
F1
F2
b
c
a+c
a-c
最大值:a+c 最小值:a-c
必须将椭圆方程化为标准形式,才能正确找出a,b,并求出c
可以求e2,再开方,依据离心率的范围确定
x2+ =1
y2
1
4
c2
a2
e2=
分焦点在不同的轴上进行讨论,
若焦点在x轴上,则0
a 0
O
x
y
F1
F2
A
B
x=c,y=±
b2
a
AB
=
2b2
a
=1
a=2,c=
O
x
y
F1
F2
P
P
a b 0
O
x
y
P
B2
F1
F2
∠F1B2F2≥∠F1PF2
O
B2
F2
b
c
a
c
a
≥sin300
由题意得F(-1,0),设点P(x0,y0),
OP·FP=x0(x0+1)+y02
y02=3(1- )
x02
4
(-2≤ x0 ≤2)
OP·FP= (x0+2)2+2
1
4
当x0=2时,OP·FP取得最大值为6
当P,Q分别在椭圆短轴端点时,四边形PF1QF2的面积最大.
O
x
y
F
B
M
N
设M(x1,y1),N(x2,y2),
a2
x12
y12
b2
+ =1,
y22
b2
x22
a2
+ =1
y1-y2
x1-x2
y1+y2
x1+x2
·
=-
a2
b2
x1+x2=4,y1+y2=-2,
a2=2bc=b2+c2
b=c,a+c=4+2
a=4
O
x
y
F
E
N
M
E点为椭圆的右焦点,|MF|+|ME|=6,则
|MF|=6-|ME|,
|MF|+|MN|=6-(|ME|-|MN|)
当M,E,N三点共线时,|ME|-|MN|最大值为1,|MF|+|MN|最小值为5
例6. 点 M(x, y) 与定点 F(4, 0) 的距离和它到直线 l: 距离的比是常数 求点 M 的轨迹.
设 M 到 l 的距离为 d, 则
|MF|
d
=
4
5
(x-4)2+y2
| - x|
25
4
4
5
=
化简得 9x2+25y2=225,
x2
25
+ =1
y2
9
O
x
y
F
M
定点是右焦点,定直线叫右准线, 比值是离心率.
a2
c
x=
O
x
y
F
B
A
