2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.3.2抛物线的简单几何性质第二课时课件(14张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.3.2抛物线的简单几何性质第二课时课件(14张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 12:46:26 | ||
图片预览





文档简介
(共14张PPT)
3.3.2抛物线的简单几何性质
第二课时
新课程标准解读 核心素养
1.掌握直线与抛物线的位置关系的判断及相关问题.
2.能利用方程及数形结合思想解决焦点弦、弦中点等问题. 通过直线与抛物线的位置关系、焦点弦及中点弦、抛物线综合问题的学习,提升学生的逻辑推理、直观想象及数学运算的核心素养.
一、复习回顾:
y
x
o
y
x
o
y
x
o
二、 直线与抛物线的位置关系
1.直线与抛物线相离,无交点。
2.直线与抛物线相切,有一个交点。
3.直线与抛物线的对称轴平行,相交于一点。
4.直线与抛物线的对称轴不平行,相交与两点。
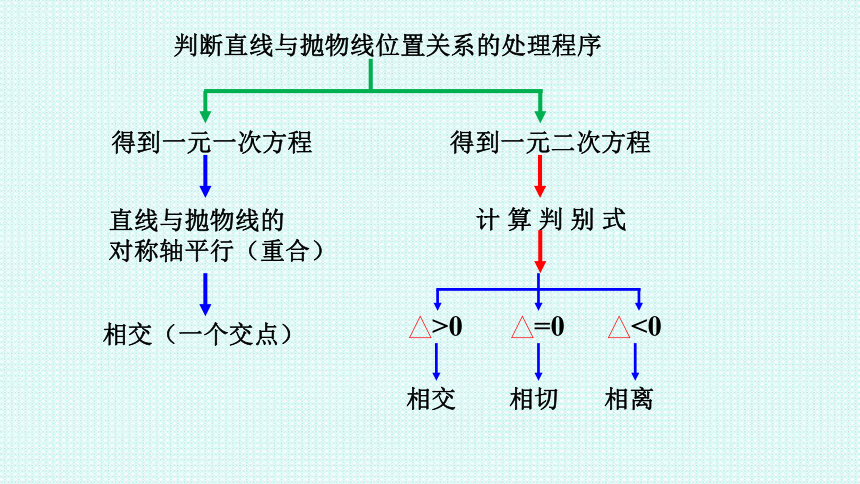
判断直线与抛物线位置关系的处理程序
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行(重合)
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
例1.(1)过定点P(0,1)作与抛物线y2=2x只有一个公共点的直线有几条?
(2)若直线l:y=(a+1)x-1与曲线C:y2=ax(a≠0)恰好有一个公共点,试求实数a的取值集合.
解:(1)当直线的斜率不存在时,直线x=0,符合题意.
P
当直线的斜率存在时,设过点P的直线方程为y=kx+1,当k=0时,直线l的方程为y=1,满足直线与抛物线y2=2x仅有一个公共点;
y=1
当k≠0时,将直线方程y=kx+1代入y2=2x,消去y得k2x2+2(k-1)x+1=0.由Δ=0,
(2)因为直线l与曲线C恰好有一个公共点,所以方程组
( )
消去y,得[(a+1)x-1]2=ax,
只有一组实数解,
即(a+1)2x2-(3a+2)x+1=0 ①.
当a=-1时,
满足
当a≠-1时,方程①是关于x的一元二次方程.
令Δ=(3a+2)2-4(a+1)2=a(5a+4)=0,
综上,实数a的取值集合是
若抛物线y2=4x与直线y=x-4相交于不同的两点A,B,求证OA⊥OB.
消去y,得x2-12x+16=0.
∵直线y=x-4与抛物线相交于不同两点A,B,
∴可设A(x1,y1),B(x2,y2),则有x1+x2=12,x1x2=16.
x1x2+y1y2=x1x2+(x1-4)(x2-4)
=x1x2+x1x2-4(x1+x2)+16
=16+16-4×12+16=0,
即OA⊥OB.
三、中点弦及弦长公式
例2:过点Q(4,1)作抛物线y2=8x的弦AB,恰被点Q所平分,求AB所在直线的方程.
Q
A
B
(点差法)设以Q为中点的弦AB的端点坐标为A(x1,y1),B(x2,y2),
∴(y1+y2)(y1-y2)=8(x1-x2).
又y1+y2=2,∴y1-y2=4(x1-x2),
∴kAB=4.
∴AB所在直线的方程为y-1=4(x-4),即4x-y-15=0.
法二:由题意知AB所在直线斜率存在,设A(x1,y1),B(x2,y2),弦AB所在直线的方程为y=k(x-4)+1.
( )
消去x,得ky2-8y-32k+8=0,
此方程的两根就是线段端点A,B两点的纵坐标.
又y1+y2=2,∴k=4.
∴AB所在直线的方程为4x-y-15=0.
例3:斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
法二: |AB |= |AF|+ |BF | = |AA1 |+ |BB1 |
=(x1+1)+(x2+1) =x1+x2+2=8
A
B
A1
B1
法一:F(1,0), AB的直线方程为 y=x-1,
y=x-1
y2=4x
x2-6x+1=0, x1+x2=6, x1x2=1,
|AB |=
(x1+x2)2-4x1x2
=8
还有其他的方法吗?
焦点弦长公式
经过抛物线焦点的直线与抛物线交于A, B两点,则称弦AB为抛物线的焦点弦.
设过抛物线 y2 = 2px (p>0) 焦点的直线交抛物线于A,B两点,设 A (x1, y1) ,B (x2, y2) ,则
焦点弦|AB|= (x1+x2) + p
A
B
|AB |= |AF|+ |BF | == x1+ +x2+ =x1+x2+p
p
2
p
2
1.已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.若直线l的倾斜角为60°,求|AB|的值.
2p=6,p=3,
F( ,0),
3
2
AB的直线方程为 y= (x- )
3
2
4x2-20x+9=0, x1+x2=5,
|AB|=8
2.设抛物线C:x2=4y焦点为F,直线y=kx+2与C交于A,B两点,且|AF|·|BF|=25,则k的值为 ( )
A.±2 B.-1 C.±1 D.-2
设A(x1,y1),B(x2,y2),将直线y=kx+2代入x2=4y,y2-(4+4k2)y+4=0,
所以y1·y2=4,y1+y2=4+4k2,
|AF|=y1+1,|BF|=y2+1,
|AF|·|BF|=y1·y2+(y1+y2)+1=4+4+4k2+1=25 k=±2.
p=4,所以y2=8x,
焦点F的坐标为(2,0),
2.直线y=kx+2与抛物线y2=8x有且只有一个公共点,则k=________.
当k=0时,直线与抛物线有唯一交点.
当k≠0时,联立方程消去y,得k2x2+4(k-2)x+4=0,
由题意Δ=16(k-2)2-16k2=0,解得k=1.
3.3.2抛物线的简单几何性质
第二课时
新课程标准解读 核心素养
1.掌握直线与抛物线的位置关系的判断及相关问题.
2.能利用方程及数形结合思想解决焦点弦、弦中点等问题. 通过直线与抛物线的位置关系、焦点弦及中点弦、抛物线综合问题的学习,提升学生的逻辑推理、直观想象及数学运算的核心素养.
一、复习回顾:
y
x
o
y
x
o
y
x
o
二、 直线与抛物线的位置关系
1.直线与抛物线相离,无交点。
2.直线与抛物线相切,有一个交点。
3.直线与抛物线的对称轴平行,相交于一点。
4.直线与抛物线的对称轴不平行,相交与两点。
判断直线与抛物线位置关系的处理程序
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行(重合)
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
例1.(1)过定点P(0,1)作与抛物线y2=2x只有一个公共点的直线有几条?
(2)若直线l:y=(a+1)x-1与曲线C:y2=ax(a≠0)恰好有一个公共点,试求实数a的取值集合.
解:(1)当直线的斜率不存在时,直线x=0,符合题意.
P
当直线的斜率存在时,设过点P的直线方程为y=kx+1,当k=0时,直线l的方程为y=1,满足直线与抛物线y2=2x仅有一个公共点;
y=1
当k≠0时,将直线方程y=kx+1代入y2=2x,消去y得k2x2+2(k-1)x+1=0.由Δ=0,
(2)因为直线l与曲线C恰好有一个公共点,所以方程组
( )
消去y,得[(a+1)x-1]2=ax,
只有一组实数解,
即(a+1)2x2-(3a+2)x+1=0 ①.
当a=-1时,
满足
当a≠-1时,方程①是关于x的一元二次方程.
令Δ=(3a+2)2-4(a+1)2=a(5a+4)=0,
综上,实数a的取值集合是
若抛物线y2=4x与直线y=x-4相交于不同的两点A,B,求证OA⊥OB.
消去y,得x2-12x+16=0.
∵直线y=x-4与抛物线相交于不同两点A,B,
∴可设A(x1,y1),B(x2,y2),则有x1+x2=12,x1x2=16.
x1x2+y1y2=x1x2+(x1-4)(x2-4)
=x1x2+x1x2-4(x1+x2)+16
=16+16-4×12+16=0,
即OA⊥OB.
三、中点弦及弦长公式
例2:过点Q(4,1)作抛物线y2=8x的弦AB,恰被点Q所平分,求AB所在直线的方程.
Q
A
B
(点差法)设以Q为中点的弦AB的端点坐标为A(x1,y1),B(x2,y2),
∴(y1+y2)(y1-y2)=8(x1-x2).
又y1+y2=2,∴y1-y2=4(x1-x2),
∴kAB=4.
∴AB所在直线的方程为y-1=4(x-4),即4x-y-15=0.
法二:由题意知AB所在直线斜率存在,设A(x1,y1),B(x2,y2),弦AB所在直线的方程为y=k(x-4)+1.
( )
消去x,得ky2-8y-32k+8=0,
此方程的两根就是线段端点A,B两点的纵坐标.
又y1+y2=2,∴k=4.
∴AB所在直线的方程为4x-y-15=0.
例3:斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
法二: |AB |= |AF|+ |BF | = |AA1 |+ |BB1 |
=(x1+1)+(x2+1) =x1+x2+2=8
A
B
A1
B1
法一:F(1,0), AB的直线方程为 y=x-1,
y=x-1
y2=4x
x2-6x+1=0, x1+x2=6, x1x2=1,
|AB |=
(x1+x2)2-4x1x2
=8
还有其他的方法吗?
焦点弦长公式
经过抛物线焦点的直线与抛物线交于A, B两点,则称弦AB为抛物线的焦点弦.
设过抛物线 y2 = 2px (p>0) 焦点的直线交抛物线于A,B两点,设 A (x1, y1) ,B (x2, y2) ,则
焦点弦|AB|= (x1+x2) + p
A
B
|AB |= |AF|+ |BF | == x1+ +x2+ =x1+x2+p
p
2
p
2
1.已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.若直线l的倾斜角为60°,求|AB|的值.
2p=6,p=3,
F( ,0),
3
2
AB的直线方程为 y= (x- )
3
2
4x2-20x+9=0, x1+x2=5,
|AB|=8
2.设抛物线C:x2=4y焦点为F,直线y=kx+2与C交于A,B两点,且|AF|·|BF|=25,则k的值为 ( )
A.±2 B.-1 C.±1 D.-2
设A(x1,y1),B(x2,y2),将直线y=kx+2代入x2=4y,y2-(4+4k2)y+4=0,
所以y1·y2=4,y1+y2=4+4k2,
|AF|=y1+1,|BF|=y2+1,
|AF|·|BF|=y1·y2+(y1+y2)+1=4+4+4k2+1=25 k=±2.
p=4,所以y2=8x,
焦点F的坐标为(2,0),
2.直线y=kx+2与抛物线y2=8x有且只有一个公共点,则k=________.
当k=0时,直线与抛物线有唯一交点.
当k≠0时,联立方程消去y,得k2x2+4(k-2)x+4=0,
由题意Δ=16(k-2)2-16k2=0,解得k=1.
