2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册第三章圆锥曲线习题课课件(32张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册第三章圆锥曲线习题课课件(32张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
圆锥曲线习题课
当m=3时,此时椭圆为
y2
9
x2
25
+ =1
c2=a2-b2=16,c=4,
F1(-4,0)
反之m2=25-16=9, m=±3,不满足,
x
y
o
x
y
o
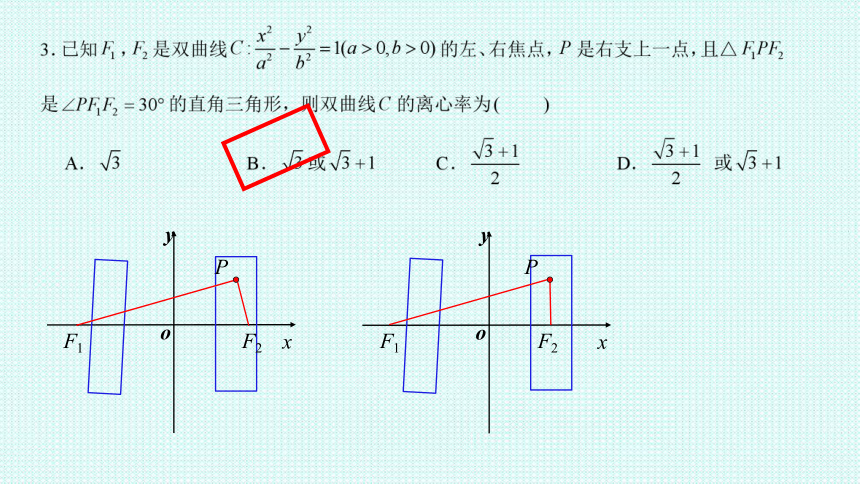
F1
F2
F1
F2
P
P
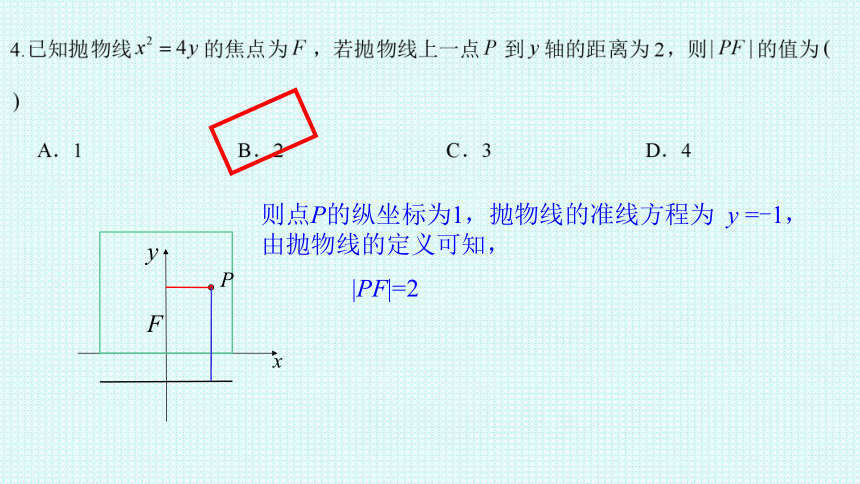
F
P
则点P的纵坐标为1,抛物线的准线方程为 y =-1,
由抛物线的定义可知,
|PF|=2
F
P
Q
M
N
E
如图:作QM垂直准线于M,PN垂直准线于N,
作PE⊥QM于E,
θ
|PE|=
x
y
O
F1
F2
M
P
Q
设P(x1,y1), Q(x2,y2),
M( a, b)
由原点O是PQM的重心,
x1+x2
=- a,
y1+y2
=- b,
a2
x12
y12
b2
+ =1,
y22
b2
x22
a2
+ =1
y1-y2
x1-x2
y1+y2
x1+x2
·
=-
a2
b2
a
b
=
1
2
x
y
o
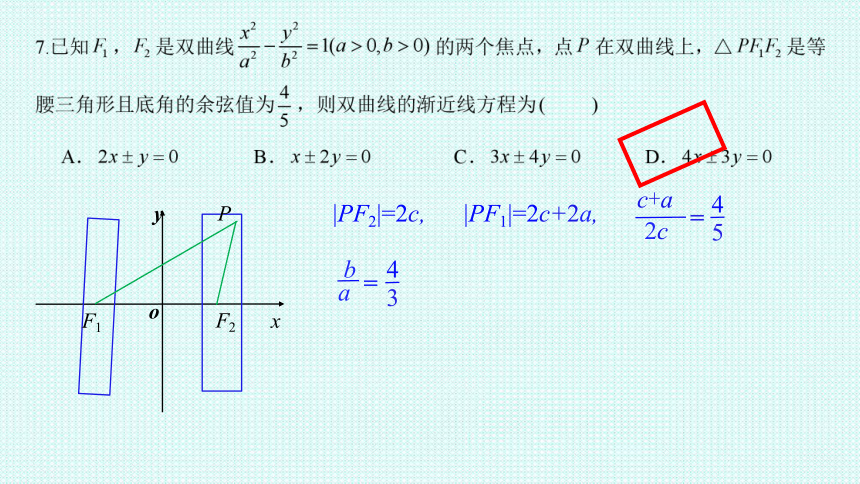
F1
F2
P
|PF2|=2c,
|PF1|=2c+2a,
c+a
2c
4
5
=
a
b
=
4
3
设双曲线的方程为
右焦点F到渐近线的距离为2,即b=2,
双曲线过点M( ,0)
所以双曲线的方程为
x2
3
- =1
y2
4
|AC|-|BC|=2 ,
sin∠BAC-sin∠ABC
sin∠ACB
=
|BC|-|AC|
|AB|
=-
7
x
y
o
F1
F2
A
B
M
双曲线的离心率为2,令a=m,c=2m,则b2=3m2,
所以双曲线的方程为
x2
m2
- =1
y2
3m2
设A(x1,y1), B(x2,y2),
y1-y2
x1-x2
=-6
x
y
o
F
P
Q
R
E
设双曲线左焦点为E,由对称性知四边形PEQF是平行四边形,|PE|=|QF|=2|FR|=2m,
|PF|=2m-2a,|RE|=m+2a,|PR|=3m-2a,
在Rt△PRE中,
(3m-2a)2+(2m)2=(m+2a)2
m= a
4
3
在Rt△PEF中,
|PE|2+|PF|2=4c2
a2=4c2
68
9
共轭双曲线是
y=± x
b
a
1
e12
1
e22
+ =1
e12e22=e12+e22
θ
A
B
x=my+
1
2
y2=2x
消去x得:y2-2my-1=0,
π
4
θ=
此时直线方程为
y=x-
1
2
|AB|=x1+x2+P=4
y1+y2=2m,x1+x2=m(y1+y2)+1=2m2+1
|AB|=2m2+2
圆心(m2+ , m)
1
2
圆心到准线的距离为 |AB|
1
2
A
B
θ
|AB|=x1+x2+P
当θ为锐角时,
|AF|=|AA1|=|MN|=P+|AF|cosθ,
A1
M
N
|AF|=
1-cosθ
P
当θ为钝角时,
依然成立
那么|BF|呢?
|BF|=
1+cosθ
P
|AB|= + =
1-cosθ
P
1+cosθ
P
sin2θ
2P
△OAB的面积可以分割为△OAF的面积加上△OBF的面积,
=
S△OAB= OF·AF + OF·BF
1
2
sin(π-θ)
1
2
sinθ
P
4
ABsinθ
=
2sinθ
P2
x
y
O
F1
F2
A
P
Q
M
设△AF1P内切圆圆心为M,另外切点为E,F,
E
F
|EF1|=|F1Q|=|FF2|=
2
|PF1|+|PF2|=|F1Q|+|QP|+|PF2|=|F1Q|+|FF2|=
4
F
P
Q
R
S
|QF|=|RF|=
p
4
|PF|=yP+
p
2
|SF|=yS+
p
2
|SR|=yS+
p
2
p
4
-
=yS+
p
4
|PQ|=yP+
p
2
p
4
-
=yP+
p
4
x2=2Py
x-6y+3P=0
2
yP=
p
6
yS=
3p
2
x
y
o
A
B
M
如图:作BD垂直于x轴,垂足为D,
D
A(a,0)
∠BAD=
π
3
∠MAO=
|OM|= a ,|AM|=2a,
|AD|=2a ,|BD|=2 a
B(3a,- 2 a)
9a2
a2
- =1
12a2
b2
a
b
=
2
y=± x
2
x
y
O
F1
F2
P
Q
|PF1|=|PQ|=|PF2|+|F2Q|
|PF1|-|PF2|=|F2Q|
2a=2,a=1,
由题意可得4-2m 0,即m 2,
c2=m2+1+4-2m=(m-1)2+4
所以当m=1时,焦距2c取得最小值,
所以双曲线的方程为
x2
2
- =1
y2
2
所以双曲线的右焦点为(2,0),
则抛物线y2=8x
x1+x2+P=8,
x1+x2=2,
∴线段AB中点的横坐标为2.
)
M
H
B
p
2
x0+ =
x02+8
又2Px0=8
y2=8x
M(1,2 )
H(-2,2 )
F(2,0)
过点B向抛物线的准线作垂线,垂足为G,
G
=
|HB|
|BF|
|HB|
|BG|
=
2
x
y
O
F
B
A
B(c, )
b2
a
a+c
2b2
a
a2+ac 2(c2-a2)
2e2-e-3 0
A
B
C
D
M
N
设CD中点为N,则
|MN|= ( |AC|+|BD|)
1
2
|MN|= ( |AF|+|BF|)= |AB|
1
2
1
2
因为直线l的斜率为 ,
所以|CD|=|AB|sin = |AB|
π
3
2
S△CMD=
2
|AB|=4,
设直线AB的方程为
y= ( )
x-
p
2
x1+x2= ,
5p
3
曲线C上任意一点(x,y)到原点的距离为
x2+y2
当x 0时,x2+y2-1=xy≤ ,当x=y时取等号
2
x2+y2
x
y
O
F1
F2
P
Q
( |F1P|+|F1F2|)·|F2P|=0
|F1P|=|F1F2|=2c
|F2P|=a, |F2P|=4|F2Q|
|F2Q|= a
1
4
|F2Q|= a
9
4
cos∠F1F2P= =
1
2
a
2c
a
4c
=
4c2+ a2- a2
1
16
81
16
2×2c× a
1
4
16c2=21a2
e=
4
x
y
O
F
P
A
B
H
E
如图,取AB中点H,椭圆另一个焦点为E,连结PE.
设OH=d,则PE=2d,PF=2a-2d
AH=
3
a-d
在Rt△OHA中,
OA2=OH2+AH2
a=5d
在Rt△OHF中,FH= a, OH= a,OF=c,
4
5
1
5
OF2=OH2+FH2
17a2=25c2
A
B
P
Q
(1)连接AQ,由线段AP的垂直平分线交直线BP于点Q.
|AQ|=|PQ|,
|QB|+|QA|=|QB|+|QP|=4 |AB|=2,
即Q是以A(1,0)、B(-1,0)为焦点的椭圆,…(3分),
2c=|AB|=2, c=1, |QB|+|QA|=2a=4, a=2,
点Q的轨迹方程:
x2
4
+ =1
y2
3
…(6分)
(2)设M(x,y),∵F(-1,0), OM=(x,y), FM=(x+1, y),
OM ·FM=x2+x+y2……(8分)
∵M是椭圆上任意一点,∴
y2=3(1- )
x2
4
OM ·FM=x2+x+y2= x2+x+3= (x+2)2+2
1
4
1
4
……(10分)
∵-2≤x≤2, ∴当x=2时,OM ·FM取最大值6.……(12分)
x
y
O
A
B
M
a=2b,
故可设椭圆E的方程为x2+4y2=4b2,①
由题意可得圆心M(﹣2,1)是线段AB的中点,
易知AB与x轴不垂直,记其方程为y=k(x+2)+1,代入①可得
(1+4k2)x2+8k(1+2k)x+4(1+2k)2﹣4b2=0,
且|AB|=
则x1+x2=
1+4k2
-8k(1+2k)
x1x2=
1+4k2
4(1+2k)2-4b2
x1+x2=﹣4,
=﹣4
1+4k2
-8k(1+2k)
k=
1
2
从而x1x2=8﹣2b2,
由|AB|=
解得b2=3,
则椭圆E的方程为
x2
12
+ =1
y2
3
由(1)可得AB的方程为:x﹣2y+4=0,
设平行AB且与椭圆相切的直线x﹣2y+m=0
m=±2
则dmax=
|2 +4|
故△PAB面积的最大值为S= × ×
1
2
|2 +4|
=
2 +2
y=± x
(1)抛物线的焦点F为(, 0),双曲线的渐近线方程为
p
2
3
x± y=0
2
| |
p
2
=1
解得P=4,故抛物线的方程为y2=8x,
(2)设P(x0,y0),由抛物线的定义可知
x0+ = 4,
p
2
x0= 2,
y0=± 4,
(2,± 4)
证明:(3)由题意知直线l不能与x轴平行,
故方程可设为x=my+n(n≠0),
x=my+n
y2=8x
消去x得y2-8my-8n=0
设A(x1,y1), B(x2,y2),
y1+y2=8m,
y1y2=-8n,
∵OA⊥OB,
∴x1x2+y1y2=0,
y1y2+ =0,
(y1y2)2
64
∵n≠0, ∴n=8
x=my+8,直线l恒过定点(8,0)
设双曲线的方程为
x2
9
- =1
y2
6
a2+b2=6,
双曲线C的方程为
x2
3
- =1
y2
3
(2)设直线l的方程为:y=m(m≠0)
y=m
x2-y2=3,
x=
m2+3
m2+3
或x=-
AM,BM的斜率分别为
kAM=-
m2+3
+
m
kAM=
m2+3
-
m
kAM·kAM=-1
故以AB为直径的圆过点M.
圆锥曲线习题课
当m=3时,此时椭圆为
y2
9
x2
25
+ =1
c2=a2-b2=16,c=4,
F1(-4,0)
反之m2=25-16=9, m=±3,不满足,
x
y
o
x
y
o
F1
F2
F1
F2
P
P
F
P
则点P的纵坐标为1,抛物线的准线方程为 y =-1,
由抛物线的定义可知,
|PF|=2
F
P
Q
M
N
E
如图:作QM垂直准线于M,PN垂直准线于N,
作PE⊥QM于E,
θ
|PE|=
x
y
O
F1
F2
M
P
Q
设P(x1,y1), Q(x2,y2),
M( a, b)
由原点O是PQM的重心,
x1+x2
=- a,
y1+y2
=- b,
a2
x12
y12
b2
+ =1,
y22
b2
x22
a2
+ =1
y1-y2
x1-x2
y1+y2
x1+x2
·
=-
a2
b2
a
b
=
1
2
x
y
o
F1
F2
P
|PF2|=2c,
|PF1|=2c+2a,
c+a
2c
4
5
=
a
b
=
4
3
设双曲线的方程为
右焦点F到渐近线的距离为2,即b=2,
双曲线过点M( ,0)
所以双曲线的方程为
x2
3
- =1
y2
4
|AC|-|BC|=2 ,
sin∠BAC-sin∠ABC
sin∠ACB
=
|BC|-|AC|
|AB|
=-
7
x
y
o
F1
F2
A
B
M
双曲线的离心率为2,令a=m,c=2m,则b2=3m2,
所以双曲线的方程为
x2
m2
- =1
y2
3m2
设A(x1,y1), B(x2,y2),
y1-y2
x1-x2
=-6
x
y
o
F
P
Q
R
E
设双曲线左焦点为E,由对称性知四边形PEQF是平行四边形,|PE|=|QF|=2|FR|=2m,
|PF|=2m-2a,|RE|=m+2a,|PR|=3m-2a,
在Rt△PRE中,
(3m-2a)2+(2m)2=(m+2a)2
m= a
4
3
在Rt△PEF中,
|PE|2+|PF|2=4c2
a2=4c2
68
9
共轭双曲线是
y=± x
b
a
1
e12
1
e22
+ =1
e12e22=e12+e22
θ
A
B
x=my+
1
2
y2=2x
消去x得:y2-2my-1=0,
π
4
θ=
此时直线方程为
y=x-
1
2
|AB|=x1+x2+P=4
y1+y2=2m,x1+x2=m(y1+y2)+1=2m2+1
|AB|=2m2+2
圆心(m2+ , m)
1
2
圆心到准线的距离为 |AB|
1
2
A
B
θ
|AB|=x1+x2+P
当θ为锐角时,
|AF|=|AA1|=|MN|=P+|AF|cosθ,
A1
M
N
|AF|=
1-cosθ
P
当θ为钝角时,
依然成立
那么|BF|呢?
|BF|=
1+cosθ
P
|AB|= + =
1-cosθ
P
1+cosθ
P
sin2θ
2P
△OAB的面积可以分割为△OAF的面积加上△OBF的面积,
=
S△OAB= OF·AF + OF·BF
1
2
sin(π-θ)
1
2
sinθ
P
4
ABsinθ
=
2sinθ
P2
x
y
O
F1
F2
A
P
Q
M
设△AF1P内切圆圆心为M,另外切点为E,F,
E
F
|EF1|=|F1Q|=|FF2|=
2
|PF1|+|PF2|=|F1Q|+|QP|+|PF2|=|F1Q|+|FF2|=
4
F
P
Q
R
S
|QF|=|RF|=
p
4
|PF|=yP+
p
2
|SF|=yS+
p
2
|SR|=yS+
p
2
p
4
-
=yS+
p
4
|PQ|=yP+
p
2
p
4
-
=yP+
p
4
x2=2Py
x-6y+3P=0
2
yP=
p
6
yS=
3p
2
x
y
o
A
B
M
如图:作BD垂直于x轴,垂足为D,
D
A(a,0)
∠BAD=
π
3
∠MAO=
|OM|= a ,|AM|=2a,
|AD|=2a ,|BD|=2 a
B(3a,- 2 a)
9a2
a2
- =1
12a2
b2
a
b
=
2
y=± x
2
x
y
O
F1
F2
P
Q
|PF1|=|PQ|=|PF2|+|F2Q|
|PF1|-|PF2|=|F2Q|
2a=2,a=1,
由题意可得4-2m 0,即m 2,
c2=m2+1+4-2m=(m-1)2+4
所以当m=1时,焦距2c取得最小值,
所以双曲线的方程为
x2
2
- =1
y2
2
所以双曲线的右焦点为(2,0),
则抛物线y2=8x
x1+x2+P=8,
x1+x2=2,
∴线段AB中点的横坐标为2.
)
M
H
B
p
2
x0+ =
x02+8
又2Px0=8
y2=8x
M(1,2 )
H(-2,2 )
F(2,0)
过点B向抛物线的准线作垂线,垂足为G,
G
=
|HB|
|BF|
|HB|
|BG|
=
2
x
y
O
F
B
A
B(c, )
b2
a
a+c
2b2
a
a2+ac 2(c2-a2)
2e2-e-3 0
A
B
C
D
M
N
设CD中点为N,则
|MN|= ( |AC|+|BD|)
1
2
|MN|= ( |AF|+|BF|)= |AB|
1
2
1
2
因为直线l的斜率为 ,
所以|CD|=|AB|sin = |AB|
π
3
2
S△CMD=
2
|AB|=4,
设直线AB的方程为
y= ( )
x-
p
2
x1+x2= ,
5p
3
曲线C上任意一点(x,y)到原点的距离为
x2+y2
当x 0时,x2+y2-1=xy≤ ,当x=y时取等号
2
x2+y2
x
y
O
F1
F2
P
Q
( |F1P|+|F1F2|)·|F2P|=0
|F1P|=|F1F2|=2c
|F2P|=a, |F2P|=4|F2Q|
|F2Q|= a
1
4
|F2Q|= a
9
4
cos∠F1F2P= =
1
2
a
2c
a
4c
=
4c2+ a2- a2
1
16
81
16
2×2c× a
1
4
16c2=21a2
e=
4
x
y
O
F
P
A
B
H
E
如图,取AB中点H,椭圆另一个焦点为E,连结PE.
设OH=d,则PE=2d,PF=2a-2d
AH=
3
a-d
在Rt△OHA中,
OA2=OH2+AH2
a=5d
在Rt△OHF中,FH= a, OH= a,OF=c,
4
5
1
5
OF2=OH2+FH2
17a2=25c2
A
B
P
Q
(1)连接AQ,由线段AP的垂直平分线交直线BP于点Q.
|AQ|=|PQ|,
|QB|+|QA|=|QB|+|QP|=4 |AB|=2,
即Q是以A(1,0)、B(-1,0)为焦点的椭圆,…(3分),
2c=|AB|=2, c=1, |QB|+|QA|=2a=4, a=2,
点Q的轨迹方程:
x2
4
+ =1
y2
3
…(6分)
(2)设M(x,y),∵F(-1,0), OM=(x,y), FM=(x+1, y),
OM ·FM=x2+x+y2……(8分)
∵M是椭圆上任意一点,∴
y2=3(1- )
x2
4
OM ·FM=x2+x+y2= x2+x+3= (x+2)2+2
1
4
1
4
……(10分)
∵-2≤x≤2, ∴当x=2时,OM ·FM取最大值6.……(12分)
x
y
O
A
B
M
a=2b,
故可设椭圆E的方程为x2+4y2=4b2,①
由题意可得圆心M(﹣2,1)是线段AB的中点,
易知AB与x轴不垂直,记其方程为y=k(x+2)+1,代入①可得
(1+4k2)x2+8k(1+2k)x+4(1+2k)2﹣4b2=0,
且|AB|=
则x1+x2=
1+4k2
-8k(1+2k)
x1x2=
1+4k2
4(1+2k)2-4b2
x1+x2=﹣4,
=﹣4
1+4k2
-8k(1+2k)
k=
1
2
从而x1x2=8﹣2b2,
由|AB|=
解得b2=3,
则椭圆E的方程为
x2
12
+ =1
y2
3
由(1)可得AB的方程为:x﹣2y+4=0,
设平行AB且与椭圆相切的直线x﹣2y+m=0
m=±2
则dmax=
|2 +4|
故△PAB面积的最大值为S= × ×
1
2
|2 +4|
=
2 +2
y=± x
(1)抛物线的焦点F为(, 0),双曲线的渐近线方程为
p
2
3
x± y=0
2
| |
p
2
=1
解得P=4,故抛物线的方程为y2=8x,
(2)设P(x0,y0),由抛物线的定义可知
x0+ = 4,
p
2
x0= 2,
y0=± 4,
(2,± 4)
证明:(3)由题意知直线l不能与x轴平行,
故方程可设为x=my+n(n≠0),
x=my+n
y2=8x
消去x得y2-8my-8n=0
设A(x1,y1), B(x2,y2),
y1+y2=8m,
y1y2=-8n,
∵OA⊥OB,
∴x1x2+y1y2=0,
y1y2+ =0,
(y1y2)2
64
∵n≠0, ∴n=8
x=my+8,直线l恒过定点(8,0)
设双曲线的方程为
x2
9
- =1
y2
6
a2+b2=6,
双曲线C的方程为
x2
3
- =1
y2
3
(2)设直线l的方程为:y=m(m≠0)
y=m
x2-y2=3,
x=
m2+3
m2+3
或x=-
AM,BM的斜率分别为
kAM=-
m2+3
+
m
kAM=
m2+3
-
m
kAM·kAM=-1
故以AB为直径的圆过点M.
