2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.3.1抛物线及其标准方程课件(18张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.3.1抛物线及其标准方程课件(18张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 9.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 12:50:56 | ||
图片预览






文档简介
(共18张PPT)
3.3.1抛物线及其标准方程
生活中存在着各种形式的抛物线
新课程标准解读 核心素养
1.了解抛物线的实际背景,感受抛物线在刻画现实世界和解决实际问题中的作用.
2.了解抛物线的定义、几何图形和标准方程. 1.数学抽象:结合教材实例了解抛物线的义.
2.逻辑推理、数学运算:抛物线的标准方程的推导及求解.
抛物线及其标准方程(一)
球在空中运动的轨迹是抛物线规律,那么抛物线它有怎样的几何特征呢
二次函数y=ax2+bx+c=0(a≠0)又到底是一条怎样的抛物线
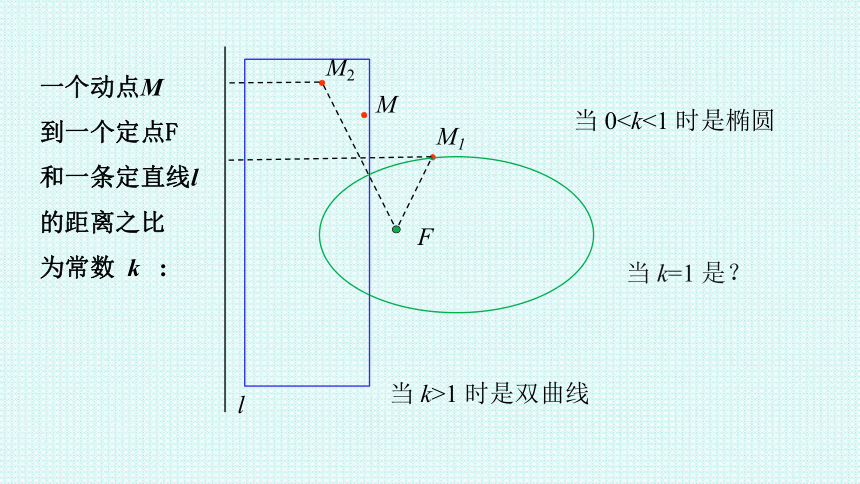
一个动点M
到一个定点F
和一条定直线l
的距离之比
为常数 k :
l
F
M1
当 0M2
当 k>1 时是双曲线
M
当 k=1 是?
如图,把一根直尺固定在画图板内直尺l的位置上,截取一根绳子的长度等于AC的长度,现将绳子的一端固定在三角板的顶点A处,另一端用图钉固定在F处;用一支粉笔扣着绳子,紧靠着三角板的这条直角边把绳子绷紧,然后使三角板紧靠着直尺上下滑动,这样粉笔就描出了一条曲线.
0
1
2
3
4
5
6
7
8
9
10
A
C
一、抛物线的定义:
平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线
F
M
l
H
其中 定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线
定直线l不经过定点F.
定义中包含三个定值,分别为一个定点,
一条定直线及一个确定的比值.
二、标准方程的推导
设焦点到准线的距离为常数P(P>0)如何建立坐标系,求出抛物线的标准方程呢?
x
y
o
F
M
l
H
●
(1)y2=2px
F
M
l
H
●
x
y
o
(2)y2=2px-p2
F
M
l
H
●
x
y
(3)y2=2px+p2
F
M
l
H
●
取过焦点F且垂直于准线 l 的直线为x轴,x轴与l 交于K,以线段KF的中点为原点, 建立直角坐标系
x
y
o
设︱KF︱= p
K
则F( ,0), l :x = -
p
2
p
2
设点M的坐标为(x,y),
化简得 y2 = 2px(p>0)
三、抛物线的标准方程
不同点:(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口方向坐标轴的正(负)方向.
相同点:(1)顶点为原点;(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶点到准线的距离为 .
p
2
p
2
把方程 y2 = 2px (p>0)叫做抛物线的标准方程.其中 p 为正常数,表示焦点在 x 轴正半轴上.p的几何意义是焦点到准线的距离,焦点坐标( ,0),准线方程是x=
p
2
因坐标系的建立
不同,故有四种
情况。
四种抛物线的对比
图 形
标准方程
焦点坐标
准线方程
y2=2px
(p>0)
p
2
( , 0)
p
2
x=-
y2=-2px
(p>0)
p
2
( - , 0)
p
2
x=
x2=2py
(p>0)
p
2
(0, )
p
2
y=-
x2=-2py
(p>0)
p
2
(0, - )
p
2
y=
P的意义:抛物线的焦点到准线的距离
方程的特点:
(1)左边是二次式,
(2)右边是一次式;
决定了焦点的位置.
探究点1 抛物线的标准方程
例1.试求满足下列条件的抛物线的标准方程.
(1)过点(-3,2);
(2)焦点在直线x-2y-4=0上.
解:(1)因为点(-3,2)在第二象限,
所以抛物线的标准方程可设为y2=-2px(p>0)或x2=2py(p>0),
把点(-3,2)分别代入
所以所求抛物线的标准方程为
(2)令x=0,得y=-2;令y=0,得x=4.
故抛物线的焦点为(4,0)或(0,-2).
由直线方程如何找焦点
当焦点为(4,0)时,
即2p=16,此时抛物线方程为y2=16x.
当焦点为(0,-2)时,
此时抛物线方程为x2=-8y.
故所求抛物线的标准方程为y2=16x或x2=-8y.
根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
(1)左顶点为(-3,0),
方程为y2=-12x.
又(-3)2=2pm,所以p=±1或p=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
A
抛物线标准方程的求法
(1)定义法:建立适当的坐标系,利用抛物线的定义列出动点满足的条件,列出方程,进行化简,根据定义求出p,最后写出标准方程.
(2)待定系数法:由于标准方程有四种形式,因而在求方程时应首先确定焦点在哪一个半轴上,进而确定方程的形式,然后再利用已知条件确定p的值.
探究点2 抛物线定义的应用
例2. (1)若动圆M与圆C:(x-2)2+y2=1外切,又与直线x+1=0相切,求动圆圆心的轨迹方程;
(2)已知点P是抛物线y2=2x上的一个动点,求点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值.
(1)设M(x,y),半径为R,由已知得定圆圆心为C(2,0),半径r=1.因为两圆外切,所以|MC|=R+1.又动圆M与已知直线x+1=0相切,所以圆心M到直线x+1=0的距离d=R.所以|MC|=d+1.
即动点M到定点C(2,0)的距离等于它到定直线x+2=0的距离.
故其方程为y2=8x.
P
(2)由抛物线的定义可知,抛物线上的点到准线的距离等于到焦点的距离.
由图可知,点P,点(0,2)和抛物线的
焦点
三点共线时距离之和最小,
(变条件)若将本例(2)中的点(0,2)改为点A(3,2),其他条件不变,求|PA|+|PF|的最小值.
A
P
由图可知,当PA⊥l时,|PA|+d最小,
在抛物线中求解与焦点有关的两点间距离和的最小值时,往往用抛物线的定义进行转化,即化折线为直线解决最值问题.
3.3.1抛物线及其标准方程
生活中存在着各种形式的抛物线
新课程标准解读 核心素养
1.了解抛物线的实际背景,感受抛物线在刻画现实世界和解决实际问题中的作用.
2.了解抛物线的定义、几何图形和标准方程. 1.数学抽象:结合教材实例了解抛物线的义.
2.逻辑推理、数学运算:抛物线的标准方程的推导及求解.
抛物线及其标准方程(一)
球在空中运动的轨迹是抛物线规律,那么抛物线它有怎样的几何特征呢
二次函数y=ax2+bx+c=0(a≠0)又到底是一条怎样的抛物线
一个动点M
到一个定点F
和一条定直线l
的距离之比
为常数 k :
l
F
M1
当 0
当 k>1 时是双曲线
M
当 k=1 是?
如图,把一根直尺固定在画图板内直尺l的位置上,截取一根绳子的长度等于AC的长度,现将绳子的一端固定在三角板的顶点A处,另一端用图钉固定在F处;用一支粉笔扣着绳子,紧靠着三角板的这条直角边把绳子绷紧,然后使三角板紧靠着直尺上下滑动,这样粉笔就描出了一条曲线.
0
1
2
3
4
5
6
7
8
9
10
A
C
一、抛物线的定义:
平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线
F
M
l
H
其中 定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线
定直线l不经过定点F.
定义中包含三个定值,分别为一个定点,
一条定直线及一个确定的比值.
二、标准方程的推导
设焦点到准线的距离为常数P(P>0)如何建立坐标系,求出抛物线的标准方程呢?
x
y
o
F
M
l
H
●
(1)y2=2px
F
M
l
H
●
x
y
o
(2)y2=2px-p2
F
M
l
H
●
x
y
(3)y2=2px+p2
F
M
l
H
●
取过焦点F且垂直于准线 l 的直线为x轴,x轴与l 交于K,以线段KF的中点为原点, 建立直角坐标系
x
y
o
设︱KF︱= p
K
则F( ,0), l :x = -
p
2
p
2
设点M的坐标为(x,y),
化简得 y2 = 2px(p>0)
三、抛物线的标准方程
不同点:(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口方向坐标轴的正(负)方向.
相同点:(1)顶点为原点;(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶点到准线的距离为 .
p
2
p
2
把方程 y2 = 2px (p>0)叫做抛物线的标准方程.其中 p 为正常数,表示焦点在 x 轴正半轴上.p的几何意义是焦点到准线的距离,焦点坐标( ,0),准线方程是x=
p
2
因坐标系的建立
不同,故有四种
情况。
四种抛物线的对比
图 形
标准方程
焦点坐标
准线方程
y2=2px
(p>0)
p
2
( , 0)
p
2
x=-
y2=-2px
(p>0)
p
2
( - , 0)
p
2
x=
x2=2py
(p>0)
p
2
(0, )
p
2
y=-
x2=-2py
(p>0)
p
2
(0, - )
p
2
y=
P的意义:抛物线的焦点到准线的距离
方程的特点:
(1)左边是二次式,
(2)右边是一次式;
决定了焦点的位置.
探究点1 抛物线的标准方程
例1.试求满足下列条件的抛物线的标准方程.
(1)过点(-3,2);
(2)焦点在直线x-2y-4=0上.
解:(1)因为点(-3,2)在第二象限,
所以抛物线的标准方程可设为y2=-2px(p>0)或x2=2py(p>0),
把点(-3,2)分别代入
所以所求抛物线的标准方程为
(2)令x=0,得y=-2;令y=0,得x=4.
故抛物线的焦点为(4,0)或(0,-2).
由直线方程如何找焦点
当焦点为(4,0)时,
即2p=16,此时抛物线方程为y2=16x.
当焦点为(0,-2)时,
此时抛物线方程为x2=-8y.
故所求抛物线的标准方程为y2=16x或x2=-8y.
根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
(1)左顶点为(-3,0),
方程为y2=-12x.
又(-3)2=2pm,所以p=±1或p=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
A
抛物线标准方程的求法
(1)定义法:建立适当的坐标系,利用抛物线的定义列出动点满足的条件,列出方程,进行化简,根据定义求出p,最后写出标准方程.
(2)待定系数法:由于标准方程有四种形式,因而在求方程时应首先确定焦点在哪一个半轴上,进而确定方程的形式,然后再利用已知条件确定p的值.
探究点2 抛物线定义的应用
例2. (1)若动圆M与圆C:(x-2)2+y2=1外切,又与直线x+1=0相切,求动圆圆心的轨迹方程;
(2)已知点P是抛物线y2=2x上的一个动点,求点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值.
(1)设M(x,y),半径为R,由已知得定圆圆心为C(2,0),半径r=1.因为两圆外切,所以|MC|=R+1.又动圆M与已知直线x+1=0相切,所以圆心M到直线x+1=0的距离d=R.所以|MC|=d+1.
即动点M到定点C(2,0)的距离等于它到定直线x+2=0的距离.
故其方程为y2=8x.
P
(2)由抛物线的定义可知,抛物线上的点到准线的距离等于到焦点的距离.
由图可知,点P,点(0,2)和抛物线的
焦点
三点共线时距离之和最小,
(变条件)若将本例(2)中的点(0,2)改为点A(3,2),其他条件不变,求|PA|+|PF|的最小值.
A
P
由图可知,当PA⊥l时,|PA|+d最小,
在抛物线中求解与焦点有关的两点间距离和的最小值时,往往用抛物线的定义进行转化,即化折线为直线解决最值问题.
