《倍长中线法》教学课件-人教版初中数学八年级上册第13章全等三角形(15张PPT)
文档属性
| 名称 | 《倍长中线法》教学课件-人教版初中数学八年级上册第13章全等三角形(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 16:42:46 | ||
图片预览



文档简介
(共15张PPT)
倍长中线法
*
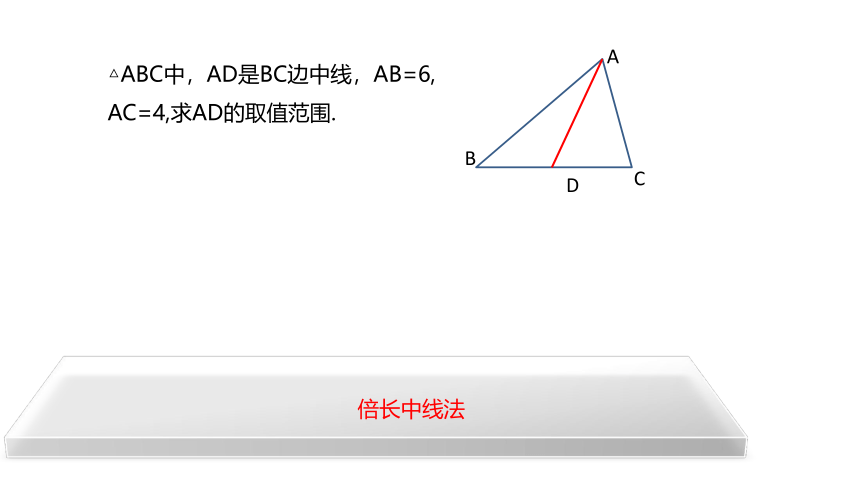
△ABC中,AD是BC边中线,AB=6,
AC=4,求AD的取值范围.
A
B
C
D
倍长中线法
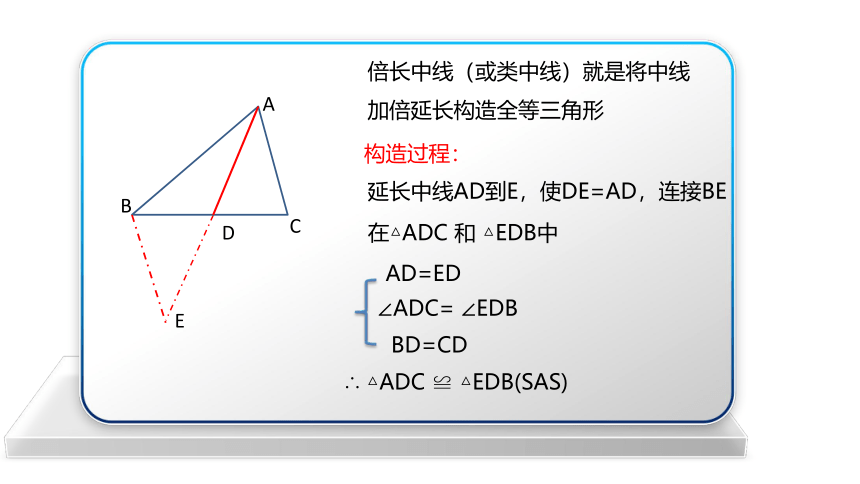
倍长中线(或类中线)就是将中线加倍延长构造全等三角形
A
B
C
D
E
BD=CD
构造过程:
延长中线AD到E,使DE=AD,连接BE
在△ADC 和 △EDB中
∴ △ADC ≌ △EDB(SAS)
AD=ED
∠ADC= ∠EDB
倍长中线可以直接倍长或间接倍长(或类倍长)
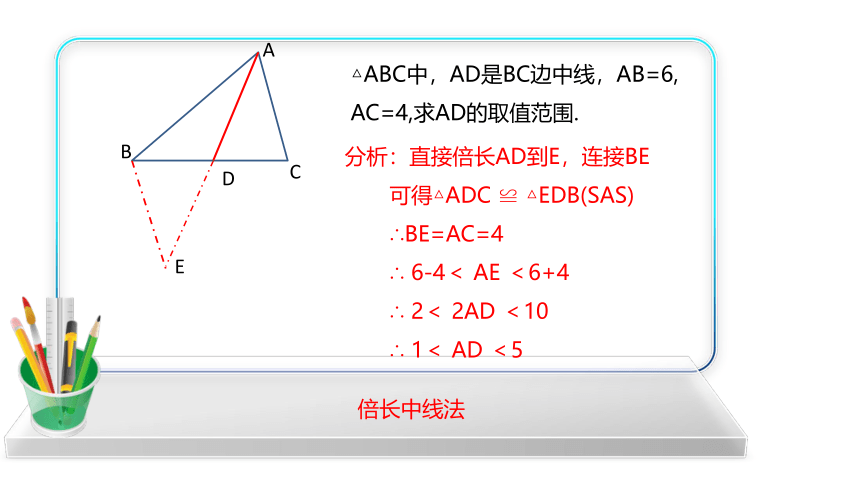
△ABC中,AD是BC边中线,AB=6,
AC=4,求AD的取值范围.
分析:直接倍长AD到E,连接BE
可得△ADC ≌ △EDB(SAS)
∴BE=AC=4
∴ 6-4< AE <6+4
∴ 2< 2AD <10
∴ 1< AD <5
A
B
C
D
E
倍长中线法
已知,如图,在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
D
A
B
F
C
E
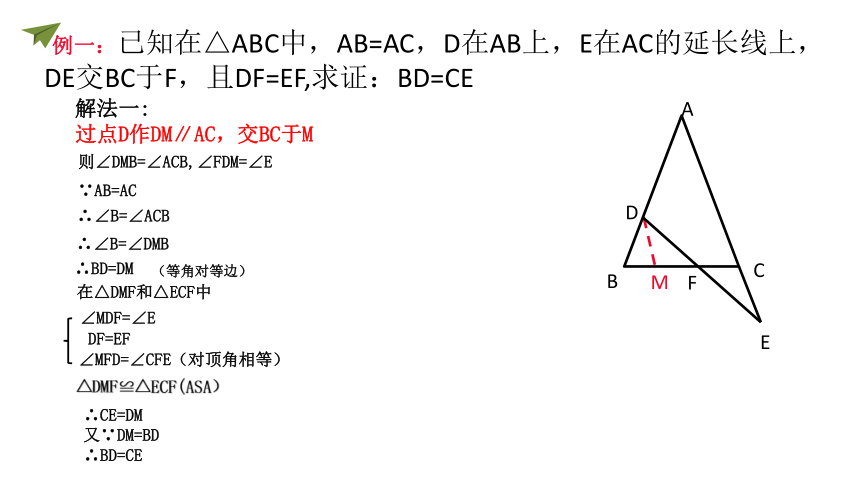
例一:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
△DMF≌△ECF(ASA)
M
D
A
B
F
C
E
解法一:
过点D作DM∥AC,交BC于M
∴BD=DM
∴CE=DM
又∵DM=BD
∴BD=CE
(等角对等边)
则∠DMB=∠ACB,∠FDM=∠E
∵AB=AC
∴∠B=∠ACB
∴∠B=∠DMB
在△DMF和△ECF中
∠MDF=∠E
DF=EF
∠MFD=∠CFE(对顶角相等)
例一:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
∵EG∥AB
∴∠B=∠G
∵AB=AC
∴∠B=∠ACB
又∵∠ACB=∠ECG
∴∠G=∠ECG,CE=GE
在△BDF和△GEF中
∠B=∠G
∠BFD=∠EFG
DF=EF
△BDF≌△GEF(AAS)
GE=BD
∵CE=GE ∴BD=CE
D
A
B
F
C
E
G
解法二:
过点E作EG∥AB,交BC的延长线于点G
例一:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
∵AB=AC, ∠ECN=∠ACB
∴∠ABC=∠ACB=∠ECN
在△DMB和△ENC中
∠ECN=∠ABC
∠DMF=∠ENF=90°
DM=EN
∴ (AAS)
∴BD=CE
D
A
B
F
C
E
N
M
解法三:
过点D作DM⊥BC,交BC于M,过点E作EN⊥BC,交BC延长线于N
在△DMF和△ENF中
∠DMF= ∠ENF=90°
∠ MFC=∠ NFE
DF=EF
∴△DMF≌△ENF(AAS)
∴DM=EN
△DMB≌△ENC
例二:
如图,已知△ABC中,AD是中线,AE是△ABD的中线,BA=BD
求证:AC=2AE
A
B
E
D
C
F
解:延长AE到F,使EF=AE,连接DF,
∵AE是△ABD的中线,∴BE=ED
在△ABE与△FDE中,
BE=DE,∠AEB=∠DEF ,AE=EF
∴△ABE≌△FDE(SAS)
∴AB=DF,∠B=∠BDF,
∵∠ADC是△ADB的外角,
∴∠ADC=∠BAD+∠B
∵∠BAD=∠BDA ∠B=∠BDF
构造2AE,可证△ADF≌△ADC
解:
例二:
如图,已知△ABC中,AD是中线,AE是△ABD的中线,BA=BD,∠BAD=∠BDA求证:AC=2AE
A
B
E
D
C
F
∴∠ADC=∠BDA+∠BDF,
∴∠ADF=∠ADC,
在△ADF与△ADC中,
AD=AD,∠ADF=∠ADC ,FD=DC
∴△ADF≌△ADC(SAS)
∴AF=AC
∴AC=2AE
小结
实际上,由倍长中线时的操作便可知,我们总是能通过构造全等三角形,将一些看似“分散”的条件聚集起来,从而将问题明晰。
总结回顾
边上“中点”,联想倍长中线法作相关辅助线求解
倍长中线法只是解题的第一步,找准全等三角形、注重内错角、同旁内角、对顶角、等边等角的转化
掌握几种基本辅助线模型,根据实际已知条件灵活运用,作垂线、平行线是倍长中线法的补充
多观察
多练习
A
C
B
E
D
F
A
C
B
N
D
M
A
C
B
E
D
多尝试
专题讨论:
有人说直角三角形斜边中线等于斜
边一半,你认为对吗,为什么?
C
A
B
D
C
A
B
D
E
△ADC ≌ △EDB(SAS)
△ABC ≌ △ECB(SAS)
倍长中线法
*
△ABC中,AD是BC边中线,AB=6,
AC=4,求AD的取值范围.
A
B
C
D
倍长中线法
倍长中线(或类中线)就是将中线加倍延长构造全等三角形
A
B
C
D
E
BD=CD
构造过程:
延长中线AD到E,使DE=AD,连接BE
在△ADC 和 △EDB中
∴ △ADC ≌ △EDB(SAS)
AD=ED
∠ADC= ∠EDB
倍长中线可以直接倍长或间接倍长(或类倍长)
△ABC中,AD是BC边中线,AB=6,
AC=4,求AD的取值范围.
分析:直接倍长AD到E,连接BE
可得△ADC ≌ △EDB(SAS)
∴BE=AC=4
∴ 6-4< AE <6+4
∴ 2< 2AD <10
∴ 1< AD <5
A
B
C
D
E
倍长中线法
已知,如图,在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
D
A
B
F
C
E
例一:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
△DMF≌△ECF(ASA)
M
D
A
B
F
C
E
解法一:
过点D作DM∥AC,交BC于M
∴BD=DM
∴CE=DM
又∵DM=BD
∴BD=CE
(等角对等边)
则∠DMB=∠ACB,∠FDM=∠E
∵AB=AC
∴∠B=∠ACB
∴∠B=∠DMB
在△DMF和△ECF中
∠MDF=∠E
DF=EF
∠MFD=∠CFE(对顶角相等)
例一:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
∵EG∥AB
∴∠B=∠G
∵AB=AC
∴∠B=∠ACB
又∵∠ACB=∠ECG
∴∠G=∠ECG,CE=GE
在△BDF和△GEF中
∠B=∠G
∠BFD=∠EFG
DF=EF
△BDF≌△GEF(AAS)
GE=BD
∵CE=GE ∴BD=CE
D
A
B
F
C
E
G
解法二:
过点E作EG∥AB,交BC的延长线于点G
例一:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
∵AB=AC, ∠ECN=∠ACB
∴∠ABC=∠ACB=∠ECN
在△DMB和△ENC中
∠ECN=∠ABC
∠DMF=∠ENF=90°
DM=EN
∴ (AAS)
∴BD=CE
D
A
B
F
C
E
N
M
解法三:
过点D作DM⊥BC,交BC于M,过点E作EN⊥BC,交BC延长线于N
在△DMF和△ENF中
∠DMF= ∠ENF=90°
∠ MFC=∠ NFE
DF=EF
∴△DMF≌△ENF(AAS)
∴DM=EN
△DMB≌△ENC
例二:
如图,已知△ABC中,AD是中线,AE是△ABD的中线,BA=BD
求证:AC=2AE
A
B
E
D
C
F
解:延长AE到F,使EF=AE,连接DF,
∵AE是△ABD的中线,∴BE=ED
在△ABE与△FDE中,
BE=DE,∠AEB=∠DEF ,AE=EF
∴△ABE≌△FDE(SAS)
∴AB=DF,∠B=∠BDF,
∵∠ADC是△ADB的外角,
∴∠ADC=∠BAD+∠B
∵∠BAD=∠BDA ∠B=∠BDF
构造2AE,可证△ADF≌△ADC
解:
例二:
如图,已知△ABC中,AD是中线,AE是△ABD的中线,BA=BD,∠BAD=∠BDA求证:AC=2AE
A
B
E
D
C
F
∴∠ADC=∠BDA+∠BDF,
∴∠ADF=∠ADC,
在△ADF与△ADC中,
AD=AD,∠ADF=∠ADC ,FD=DC
∴△ADF≌△ADC(SAS)
∴AF=AC
∴AC=2AE
小结
实际上,由倍长中线时的操作便可知,我们总是能通过构造全等三角形,将一些看似“分散”的条件聚集起来,从而将问题明晰。
总结回顾
边上“中点”,联想倍长中线法作相关辅助线求解
倍长中线法只是解题的第一步,找准全等三角形、注重内错角、同旁内角、对顶角、等边等角的转化
掌握几种基本辅助线模型,根据实际已知条件灵活运用,作垂线、平行线是倍长中线法的补充
多观察
多练习
A
C
B
E
D
F
A
C
B
N
D
M
A
C
B
E
D
多尝试
专题讨论:
有人说直角三角形斜边中线等于斜
边一半,你认为对吗,为什么?
C
A
B
D
C
A
B
D
E
△ADC ≌ △EDB(SAS)
△ABC ≌ △ECB(SAS)
