人教版八年级数学下册17.2 勾股定理的逆定理-第2课时 勾股定理及其逆定理的综合应用(word版含答案)
文档属性
| 名称 | 人教版八年级数学下册17.2 勾股定理的逆定理-第2课时 勾股定理及其逆定理的综合应用(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 280.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 00:00:00 | ||
图片预览

文档简介
八下-第十七章 勾股定理-17.2 勾股定理的逆定理-第2课时 勾股定理及其逆定理的综合应用
一、选择题(共3小题;共15分)
1. 下列几组数中,为勾股数的是
A. ,, B. ,, C. ,, D. ,,
2. 一辆汽车从点 出发沿正东方向行驶 到达点 ,然后转向行驶 到达点 ,最后从点 沿 方向直接回到出发点 .如果汽车从出发到返回共行驶了 ,那么 的方向是
A. 正东或正西 B. 正南 C. 正北 D. 正南或正北
3. 有五根小木棒,其长度分别为 ,,,,,现将他们摆成两个直角三角形,其中正确的是
A. B.
C. D.
二、填空题(共6小题;共30分)
4. 下列 组数:① ,,;② ,,;③ ,,;④ ,,.其中是勾股数的为 (填序号).
5. 观察以下几组勾股数,并寻找规律:
① ,,;② ,,;③ ,,;④ ,,; 请你写出有以上规律的第⑤组勾股数: .
6. 一根电线杆高 ,为了安全起见,在电线杆顶部到与电线杆底部水平距离 处加一拉线.拉线工人发现所用线长为 米(不计捆缚部分),则电线杆与地面 (填“垂直”或“不垂直”).
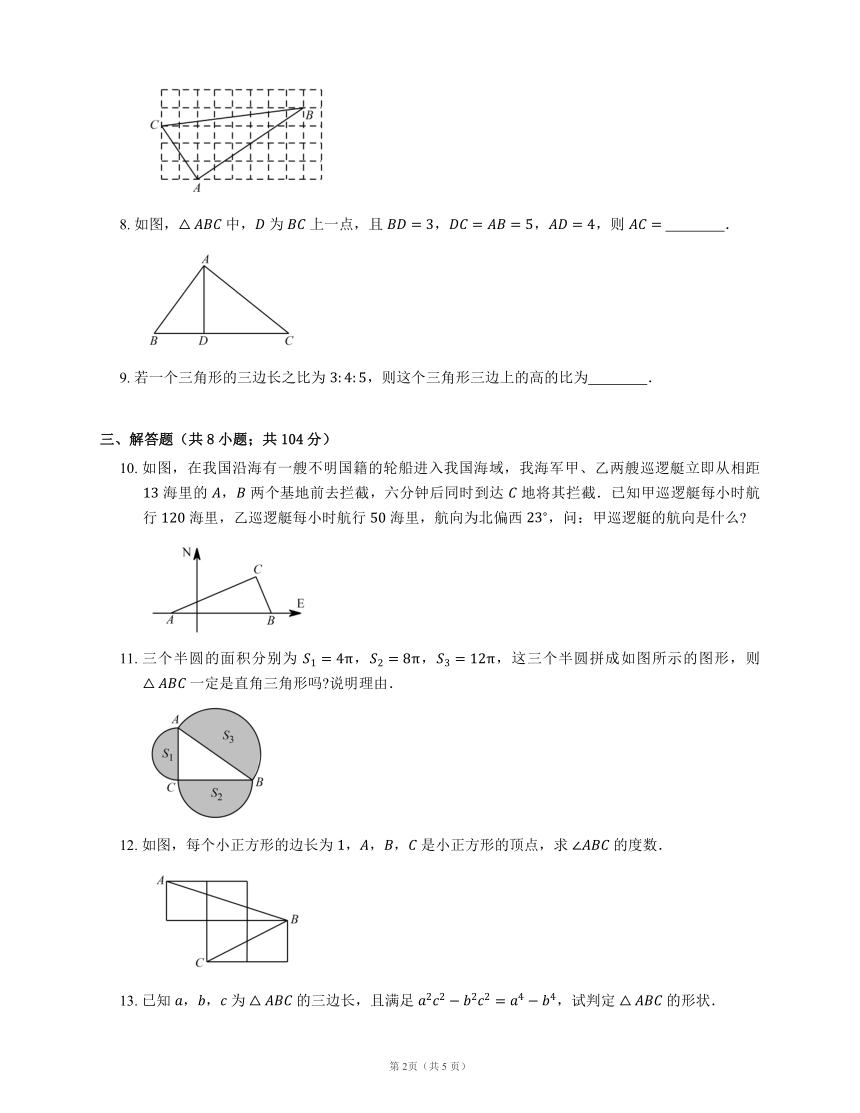
7. 如图, 的顶点均为正方形网格的格点,若每个小方格的边长均为 ,则 的形状是 .
8. 如图, 中, 为 上一点,且 ,,,则 .
9. 若一个三角形的三边长之比为 ,则这个三角形三边上的高的比为 .
三、解答题(共8小题;共104分)
10. 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距 海里的 , 两个基地前去拦截,六分钟后同时到达 地将其拦截.已知甲巡逻艇每小时航行 海里,乙巡逻艇每小时航行 海里,航向为北偏西 ,问:甲巡逻艇的航向是什么
11. 三个半圆的面积分别为 ,,,这三个半圆拼成如图所示的图形,则 一定是直角三角形吗 说明理由.
12. 如图,每个小正方形的边长为 ,,, 是小正方形的顶点,求 的度数.
13. 已知 ,, 为 的三边长,且满足 ,试判定 的形状.
14. 如图,某住宅小区在施工过程中留下了一块空地(图中的四边形 ),经测量,在四边形 中,,,,,.
(1) 是直角三角形 为什么
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米 元,则铺满这块空地共需花费多少元
15. 设一个直角三角形的两条直角边长为 ,,斜边上的高为 ,斜边长为 ,试判断以 ,, 为边长的三角形的形状.
16. 如图所示,在 中,,且周长为 ,点 从点 开始沿 边向 点以每秒 的速度移动;点 从点 开始沿 边向点 以每秒 的速度移动,如果 , 两点同时出发,问过 时, 的面积为多少
17. 张老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别观察 ,, 与 之间的关系,并用含自然数 的代数式表示: ; ; .
(2)猜想:以 ,, 为边长的三角形是否是直角三角形 为什么
答案
第一部分
1. C
2. D
3. C
第二部分
4. ②③
5. ,,
6. 不垂直
7. 直角三角形
8.
9.
第三部分
10. (海里),
(海里),
,
是直角三角形.
甲的航向为北偏东 .
11. 一定是直角三角形.理由如下:
,
所以 .
同理可求出 ,,
所以 ,
所以 一定是直角三角形.
12. ,, ,
,
是等腰直角三角形.
.
13. ,
,
得 或 ,或 且 ,
为直角三角形或等腰三角形或等腰直角三角形.
14. (1) 是直角三角形.
连接 .
,, ,
.
,,
.
是直角三角形.
(2) ,
铺满这块空地共需花费 元.
15. , ,
而
以 ,, 为边长的三角形是直角三角形.
16. ,且周长为 ,
,,, ,
为直角三角形.
过 时,, ,
的面积为 .
17. (1) ;;.
(2) 以 ,, 为边长的三角形是直角三角形.
理由:,
,
,
以 ,, 为边长的三角形是直角三角形.
第1页(共1 页)
一、选择题(共3小题;共15分)
1. 下列几组数中,为勾股数的是
A. ,, B. ,, C. ,, D. ,,
2. 一辆汽车从点 出发沿正东方向行驶 到达点 ,然后转向行驶 到达点 ,最后从点 沿 方向直接回到出发点 .如果汽车从出发到返回共行驶了 ,那么 的方向是
A. 正东或正西 B. 正南 C. 正北 D. 正南或正北
3. 有五根小木棒,其长度分别为 ,,,,,现将他们摆成两个直角三角形,其中正确的是
A. B.
C. D.
二、填空题(共6小题;共30分)
4. 下列 组数:① ,,;② ,,;③ ,,;④ ,,.其中是勾股数的为 (填序号).
5. 观察以下几组勾股数,并寻找规律:
① ,,;② ,,;③ ,,;④ ,,; 请你写出有以上规律的第⑤组勾股数: .
6. 一根电线杆高 ,为了安全起见,在电线杆顶部到与电线杆底部水平距离 处加一拉线.拉线工人发现所用线长为 米(不计捆缚部分),则电线杆与地面 (填“垂直”或“不垂直”).
7. 如图, 的顶点均为正方形网格的格点,若每个小方格的边长均为 ,则 的形状是 .
8. 如图, 中, 为 上一点,且 ,,,则 .
9. 若一个三角形的三边长之比为 ,则这个三角形三边上的高的比为 .
三、解答题(共8小题;共104分)
10. 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距 海里的 , 两个基地前去拦截,六分钟后同时到达 地将其拦截.已知甲巡逻艇每小时航行 海里,乙巡逻艇每小时航行 海里,航向为北偏西 ,问:甲巡逻艇的航向是什么
11. 三个半圆的面积分别为 ,,,这三个半圆拼成如图所示的图形,则 一定是直角三角形吗 说明理由.
12. 如图,每个小正方形的边长为 ,,, 是小正方形的顶点,求 的度数.
13. 已知 ,, 为 的三边长,且满足 ,试判定 的形状.
14. 如图,某住宅小区在施工过程中留下了一块空地(图中的四边形 ),经测量,在四边形 中,,,,,.
(1) 是直角三角形 为什么
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米 元,则铺满这块空地共需花费多少元
15. 设一个直角三角形的两条直角边长为 ,,斜边上的高为 ,斜边长为 ,试判断以 ,, 为边长的三角形的形状.
16. 如图所示,在 中,,且周长为 ,点 从点 开始沿 边向 点以每秒 的速度移动;点 从点 开始沿 边向点 以每秒 的速度移动,如果 , 两点同时出发,问过 时, 的面积为多少
17. 张老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别观察 ,, 与 之间的关系,并用含自然数 的代数式表示: ; ; .
(2)猜想:以 ,, 为边长的三角形是否是直角三角形 为什么
答案
第一部分
1. C
2. D
3. C
第二部分
4. ②③
5. ,,
6. 不垂直
7. 直角三角形
8.
9.
第三部分
10. (海里),
(海里),
,
是直角三角形.
甲的航向为北偏东 .
11. 一定是直角三角形.理由如下:
,
所以 .
同理可求出 ,,
所以 ,
所以 一定是直角三角形.
12. ,, ,
,
是等腰直角三角形.
.
13. ,
,
得 或 ,或 且 ,
为直角三角形或等腰三角形或等腰直角三角形.
14. (1) 是直角三角形.
连接 .
,, ,
.
,,
.
是直角三角形.
(2) ,
铺满这块空地共需花费 元.
15. , ,
而
以 ,, 为边长的三角形是直角三角形.
16. ,且周长为 ,
,,, ,
为直角三角形.
过 时,, ,
的面积为 .
17. (1) ;;.
(2) 以 ,, 为边长的三角形是直角三角形.
理由:,
,
,
以 ,, 为边长的三角形是直角三角形.
第1页(共1 页)
