北师大版八年级上册5.8三元一次方程组同步练习(word版含解析)
文档属性
| 名称 | 北师大版八年级上册5.8三元一次方程组同步练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 156.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-11 07:44:35 | ||
图片预览


文档简介
北师大版同步检测卷:三元一次方程组
一、选择题(共10小题;共50分)
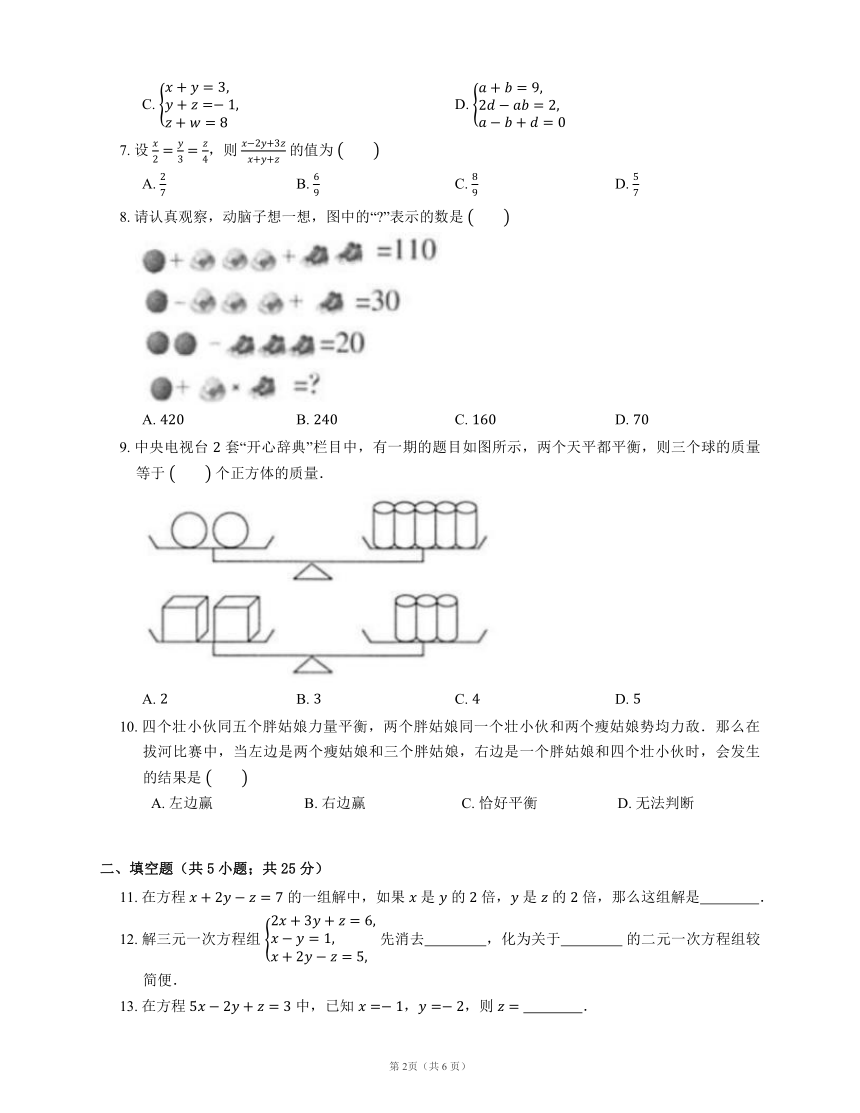
1. 有三种不同质量的物体“”“”“”,其中,同一种物体的质量都相等.现左右手中同样的盘子上都放着不同个数的物体,只有一组左右质量不相等,则该组是
A. B.
C. D.
2. 下列方程组不是三元一次方程组的是
A. B.
C. D.
3. 为确保信息安全,信息需加密传输,发送方由明文 密文(加密);接收方由密文 明文(解密).已知加密规则为明文 ,,, 对应密文 ,,,.例如:明文 ,,, 对应密文 ,,,.当接收方收到密文 ,,, 时,解密得到的明文为
A. ,,, B. ,,, C. ,,, D. ,,,
4. 下列方程组中,是三元一次方程组的是
A. B.
C. D.
5. 三元一次方程组 的解是
A. B. C. D.
6. 下列方程组中,为三元一次方程组的是
A. B.
C. D.
7. 设 ,则 的值为
A. B. C. D.
8. 请认真观察,动脑子想一想,图中的“ ”表示的数是
A. B. C. D.
9. 中央电视台 套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则三个球的质量等于 个正方体的质量.
A. B. C. D.
10. 四个壮小伙同五个胖姑娘力量平衡,两个胖姑娘同一个壮小伙和两个瘦姑娘势均力敌.那么在拔河比赛中,当左边是两个瘦姑娘和三个胖姑娘,右边是一个胖姑娘和四个壮小伙时,会发生的结果是
A. 左边赢 B. 右边赢 C. 恰好平衡 D. 无法判断
二、填空题(共5小题;共25分)
11. 在方程 的一组解中,如果 是 的 倍, 是 的 倍,那么这组解是 .
12. 解三元一次方程组 先消去 ,化为关于 的二元一次方程组较简便.
13. 在方程 中,已知 ,,则 .
14. 若 是一个关于 ,, 的三元一次方程,则 , .
15. 一笔总额为 元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍.若把这笔奖金发给 个人,评一、二、三等奖的人数分别为 ,,,且 ,那么三等奖的奖金金额是 元.
三、解答题(共3小题;共39分)
16. 某单位职工在植树节时去植树,甲、乙、丙三个小组共植树 棵,乙组植树的棵数是甲、丙两组的和的 ,甲组植树的棵数恰是乙组与丙组的和,求每组各植树多少棵.
17. 下列方程组中,哪些是三元一次方程组
(1)
(2)
(3)
18. 解方程组:
答案
第一部分
1. A 【解析】设的质量为 ,的质量为 ,的质量为 ,
观察 个选项可知,选项A中,,而选项D中,,显然A和D中有一个选项是符合题意的,
而选项B,C都是不符合题意的,
选项B中,,可得 ,
选项C中,,可得 ,
故A选项符合题意.
2. D 【解析】选项D的 中 的次数是 ,故D中方程组不符合三元一次方程组的定义.故D中的方程组不是三元一次方程组.
3. C 【解析】由题意得 解得
4. C 【解析】A选项中含有四个未知数,B选项中项 的次数是 ,D选项中 这一项不是整式.故选C.
5. C
【解析】,
,,
把 , 代入 ,得 ,解得 ,
把 分别代入 ,,得 ,,
方程组的解为
6. B 【解析】 A选项和C选项中都有四个未知数,而D选项中含未知数的项的最高次数是 ,
选项A,C,D 都不是三元一次方程组,
故选B.
7. C 【解析】设 ,则 ,,,
.
8. B 【解析】设题图中一个篮球表示的数是 ,一顶帽子表示的数是 ,一双鞋表示的数是 ,
依题意得
① ②得
③ ④得 ,解得 ,
把 代入③得 ,解得 ,
把 , 代入①得 ,解得 ,
则方程组的解为
故 .
9. D 【解析】设一个球的质量为 ,一个圆柱的质量为 ,一个正方体的质量为 ,
则根据等量关系可列方程组为
消去 可得 ,则 ,
即三个球的质量等于五个正方体的质量.
故选D.
10. B
【解析】设一个胖姑娘的力量是 ,一个瘦姑娘的力量是 ,一个壮小伙的力量是 ,
则 ,两个瘦姑娘和三个胖姑娘的力量是 ,一个胖姑娘和四个壮小伙的力量是 ,
根据题意得
② ①得 ,整理得 ,
,
右边赢.
第二部分
11.
12. ,,
13.
14. ,
【解析】由题意可得 ,,,
,.
15. 或
【解析】,,且 ,, 均为整数,
或 或
设三等奖的奖金金额为 元,
则二等奖的奖金金额为 元,一等奖的奖金金额为 元,
依题意,得 或 或 ,
解得 (不合题意,舍去)或 或 .
第三部分
16. 设甲组植树 棵,乙组植树 棵,丙组植树 棵,根据题意,得
解得
答:甲组植树 棵,乙组植树 棵,丙组植树 棵.
17. (1) 是.
(2) 不是.
(3) 是.
18. 把③代入①得
把③代入②得
④ ⑤得
解得
把 代入④得
解得
把 代入③得
故原方程组的解为
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 有三种不同质量的物体“”“”“”,其中,同一种物体的质量都相等.现左右手中同样的盘子上都放着不同个数的物体,只有一组左右质量不相等,则该组是
A. B.
C. D.
2. 下列方程组不是三元一次方程组的是
A. B.
C. D.
3. 为确保信息安全,信息需加密传输,发送方由明文 密文(加密);接收方由密文 明文(解密).已知加密规则为明文 ,,, 对应密文 ,,,.例如:明文 ,,, 对应密文 ,,,.当接收方收到密文 ,,, 时,解密得到的明文为
A. ,,, B. ,,, C. ,,, D. ,,,
4. 下列方程组中,是三元一次方程组的是
A. B.
C. D.
5. 三元一次方程组 的解是
A. B. C. D.
6. 下列方程组中,为三元一次方程组的是
A. B.
C. D.
7. 设 ,则 的值为
A. B. C. D.
8. 请认真观察,动脑子想一想,图中的“ ”表示的数是
A. B. C. D.
9. 中央电视台 套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则三个球的质量等于 个正方体的质量.
A. B. C. D.
10. 四个壮小伙同五个胖姑娘力量平衡,两个胖姑娘同一个壮小伙和两个瘦姑娘势均力敌.那么在拔河比赛中,当左边是两个瘦姑娘和三个胖姑娘,右边是一个胖姑娘和四个壮小伙时,会发生的结果是
A. 左边赢 B. 右边赢 C. 恰好平衡 D. 无法判断
二、填空题(共5小题;共25分)
11. 在方程 的一组解中,如果 是 的 倍, 是 的 倍,那么这组解是 .
12. 解三元一次方程组 先消去 ,化为关于 的二元一次方程组较简便.
13. 在方程 中,已知 ,,则 .
14. 若 是一个关于 ,, 的三元一次方程,则 , .
15. 一笔总额为 元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍.若把这笔奖金发给 个人,评一、二、三等奖的人数分别为 ,,,且 ,那么三等奖的奖金金额是 元.
三、解答题(共3小题;共39分)
16. 某单位职工在植树节时去植树,甲、乙、丙三个小组共植树 棵,乙组植树的棵数是甲、丙两组的和的 ,甲组植树的棵数恰是乙组与丙组的和,求每组各植树多少棵.
17. 下列方程组中,哪些是三元一次方程组
(1)
(2)
(3)
18. 解方程组:
答案
第一部分
1. A 【解析】设的质量为 ,的质量为 ,的质量为 ,
观察 个选项可知,选项A中,,而选项D中,,显然A和D中有一个选项是符合题意的,
而选项B,C都是不符合题意的,
选项B中,,可得 ,
选项C中,,可得 ,
故A选项符合题意.
2. D 【解析】选项D的 中 的次数是 ,故D中方程组不符合三元一次方程组的定义.故D中的方程组不是三元一次方程组.
3. C 【解析】由题意得 解得
4. C 【解析】A选项中含有四个未知数,B选项中项 的次数是 ,D选项中 这一项不是整式.故选C.
5. C
【解析】,
,,
把 , 代入 ,得 ,解得 ,
把 分别代入 ,,得 ,,
方程组的解为
6. B 【解析】 A选项和C选项中都有四个未知数,而D选项中含未知数的项的最高次数是 ,
选项A,C,D 都不是三元一次方程组,
故选B.
7. C 【解析】设 ,则 ,,,
.
8. B 【解析】设题图中一个篮球表示的数是 ,一顶帽子表示的数是 ,一双鞋表示的数是 ,
依题意得
① ②得
③ ④得 ,解得 ,
把 代入③得 ,解得 ,
把 , 代入①得 ,解得 ,
则方程组的解为
故 .
9. D 【解析】设一个球的质量为 ,一个圆柱的质量为 ,一个正方体的质量为 ,
则根据等量关系可列方程组为
消去 可得 ,则 ,
即三个球的质量等于五个正方体的质量.
故选D.
10. B
【解析】设一个胖姑娘的力量是 ,一个瘦姑娘的力量是 ,一个壮小伙的力量是 ,
则 ,两个瘦姑娘和三个胖姑娘的力量是 ,一个胖姑娘和四个壮小伙的力量是 ,
根据题意得
② ①得 ,整理得 ,
,
右边赢.
第二部分
11.
12. ,,
13.
14. ,
【解析】由题意可得 ,,,
,.
15. 或
【解析】,,且 ,, 均为整数,
或 或
设三等奖的奖金金额为 元,
则二等奖的奖金金额为 元,一等奖的奖金金额为 元,
依题意,得 或 或 ,
解得 (不合题意,舍去)或 或 .
第三部分
16. 设甲组植树 棵,乙组植树 棵,丙组植树 棵,根据题意,得
解得
答:甲组植树 棵,乙组植树 棵,丙组植树 棵.
17. (1) 是.
(2) 不是.
(3) 是.
18. 把③代入①得
把③代入②得
④ ⑤得
解得
把 代入④得
解得
把 代入③得
故原方程组的解为
第1页(共1 页)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
