2021-2022学年北师大版九年级数学上册第六章反比例函数期末章节总复习2(Word版,含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册第六章反比例函数期末章节总复习2(Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 743.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览




文档简介
北师大版九年级数学上学期期末章节总复习 第六章 反比例函数 2021中考真题专训2
姓名:___________班级:___________
一、单选题
1.(2021·广西梧州·中考真题)如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1,y2的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A.5t B. C. D.5
2.(2021·湖北天门·中考真题)下列说法正确的是( )
A.函数的图象是过原点的射线 B.直线经过第一 二 三象限
C.函数,y随x增大而增大 D.函数,y随x增大而减小
3.(2021·辽宁阜新·中考真题)已知点,都在反比例函数的图象上,且,则,的关系是( )
A. B. C. D.
4.(2021·山东济南·中考真题)反比例函数图象的两个分支分别位于第一、三象限,则一次函数的图象大致是( )
A.B.C. D.
5.(2021·山西·中考真题)已知反比例函数,则下列描述不正确的是( )
A.图象位于第一,第三象限 B.图象必经过点
C.图象不可能与坐标轴相交 D.随的增大而减小
6.(2021·贵州遵义·中考真题)已知反比例函数y(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
7.(2021·浙江嘉兴·中考真题)已知三个点,,在反比例函数的图象上,其中,下列结论中正确的是( )
A. B. C. D.
8.(2021·甘肃兰州·中考真题)如图,点在反比例函数图象上,轴于点,是的中点,连接,,若的面积为2,则( )
A.4 B.8 C.12 D.16
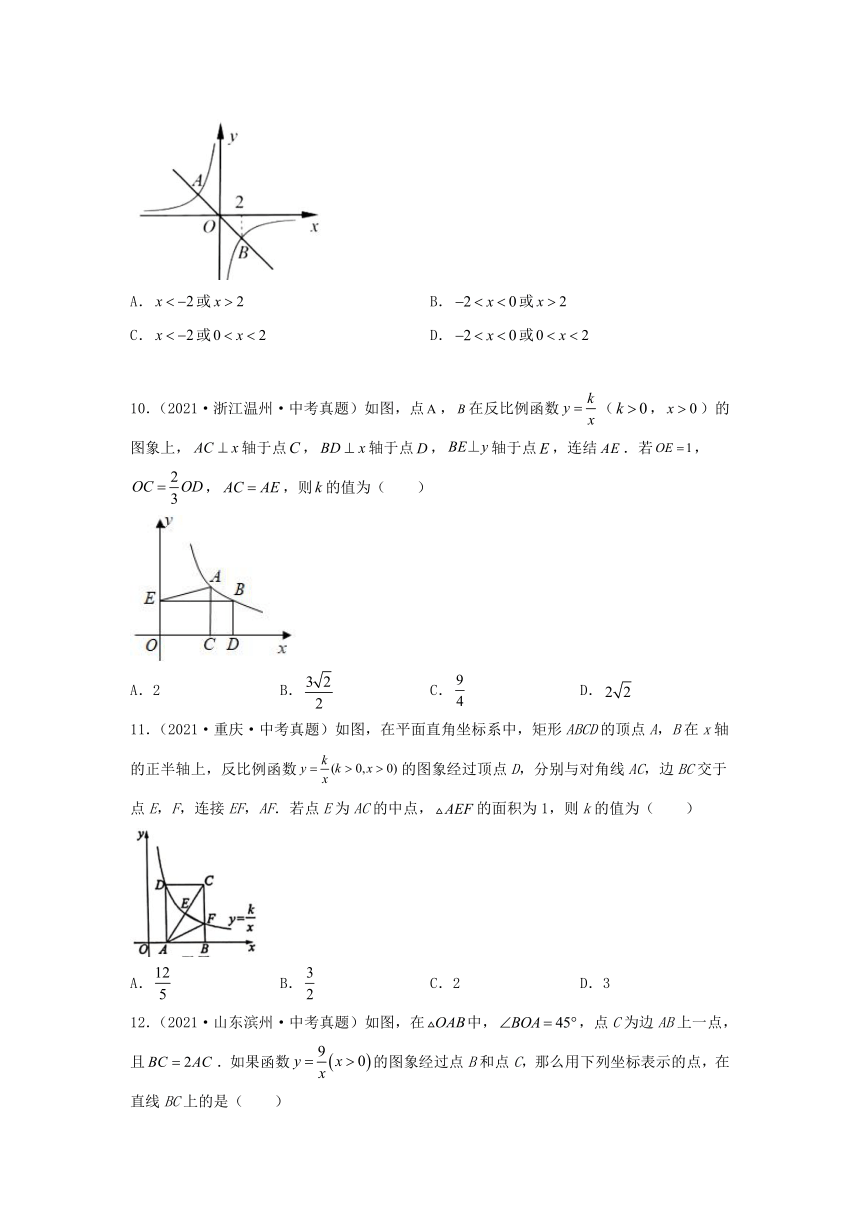
9.(2021·浙江宁波·中考真题)如图,正比例函数的图象与反比例函数的图象相交于A,B两点,点B的横坐标为2,当时,x的取值范围是( )
A.或 B.或
C.或 D.或
10.(2021·浙江温州·中考真题)如图,点,在反比例函数(,)的图象上,轴于点,轴于点,轴于点,连结.若,,,则的值为( )
A.2 B. C. D.
11.(2021·重庆·中考真题)如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,的面积为1,则k的值为( )
A. B. C.2 D.3
12.(2021·山东滨州·中考真题)如图,在中,,点C为边AB上一点,且.如果函数的图象经过点B和点C,那么用下列坐标表示的点,在直线BC上的是( )
A.(-2019,674) B.(-2020,675)
C.(2021,-669) D.(2022,-670)
二、填空题
13.(2021·陕西·中考真题)若,是反比例函数图象上的两点,则、的大小关系是______(填“>”、“=”或“<”)
14.(2021·黑龙江牡丹江·中考真题)在函数y=中,自变量x的取值范围是_____.
15.(2021·湖南永州·中考真题)写出一个图象位于第二、第四象限的反比例函数的解析式________.
16.(2021·云南·中考真题)若反比例函数的图象经过点,则该反比例函数的解析式(解析式也称表达式)为_________.
17.(2021·北京·中考真题)在平面直角坐标系中,若反比例函数的图象经过点和点,则的值为______________.
18.(2021·江苏徐州·中考真题)如图,点分别在函数的图像上,点在轴上.若四边形为正方形,点在第一象限,则的坐标是_____________.
19.(2021·湖北鄂州·中考真题)如图,点是反比例函数的图象上一点,过点作轴于点,交反比例函数的图象于点,点是轴正半轴上一点.若的面积为2,则的值为_____________.
20.(2021·山东滨州·中考真题)若点、、都在反比例函数(k为常数)的图象上,则、、的大小关系为____________.
三、解答题
21.(2021·四川宜宾·中考真题)如图,一次函数y=ax+b的图象与反比例函数的图象交于点A、B,与x轴交于点,若OC=AC,且=10
(1)求反比例函数与一次函数的表达式;
(2)请直接写出不等式ax+b>的解集.
22.(2021·浙江杭州·中考真题)在直角坐标系中,设函数(是常数,,)与函数(是常数,)的图象交于点A,点A关于轴的对称点为点.
(1)若点的坐标为,
①求,的值.
②当时,直接写出的取值范围.
(2)若点在函数(是常数,)的图象上,求的值.
23.(2021·新疆·中考真题)如图,一次函数与反比例函数的图象交于点,.
(1)求反比例函数和一次函数的解析式;
(2)判断点是否在一次函数的图象上,并说明理由;
(3)直接写出不等式的解集.
24.(2021·湖南岳阳·中考真题)如图,已知反比例函数与正比例函数的图象交于,两点.
(1)求该反比例函数的表达式;
(2)若点在轴上,且的面积为3,求点的坐标.
25.(2021·广东·中考真题)在平面直角坐标系中,一次函数的图象与x轴、y轴分别交于A、B两点,且与反比例函数图象的一个交点为.
(1)求m的值;
(2)若,求k的值.
26.(2021·四川阿坝·中考真题)如图,一次函数的图象与反比例函数的图象相交于和B两点.
(1)求反比例函数的解析式;
(2)求点B的坐标.
27.(2021·甘肃兰州·中考真题)如图,一次函数与反比例函数,图象分别交于,,与轴交于点,连接,.
(1)求反比例函数和一次函数的表达式;
(2)求的面积.
28.(2021·四川乐山·中考真题)如图,直线分别交轴,轴于、两点,交反比例函数的图象于、两点.若,且的面积为4
(1)求的值;
(2)当点的横坐标为时,求的面积.
29.(2021·四川广安·中考真题)如图,一次函数的图象与反比例函数的图象交于,两点.
(1)求一次函数和反比例函数的解析式;
(2)点在轴上,且满足的面积等于4,请直接写出点的坐标.
30.(2021·四川成都·中考真题)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点,与x轴相交于点B.
(1)求反比例函数的表达式;
过点A的直线交反比例函数的图象于另一点C,交x轴正半轴于点D,当是以为底的等腰三角形时,求直线的函数表达式及点C的坐标.
参考答案
1.C 2.C 3.A 4.D 5.D 6.C 7.A 8.B 9.C 10.B 11.D 12.D
13.< 14.. 15.(答案不唯一) 16. 17. 18.(2,3)
19.8 20.
21.
(1)过点A作轴于点D
,OC=AC,=10
代入,
把,代入y=ax+b,得:
,解得
(2)联立
解得:
或(A点坐标)
ax+b>的解集,即图像中一次函数的值大于反比例函数的值.
.
22.
解(1)①由题意得,点A的坐标是,
因为函数的图象过点A,
所以,
同理.
②由图象可知,当时,反比例函数的图象位于正比例函数图象的下方,
即当时,.
(2)设点A的坐标是,则点的坐标是,
所以,,
所以.
23.
解:(1)将点代入反比例函数中,得,
∴反比例函数解析式为;
将点代入,得-a=6,
∴a=-6,
∴,
将点、代入一次函数中,得
,∴,
∴一次函数的解析式为;
(2)点P在一次函数的图象上.
理由:当x=-2时,,
∴点P在一次函数的图象上;
(3)由图象可知:当或时,一次函数的图象在反比例函数图象的上方,即,
∴当或时.
24.
解:(1)将点坐标代入中可得:,
∴;
将代入可得:,
∴该反比例函数的表达式为;
(2)因为该反比例函数的图像和一次函数的图像交于,两点,
∴,两点关于原点对称,
∴,
∴B点到OC的距离为2,
∵的面积为3,
∴,
∴,
当C点在O点左侧时,;
当C点在O点右侧时,;
∴点的坐标为或.
25.
解:(1)∵P为反比例函数上一点,
∴代入得,
∴.
(2)令,即,
∴,,
令,∴,
∵.
由图象得,可分为以下两种情况,
①B在y轴正半轴时,,
∵,
过P作轴交x轴于点H,又,,
∴
∴, ,
即 ,
∴,
∴,
∴.
②B在y轴负半轴时,,过P作轴,
∵,
∴,
∴,
∴,
,
∵ ,
∴,代入
∴,
综上,或.
26.
解:(1)将代入一次函数中得:
,
∴,代入反比例函数中得:,
解得:k=4,
∴反比例函数解析式为;
(2)联立一次函数与反比例函数解析式得:
解得:或,
∴.
27.
解:(1)∵,在函数的图象上,
∴m=5,
∴A(-2,5),
把A(-2,5)代入得:,
∴b=4,
∴一次函数的表达式为:,
∵在函数的图象上,
∴n=2,
∴,
把代入得:2=,∴k=8,
∴反比例函数的解析式为:;
(2)∵C是直线AB与y轴的交点,直线AB:,
∴当x=0时,y=4,
∴点C(0,4),即OC=4,
∵A(-2,5),,
∴=×4×2+×4×4=12;
28.
(1)过作垂直于轴,垂足为,
∴,
∴.
∵,,
∴,,
∴,.
∴,,即.
(2)由(1)知,∴.
∵,∴,∴,.
设直线的解析式为,
将点、代入,得.
解得.
∴直线的解析式为.
联立方程组,解得,,
∴.
∴.
29.
解:(1)由题意可得:
点B(3,-2)在反比例函数图像上,
∴,则m=-6,
∴反比例函数的解析式为,
将A(-1,n)代入,
得:,即A(-1,6),
将A,B代入一次函数解析式中,得
,解得:,
∴一次函数解析式为;
(2)∵点P在x轴上,
设点P的坐标为(a,0),
∵一次函数解析式为,令y=0,则x=2,
∴直线AB与x轴交于点(2,0),
由△ABP的面积为4,可得:
,即,
解得:a=1或a=3,
∴点P的坐标为(1,0)或(3,0).
30.
(1)将点的坐标代入一次函数表达式并解得:a=2,
故,
将点A的坐标代入反比例函数表达式并解得:k=6,
故反比例函数表达式为:y(x>0) ;
(2)∵
∴
∵是以为底的等腰三角形,
∴
设一次函数AD的表达式为:y=kx+b
得:
解得:
∴解析式为:
联立反比例函数和直线AD的解析式得
解得(舍去)或
∴点C的坐标为.
姓名:___________班级:___________
一、单选题
1.(2021·广西梧州·中考真题)如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1,y2的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A.5t B. C. D.5
2.(2021·湖北天门·中考真题)下列说法正确的是( )
A.函数的图象是过原点的射线 B.直线经过第一 二 三象限
C.函数,y随x增大而增大 D.函数,y随x增大而减小
3.(2021·辽宁阜新·中考真题)已知点,都在反比例函数的图象上,且,则,的关系是( )
A. B. C. D.
4.(2021·山东济南·中考真题)反比例函数图象的两个分支分别位于第一、三象限,则一次函数的图象大致是( )
A.B.C. D.
5.(2021·山西·中考真题)已知反比例函数,则下列描述不正确的是( )
A.图象位于第一,第三象限 B.图象必经过点
C.图象不可能与坐标轴相交 D.随的增大而减小
6.(2021·贵州遵义·中考真题)已知反比例函数y(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
7.(2021·浙江嘉兴·中考真题)已知三个点,,在反比例函数的图象上,其中,下列结论中正确的是( )
A. B. C. D.
8.(2021·甘肃兰州·中考真题)如图,点在反比例函数图象上,轴于点,是的中点,连接,,若的面积为2,则( )
A.4 B.8 C.12 D.16
9.(2021·浙江宁波·中考真题)如图,正比例函数的图象与反比例函数的图象相交于A,B两点,点B的横坐标为2,当时,x的取值范围是( )
A.或 B.或
C.或 D.或
10.(2021·浙江温州·中考真题)如图,点,在反比例函数(,)的图象上,轴于点,轴于点,轴于点,连结.若,,,则的值为( )
A.2 B. C. D.
11.(2021·重庆·中考真题)如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,的面积为1,则k的值为( )
A. B. C.2 D.3
12.(2021·山东滨州·中考真题)如图,在中,,点C为边AB上一点,且.如果函数的图象经过点B和点C,那么用下列坐标表示的点,在直线BC上的是( )
A.(-2019,674) B.(-2020,675)
C.(2021,-669) D.(2022,-670)
二、填空题
13.(2021·陕西·中考真题)若,是反比例函数图象上的两点,则、的大小关系是______(填“>”、“=”或“<”)
14.(2021·黑龙江牡丹江·中考真题)在函数y=中,自变量x的取值范围是_____.
15.(2021·湖南永州·中考真题)写出一个图象位于第二、第四象限的反比例函数的解析式________.
16.(2021·云南·中考真题)若反比例函数的图象经过点,则该反比例函数的解析式(解析式也称表达式)为_________.
17.(2021·北京·中考真题)在平面直角坐标系中,若反比例函数的图象经过点和点,则的值为______________.
18.(2021·江苏徐州·中考真题)如图,点分别在函数的图像上,点在轴上.若四边形为正方形,点在第一象限,则的坐标是_____________.
19.(2021·湖北鄂州·中考真题)如图,点是反比例函数的图象上一点,过点作轴于点,交反比例函数的图象于点,点是轴正半轴上一点.若的面积为2,则的值为_____________.
20.(2021·山东滨州·中考真题)若点、、都在反比例函数(k为常数)的图象上,则、、的大小关系为____________.
三、解答题
21.(2021·四川宜宾·中考真题)如图,一次函数y=ax+b的图象与反比例函数的图象交于点A、B,与x轴交于点,若OC=AC,且=10
(1)求反比例函数与一次函数的表达式;
(2)请直接写出不等式ax+b>的解集.
22.(2021·浙江杭州·中考真题)在直角坐标系中,设函数(是常数,,)与函数(是常数,)的图象交于点A,点A关于轴的对称点为点.
(1)若点的坐标为,
①求,的值.
②当时,直接写出的取值范围.
(2)若点在函数(是常数,)的图象上,求的值.
23.(2021·新疆·中考真题)如图,一次函数与反比例函数的图象交于点,.
(1)求反比例函数和一次函数的解析式;
(2)判断点是否在一次函数的图象上,并说明理由;
(3)直接写出不等式的解集.
24.(2021·湖南岳阳·中考真题)如图,已知反比例函数与正比例函数的图象交于,两点.
(1)求该反比例函数的表达式;
(2)若点在轴上,且的面积为3,求点的坐标.
25.(2021·广东·中考真题)在平面直角坐标系中,一次函数的图象与x轴、y轴分别交于A、B两点,且与反比例函数图象的一个交点为.
(1)求m的值;
(2)若,求k的值.
26.(2021·四川阿坝·中考真题)如图,一次函数的图象与反比例函数的图象相交于和B两点.
(1)求反比例函数的解析式;
(2)求点B的坐标.
27.(2021·甘肃兰州·中考真题)如图,一次函数与反比例函数,图象分别交于,,与轴交于点,连接,.
(1)求反比例函数和一次函数的表达式;
(2)求的面积.
28.(2021·四川乐山·中考真题)如图,直线分别交轴,轴于、两点,交反比例函数的图象于、两点.若,且的面积为4
(1)求的值;
(2)当点的横坐标为时,求的面积.
29.(2021·四川广安·中考真题)如图,一次函数的图象与反比例函数的图象交于,两点.
(1)求一次函数和反比例函数的解析式;
(2)点在轴上,且满足的面积等于4,请直接写出点的坐标.
30.(2021·四川成都·中考真题)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点,与x轴相交于点B.
(1)求反比例函数的表达式;
过点A的直线交反比例函数的图象于另一点C,交x轴正半轴于点D,当是以为底的等腰三角形时,求直线的函数表达式及点C的坐标.
参考答案
1.C 2.C 3.A 4.D 5.D 6.C 7.A 8.B 9.C 10.B 11.D 12.D
13.< 14.. 15.(答案不唯一) 16. 17. 18.(2,3)
19.8 20.
21.
(1)过点A作轴于点D
,OC=AC,=10
代入,
把,代入y=ax+b,得:
,解得
(2)联立
解得:
或(A点坐标)
ax+b>的解集,即图像中一次函数的值大于反比例函数的值.
.
22.
解(1)①由题意得,点A的坐标是,
因为函数的图象过点A,
所以,
同理.
②由图象可知,当时,反比例函数的图象位于正比例函数图象的下方,
即当时,.
(2)设点A的坐标是,则点的坐标是,
所以,,
所以.
23.
解:(1)将点代入反比例函数中,得,
∴反比例函数解析式为;
将点代入,得-a=6,
∴a=-6,
∴,
将点、代入一次函数中,得
,∴,
∴一次函数的解析式为;
(2)点P在一次函数的图象上.
理由:当x=-2时,,
∴点P在一次函数的图象上;
(3)由图象可知:当或时,一次函数的图象在反比例函数图象的上方,即,
∴当或时.
24.
解:(1)将点坐标代入中可得:,
∴;
将代入可得:,
∴该反比例函数的表达式为;
(2)因为该反比例函数的图像和一次函数的图像交于,两点,
∴,两点关于原点对称,
∴,
∴B点到OC的距离为2,
∵的面积为3,
∴,
∴,
当C点在O点左侧时,;
当C点在O点右侧时,;
∴点的坐标为或.
25.
解:(1)∵P为反比例函数上一点,
∴代入得,
∴.
(2)令,即,
∴,,
令,∴,
∵.
由图象得,可分为以下两种情况,
①B在y轴正半轴时,,
∵,
过P作轴交x轴于点H,又,,
∴
∴, ,
即 ,
∴,
∴,
∴.
②B在y轴负半轴时,,过P作轴,
∵,
∴,
∴,
∴,
,
∵ ,
∴,代入
∴,
综上,或.
26.
解:(1)将代入一次函数中得:
,
∴,代入反比例函数中得:,
解得:k=4,
∴反比例函数解析式为;
(2)联立一次函数与反比例函数解析式得:
解得:或,
∴.
27.
解:(1)∵,在函数的图象上,
∴m=5,
∴A(-2,5),
把A(-2,5)代入得:,
∴b=4,
∴一次函数的表达式为:,
∵在函数的图象上,
∴n=2,
∴,
把代入得:2=,∴k=8,
∴反比例函数的解析式为:;
(2)∵C是直线AB与y轴的交点,直线AB:,
∴当x=0时,y=4,
∴点C(0,4),即OC=4,
∵A(-2,5),,
∴=×4×2+×4×4=12;
28.
(1)过作垂直于轴,垂足为,
∴,
∴.
∵,,
∴,,
∴,.
∴,,即.
(2)由(1)知,∴.
∵,∴,∴,.
设直线的解析式为,
将点、代入,得.
解得.
∴直线的解析式为.
联立方程组,解得,,
∴.
∴.
29.
解:(1)由题意可得:
点B(3,-2)在反比例函数图像上,
∴,则m=-6,
∴反比例函数的解析式为,
将A(-1,n)代入,
得:,即A(-1,6),
将A,B代入一次函数解析式中,得
,解得:,
∴一次函数解析式为;
(2)∵点P在x轴上,
设点P的坐标为(a,0),
∵一次函数解析式为,令y=0,则x=2,
∴直线AB与x轴交于点(2,0),
由△ABP的面积为4,可得:
,即,
解得:a=1或a=3,
∴点P的坐标为(1,0)或(3,0).
30.
(1)将点的坐标代入一次函数表达式并解得:a=2,
故,
将点A的坐标代入反比例函数表达式并解得:k=6,
故反比例函数表达式为:y(x>0) ;
(2)∵
∴
∵是以为底的等腰三角形,
∴
设一次函数AD的表达式为:y=kx+b
得:
解得:
∴解析式为:
联立反比例函数和直线AD的解析式得
解得(舍去)或
∴点C的坐标为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
