2021-2022学年北师大版九年级数学上册第六章反比例函数期末章节总复习1(Word版,含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册第六章反比例函数期末章节总复习1(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 618.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 23:39:51 | ||
图片预览


文档简介
北师大版九年级数学上学期期末章节总复习 第六章 反比例函数 2021中考真题专训1
姓名:___________班级:___________
一、单选题
1.(2021·黑龙江大庆·中考真题)已知反比例函数,当时,随的增大而减小,那么一次的数的图像经过第( )
A.一,二,三象限 B.一,二,四象限
C.一,三,四象限 D.二,三,四象限
2.(2021·贵州安顺·中考真题)已知反比例函数的图象与正比例函数的图象相交于两点,若点的坐标是,则点的坐标是( )
A. B. C. D.
3.(2021·辽宁朝阳·中考真题)如图,O是坐标原点,点B在x轴上,在OAB中,AO=AB=5,OB=6,点A在反比例函数y=(k≠0)图象上,则k的值( )
A.﹣12 B.﹣15 C.﹣20 D.﹣30
4.(2021·江苏宿迁·中考真题)已知双曲线过点(3,)、(1,)、(-2,),则下列结论正确的是( )
A. B. C. D.
5.(2021·辽宁大连·中考真题)下列说法正确的是( )
①反比例函数中自变量x的取值范围是;
②点在反比例函数的图象上;
③反比例函数的图象,在每一个象限内,y随x的增大而增大.
A.①② B.①③ C.②③ D.①②③
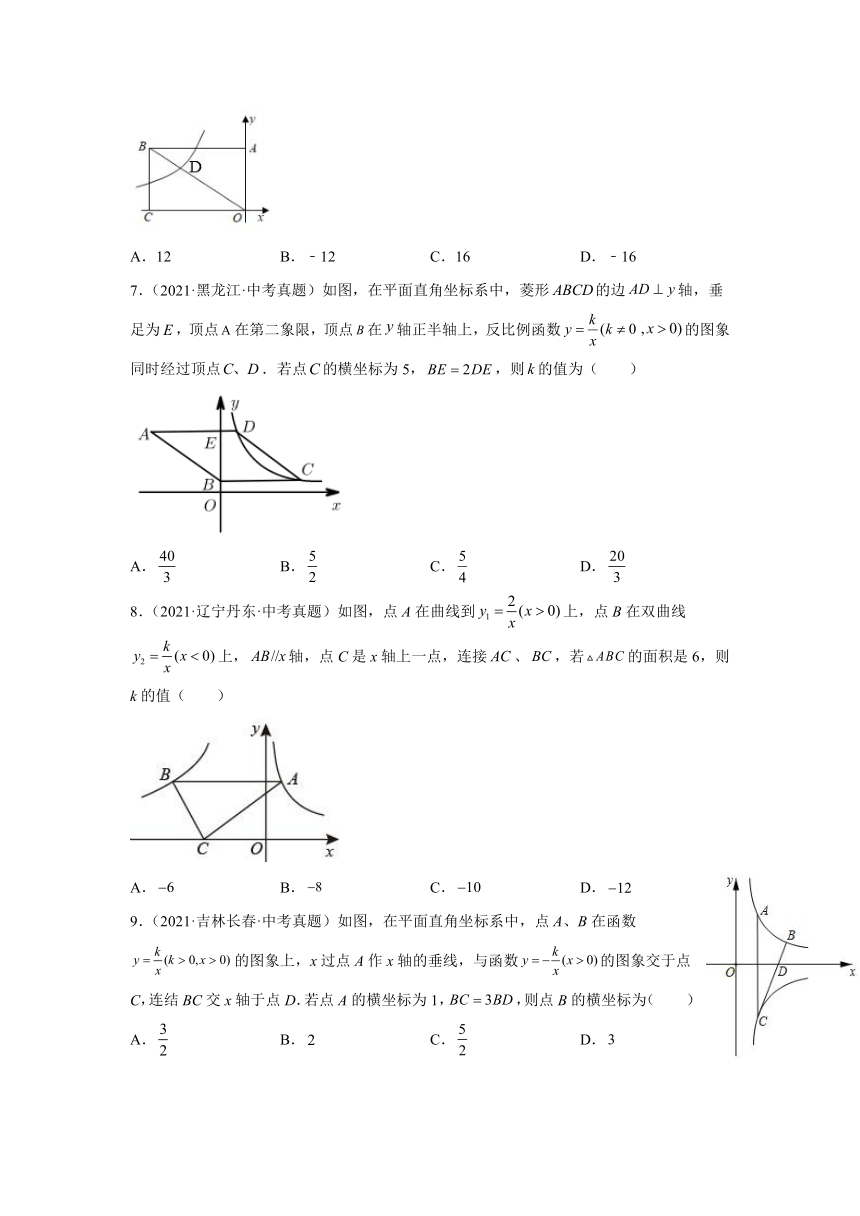
6.(2021·黑龙江牡丹江·中考真题)如图,矩形OABC的面积为36,它的对角线OB与双曲线y相交于点D,且OD:OB=2:3,则k的值为( )
A.12 B.﹣12 C.16 D.﹣16
7.(2021·黑龙江·中考真题)如图,在平面直角坐标系中,菱形的边轴,垂足为,顶点在第二象限,顶点在轴正半轴上,反比例函数的图象同时经过顶点.若点的横坐标为5,,则的值为( )
A. B. C. D.
8.(2021·辽宁丹东·中考真题)如图,点A在曲线到上,点B在双曲线上,轴,点C是x轴上一点,连接、,若的面积是6,则k的值( )
A. B. C. D.
9.(2021·吉林长春·中考真题)如图,在平面直角坐标系中,点A、B在函数的图象上,x过点A作x轴的垂线,与函数的图象交于点C,连结BC交x轴于点D.若点A的横坐标为1,,则点B的横坐标为( )
A. B. C. D.
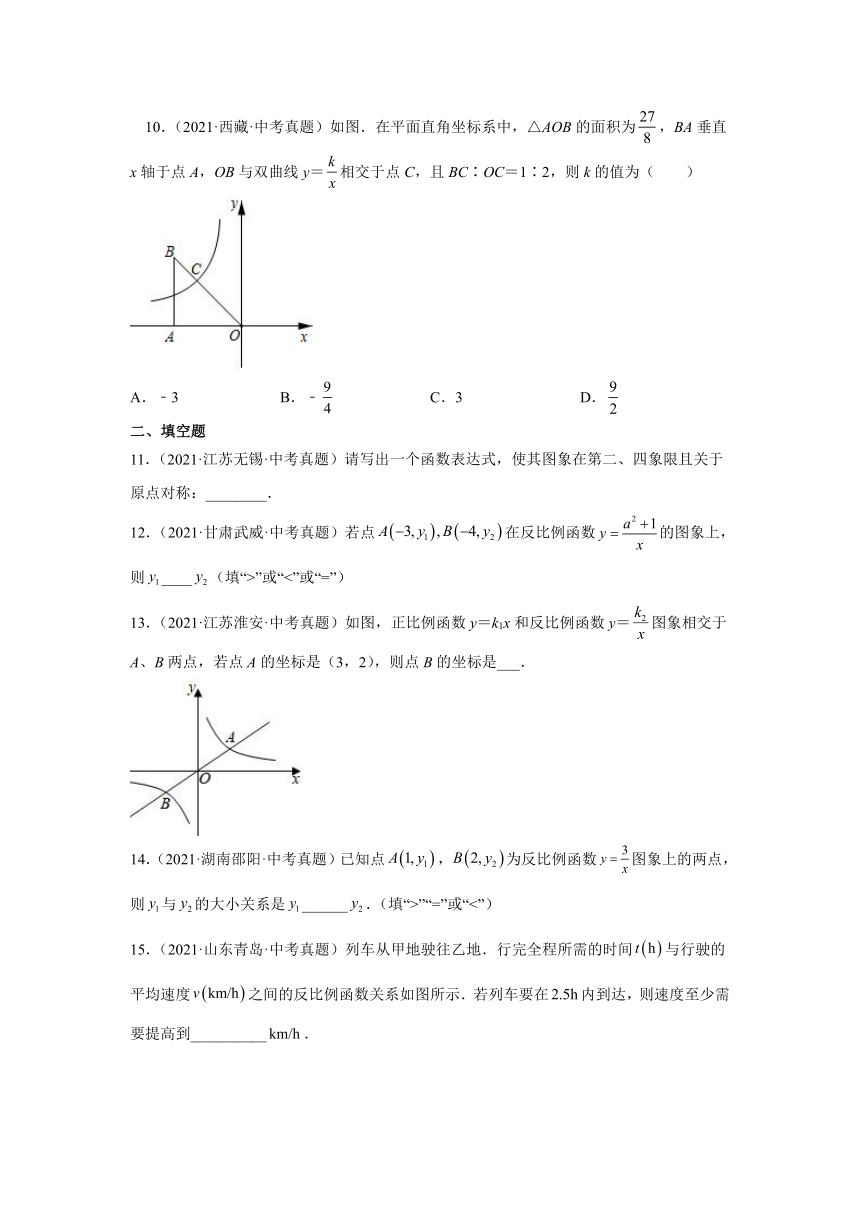
10.(2021·西藏·中考真题)如图.在平面直角坐标系中,△AOB的面积为,BA垂直x轴于点A,OB与双曲线y=相交于点C,且BC∶OC=1∶2,则k的值为( )
A.﹣3 B.﹣ C.3 D.
二、填空题
11.(2021·江苏无锡·中考真题)请写出一个函数表达式,使其图象在第二、四象限且关于原点对称:________.
12.(2021·甘肃武威·中考真题)若点在反比例函数的图象上,则____(填“>”或“<”或“=”)
13.(2021·江苏淮安·中考真题)如图,正比例函数y=k1x和反比例函数y=图象相交于A、B两点,若点A的坐标是(3,2),则点B的坐标是___.
14.(2021·湖南邵阳·中考真题)已知点,为反比例函数图象上的两点,则与的大小关系是______.(填“>”“=”或“<”)
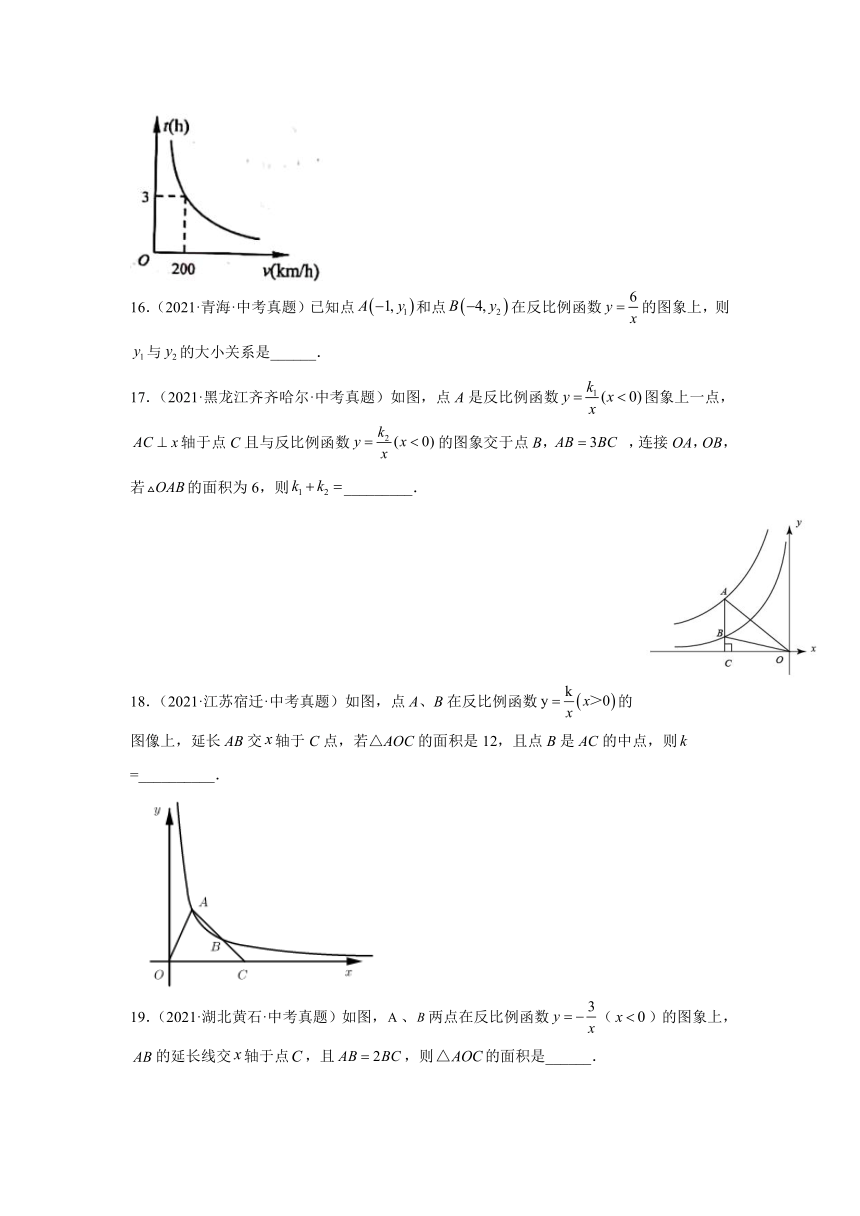
15.(2021·山东青岛·中考真题)列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到__________.
16.(2021·青海·中考真题)已知点和点在反比例函数的图象上,则与的大小关系是______.
17.(2021·黑龙江齐齐哈尔·中考真题)如图,点A是反比例函数图象上一点,轴于点C且与反比例函数的图象交于点B, ,连接OA,OB,若的面积为6,则_________.
18.(2021·江苏宿迁·中考真题)如图,点A、B在反比例函数的图像上,延长AB交轴于C点,若△AOC的面积是12,且点B是AC的中点,则 =__________.
19.(2021·湖北黄石·中考真题)如图,、两点在反比例函数()的图象上,的延长线交轴于点,且,则的面积是______.
20.(2021·广西玉林·中考真题)如图,是等腰三角形,过原点,底边轴双曲线过,两点,过点作轴交双曲线于点,若,则的值是______.
21.(2021·四川巴中·中考真题)如图,平行于y轴的直线与函数y1(x>0)和y2(x>0)的图象分别交于A、B两点,OA交双曲线y2于点C,连接CD,若OCD的面积为2,则k=_______.
22.(2021·贵州毕节·中考真题)如图,直线与反比例函数的图象交于A,B两点,与x轴交于点C,且,连接OA.已知的面积为12,则k的值为_____________.
23.(2021·辽宁锦州·中考真题)如图,在平面直角坐标系中, OABC的顶点A,B在第一象限内,顶点C在y轴上,经过点A的反比例函数y=(x>0)的图象交BC于点D.若CD=2BD, OABC的面积为15,则k的值为______.
三、解答题
24.(2021·吉林·中考真题)如图,在平面直角坐标系中,一次函数的图象与轴相交于点,与反比例函数在第一象限内的图象相交于点,过点作轴于点.
(1)求反比例函数的解析式;
(2)求的面积.
25.(2021·四川德阳·中考真题)如图,在平面直角坐标系中,反比例函数y(x>0)的图象经过点A(2,6),将点A向右平移2个单位,再向下平移a个单位得到点B,点B恰好落在反比例函数y(x>0)的图象上,过A,B两点的直线与y轴交于点C.
(1)求k的值及点C的坐标;
(2)在y轴上有一点D(0,5),连接AD,BD,求△ABD的面积.
26.(2021·四川凉山·中考真题)如图,中,,边OB在x轴上,反比例函数的图象经过斜边OA的中点M,与AB相交于点N,.
(1)求k的值;
(2)求直线MN的解析式.
27.(2021·四川内江·中考真题)如图,一次函数的图象与反比例函数的图像相交于、两点.
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出满足的的取值范围;
(3)若点在线段上,且,求点的坐标.
28.(2021·广西百色·中考真题)如图,O为坐标原点,直线l⊥y轴,垂足为M,反比例函数y=(k≠0)的图象与l交于点A(m,3),△AOM的面积为6
(1)求m、k的值;
(2)在x轴正半轴上取一点B,使OB=OA,求直线AB的函数表达式.
29.(2021·广西贵港·中考真题)如图,一次函数y=x+2的图象与反比例函数的图象相交,其中一个交点的横坐标是1.
(1)求k的值;
(2)若将一次函数y=x+2的图象向下平移4个单位长度,平移后所得到的图象与反比例函数的图象相交于A,B两点,求此时线段AB的长.
30.(2021·山东聊城·中考真题)如图,过C点的直线y=﹣x﹣2与x轴,y轴分别交于点A,B两点,且BC=AB,过点C作CH⊥x轴,垂足为点H,交反比例函数y=(x>0)的图象于点D,连接OD,△ODH的面积为6
(1)求k值和点D的坐标;
(2)如图,连接BD,OC,点E在直线y=﹣x﹣2上,且位于第二象限内,若△BDE的面积是△OCD面积的2倍,求点E的坐标.
31.(2021·四川南充·中考真题)如图,反比例函数的图象与过点,的直线交于点B和C.
(1)求直线AB和反比例函数的解析式.
(2)已知点,直线CD与反比例函数图象在第一象限的交点为E,直接写出点E的坐标,并求的面积.
参考答案
1.B 2.C 3.A 4.A 5.A 6.D 7.A 8.C 9.B 10.A
11.(答案不唯一) 12. 13.(﹣3,﹣2) 14.> 15.240 16.
17. 18.8 19. 20.3 21.8 22.8. 23.18
24.
解:(1)∵点是直线与反比例函数交点,
∴点坐标满足一次函数解析式,
∴,
∴,
∴,
∴,
∴反比例函数的解析式为;
(2)∵轴,
∴,轴,
∴,
令,则,
∴,
∴,
∴,
∴的面积为6
25.
解:(1)把点代入,,
反比例函数的解析式为,
将点向右平移2个单位,
,
当时,,
,
设直线的解析式为,
由题意可得,
解得,
,
当时,,
;
(2)由(1)知,
.
26.
解:(1)设点A坐标为(m,n),
∵∠ABO=90°,
∴B(m,0),又AN=,
∴N(m,),
∵△AOB的面积为12,
∴,即,
∵M为OA中点,
∴M(,),
∵M和N在反比例函数图像上,
∴,化简可得:,又,
∴,解得:,
∴,
∴M(2,3),代入,
得;
(2)由(1)可得:M(2,3),N(4,),
设直线MN的表达式为y=ax+b,
则,解得:,
∴直线MN的表达式为.
27.
解:(1)反比例函数经过,
,
反比例函数为,
在比例函数的图象上,
,
,
直线经过,,
,解得,
一次函数的解析式为;
(2)观察图象,的的取值范围是或;
(3)设,
,
,
即,
,
解得,(舍去),
点坐标为(,).
28.
解:(1)∵直线l⊥y轴,垂足为M
∴AM⊥OM
∴
∵A点的坐标为(m,3)
∴,
∴
解得
∴A点的坐标为(4,3)
∵A点在反比例函数上
∴
解得;
(2) 设直线AB的解析式为
由(1)得A点的坐标为(4,3)
即,
∴
∵B在x正半轴上,且OB=OA
∴OB=5,即B的坐标为(5,0)
∴
解得
∴直线AB的解析式为.
29.
解:(1)将代入,
交点的坐标为,
将代入,
解得:;
(2)将一次函数的图象向下平移4个单位长度得到,
由,
解得:或,
,,
.
30.
解∶(1)设点 D 坐标为(m,n),
由题意得.
∵点 D在的图象上,.
∵直线的图象与轴交于点A,
∴点A 的坐标为(-4,0).
∵CHx轴,CH//y 轴..
点D在反比例函数的图象上,
点 D 坐标为(4,3)
(2)由(1)知轴,.
.
过点E作EFCD,垂足为点 F,交y轴于点M,
.
.
∴点 E 的横坐标为-8.
∵点E 在直线上,∴点E的坐标为(-8,2).
31.
(1)设直线AB的解析式为,
将点,代入解析式得:
,解得:,
∴直线AB的解析式为:;
设反比例函数解析式为:,
将代入解析式得:,
∴反比例函数的解析式为:;
(2)联立,解得:或,
∴C点坐标为:,
设直线CD的解析式为:,
将,代入得:
,解得:,
∴直线CD的解析式为:,
联立,解得:或,
∴E点的坐标为:;
如图,过E点作EF∥y轴,交直线AB于F点,
则F点坐标为,,
∴.
姓名:___________班级:___________
一、单选题
1.(2021·黑龙江大庆·中考真题)已知反比例函数,当时,随的增大而减小,那么一次的数的图像经过第( )
A.一,二,三象限 B.一,二,四象限
C.一,三,四象限 D.二,三,四象限
2.(2021·贵州安顺·中考真题)已知反比例函数的图象与正比例函数的图象相交于两点,若点的坐标是,则点的坐标是( )
A. B. C. D.
3.(2021·辽宁朝阳·中考真题)如图,O是坐标原点,点B在x轴上,在OAB中,AO=AB=5,OB=6,点A在反比例函数y=(k≠0)图象上,则k的值( )
A.﹣12 B.﹣15 C.﹣20 D.﹣30
4.(2021·江苏宿迁·中考真题)已知双曲线过点(3,)、(1,)、(-2,),则下列结论正确的是( )
A. B. C. D.
5.(2021·辽宁大连·中考真题)下列说法正确的是( )
①反比例函数中自变量x的取值范围是;
②点在反比例函数的图象上;
③反比例函数的图象,在每一个象限内,y随x的增大而增大.
A.①② B.①③ C.②③ D.①②③
6.(2021·黑龙江牡丹江·中考真题)如图,矩形OABC的面积为36,它的对角线OB与双曲线y相交于点D,且OD:OB=2:3,则k的值为( )
A.12 B.﹣12 C.16 D.﹣16
7.(2021·黑龙江·中考真题)如图,在平面直角坐标系中,菱形的边轴,垂足为,顶点在第二象限,顶点在轴正半轴上,反比例函数的图象同时经过顶点.若点的横坐标为5,,则的值为( )
A. B. C. D.
8.(2021·辽宁丹东·中考真题)如图,点A在曲线到上,点B在双曲线上,轴,点C是x轴上一点,连接、,若的面积是6,则k的值( )
A. B. C. D.
9.(2021·吉林长春·中考真题)如图,在平面直角坐标系中,点A、B在函数的图象上,x过点A作x轴的垂线,与函数的图象交于点C,连结BC交x轴于点D.若点A的横坐标为1,,则点B的横坐标为( )
A. B. C. D.
10.(2021·西藏·中考真题)如图.在平面直角坐标系中,△AOB的面积为,BA垂直x轴于点A,OB与双曲线y=相交于点C,且BC∶OC=1∶2,则k的值为( )
A.﹣3 B.﹣ C.3 D.
二、填空题
11.(2021·江苏无锡·中考真题)请写出一个函数表达式,使其图象在第二、四象限且关于原点对称:________.
12.(2021·甘肃武威·中考真题)若点在反比例函数的图象上,则____(填“>”或“<”或“=”)
13.(2021·江苏淮安·中考真题)如图,正比例函数y=k1x和反比例函数y=图象相交于A、B两点,若点A的坐标是(3,2),则点B的坐标是___.
14.(2021·湖南邵阳·中考真题)已知点,为反比例函数图象上的两点,则与的大小关系是______.(填“>”“=”或“<”)
15.(2021·山东青岛·中考真题)列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到__________.
16.(2021·青海·中考真题)已知点和点在反比例函数的图象上,则与的大小关系是______.
17.(2021·黑龙江齐齐哈尔·中考真题)如图,点A是反比例函数图象上一点,轴于点C且与反比例函数的图象交于点B, ,连接OA,OB,若的面积为6,则_________.
18.(2021·江苏宿迁·中考真题)如图,点A、B在反比例函数的图像上,延长AB交轴于C点,若△AOC的面积是12,且点B是AC的中点,则 =__________.
19.(2021·湖北黄石·中考真题)如图,、两点在反比例函数()的图象上,的延长线交轴于点,且,则的面积是______.
20.(2021·广西玉林·中考真题)如图,是等腰三角形,过原点,底边轴双曲线过,两点,过点作轴交双曲线于点,若,则的值是______.
21.(2021·四川巴中·中考真题)如图,平行于y轴的直线与函数y1(x>0)和y2(x>0)的图象分别交于A、B两点,OA交双曲线y2于点C,连接CD,若OCD的面积为2,则k=_______.
22.(2021·贵州毕节·中考真题)如图,直线与反比例函数的图象交于A,B两点,与x轴交于点C,且,连接OA.已知的面积为12,则k的值为_____________.
23.(2021·辽宁锦州·中考真题)如图,在平面直角坐标系中, OABC的顶点A,B在第一象限内,顶点C在y轴上,经过点A的反比例函数y=(x>0)的图象交BC于点D.若CD=2BD, OABC的面积为15,则k的值为______.
三、解答题
24.(2021·吉林·中考真题)如图,在平面直角坐标系中,一次函数的图象与轴相交于点,与反比例函数在第一象限内的图象相交于点,过点作轴于点.
(1)求反比例函数的解析式;
(2)求的面积.
25.(2021·四川德阳·中考真题)如图,在平面直角坐标系中,反比例函数y(x>0)的图象经过点A(2,6),将点A向右平移2个单位,再向下平移a个单位得到点B,点B恰好落在反比例函数y(x>0)的图象上,过A,B两点的直线与y轴交于点C.
(1)求k的值及点C的坐标;
(2)在y轴上有一点D(0,5),连接AD,BD,求△ABD的面积.
26.(2021·四川凉山·中考真题)如图,中,,边OB在x轴上,反比例函数的图象经过斜边OA的中点M,与AB相交于点N,.
(1)求k的值;
(2)求直线MN的解析式.
27.(2021·四川内江·中考真题)如图,一次函数的图象与反比例函数的图像相交于、两点.
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出满足的的取值范围;
(3)若点在线段上,且,求点的坐标.
28.(2021·广西百色·中考真题)如图,O为坐标原点,直线l⊥y轴,垂足为M,反比例函数y=(k≠0)的图象与l交于点A(m,3),△AOM的面积为6
(1)求m、k的值;
(2)在x轴正半轴上取一点B,使OB=OA,求直线AB的函数表达式.
29.(2021·广西贵港·中考真题)如图,一次函数y=x+2的图象与反比例函数的图象相交,其中一个交点的横坐标是1.
(1)求k的值;
(2)若将一次函数y=x+2的图象向下平移4个单位长度,平移后所得到的图象与反比例函数的图象相交于A,B两点,求此时线段AB的长.
30.(2021·山东聊城·中考真题)如图,过C点的直线y=﹣x﹣2与x轴,y轴分别交于点A,B两点,且BC=AB,过点C作CH⊥x轴,垂足为点H,交反比例函数y=(x>0)的图象于点D,连接OD,△ODH的面积为6
(1)求k值和点D的坐标;
(2)如图,连接BD,OC,点E在直线y=﹣x﹣2上,且位于第二象限内,若△BDE的面积是△OCD面积的2倍,求点E的坐标.
31.(2021·四川南充·中考真题)如图,反比例函数的图象与过点,的直线交于点B和C.
(1)求直线AB和反比例函数的解析式.
(2)已知点,直线CD与反比例函数图象在第一象限的交点为E,直接写出点E的坐标,并求的面积.
参考答案
1.B 2.C 3.A 4.A 5.A 6.D 7.A 8.C 9.B 10.A
11.(答案不唯一) 12. 13.(﹣3,﹣2) 14.> 15.240 16.
17. 18.8 19. 20.3 21.8 22.8. 23.18
24.
解:(1)∵点是直线与反比例函数交点,
∴点坐标满足一次函数解析式,
∴,
∴,
∴,
∴,
∴反比例函数的解析式为;
(2)∵轴,
∴,轴,
∴,
令,则,
∴,
∴,
∴,
∴的面积为6
25.
解:(1)把点代入,,
反比例函数的解析式为,
将点向右平移2个单位,
,
当时,,
,
设直线的解析式为,
由题意可得,
解得,
,
当时,,
;
(2)由(1)知,
.
26.
解:(1)设点A坐标为(m,n),
∵∠ABO=90°,
∴B(m,0),又AN=,
∴N(m,),
∵△AOB的面积为12,
∴,即,
∵M为OA中点,
∴M(,),
∵M和N在反比例函数图像上,
∴,化简可得:,又,
∴,解得:,
∴,
∴M(2,3),代入,
得;
(2)由(1)可得:M(2,3),N(4,),
设直线MN的表达式为y=ax+b,
则,解得:,
∴直线MN的表达式为.
27.
解:(1)反比例函数经过,
,
反比例函数为,
在比例函数的图象上,
,
,
直线经过,,
,解得,
一次函数的解析式为;
(2)观察图象,的的取值范围是或;
(3)设,
,
,
即,
,
解得,(舍去),
点坐标为(,).
28.
解:(1)∵直线l⊥y轴,垂足为M
∴AM⊥OM
∴
∵A点的坐标为(m,3)
∴,
∴
解得
∴A点的坐标为(4,3)
∵A点在反比例函数上
∴
解得;
(2) 设直线AB的解析式为
由(1)得A点的坐标为(4,3)
即,
∴
∵B在x正半轴上,且OB=OA
∴OB=5,即B的坐标为(5,0)
∴
解得
∴直线AB的解析式为.
29.
解:(1)将代入,
交点的坐标为,
将代入,
解得:;
(2)将一次函数的图象向下平移4个单位长度得到,
由,
解得:或,
,,
.
30.
解∶(1)设点 D 坐标为(m,n),
由题意得.
∵点 D在的图象上,.
∵直线的图象与轴交于点A,
∴点A 的坐标为(-4,0).
∵CHx轴,CH//y 轴..
点D在反比例函数的图象上,
点 D 坐标为(4,3)
(2)由(1)知轴,.
.
过点E作EFCD,垂足为点 F,交y轴于点M,
.
.
∴点 E 的横坐标为-8.
∵点E 在直线上,∴点E的坐标为(-8,2).
31.
(1)设直线AB的解析式为,
将点,代入解析式得:
,解得:,
∴直线AB的解析式为:;
设反比例函数解析式为:,
将代入解析式得:,
∴反比例函数的解析式为:;
(2)联立,解得:或,
∴C点坐标为:,
设直线CD的解析式为:,
将,代入得:
,解得:,
∴直线CD的解析式为:,
联立,解得:或,
∴E点的坐标为:;
如图,过E点作EF∥y轴,交直线AB于F点,
则F点坐标为,,
∴.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
