人教版数学七年级下册 9.2-实际问题与一元一次不等式课件(共25张PPT)
文档属性
| 名称 | 人教版数学七年级下册 9.2-实际问题与一元一次不等式课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-10 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
到哪家商场购物更实惠?
甲、乙两商场以 价格出售 的商品,并且又各自推出不同的优惠方案:
顾客怎样选择商场购物能获得更大优惠?
同样
同样
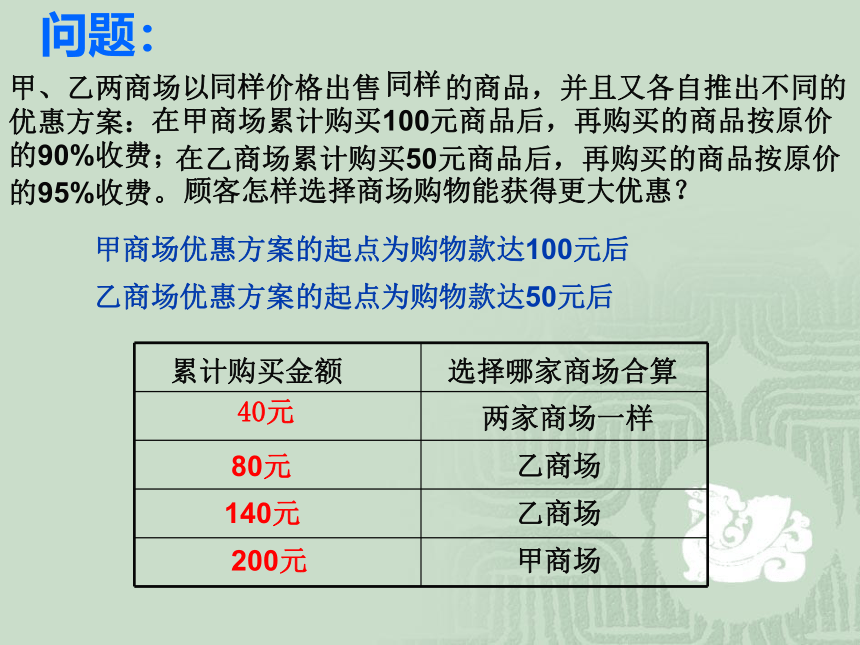
在甲商场累计购买100元商品后,再购买的商品按原价的90%收费;
在乙商场累计购买50元商品后,再购买的商品按原价的95%收费。
甲商场优惠方案的起点为购物款达100元后
乙商场优惠方案的起点为购物款达50元后
40元
累计购买金额
选择哪家商场合算
两家商场一样
乙商场
140元
200元
80元
甲商场
乙商场
问题:
3、如果累计购物超过100元;
(1)什么情况下,在甲商场花费小?
(2)什么情况下,在乙商场花费小?
(3)什么情况下,在两家商场购物花费一样?
在乙商场花费小。
又有三种情况:
甲、乙两商场以同样价格出售同样的商品。并且又各自推出不同的优惠方案:在甲商场累计购买100元商品后,再购买的商品按原价的90%收费;在乙商场累计购买50元商品后,再购买的商品按原价的95%收费。顾客怎样选择商场购物能获得更大优惠?
分三种情况分析:
设累计购物x元(x>100元)。
则在甲商场的花费为
在乙商场的花费为
(1)如果在甲商场花费小,则
1、如果累计购物不超过50元;
在两家商场购物花费时一样的。
2、如果累计购物超过50元但不超过100元时;
设累计购物x元(x>100元)。
则在甲商场的花费为
在甲商场的花费为
(1)如果在甲商场花费小,则
去括号,得:
移项,得:
合并,得:
系数化为1,得:
这就是说,累计购物超过150元时在甲商场购物花费小。
(2)累计购物超过100元但小于150元时,
(3)累计购物刚好是150元时,
在乙商场购物花费小.
在两家商场购物花费一样多.
某单位计划10月份组织员工到杭州旅游,人数估计 在10到25人之间,甲、乙两旅行社的服务质量相同且组织到杭州旅游的价格都是每人200元,该单位联系时,甲旅行社表示可以给予每位游客七五折优惠,乙旅行社表示可以免去一带队领导的旅游费用,其余游客八折优惠。问该单位怎样选择,可使支付的旅游总费用较少?
解:设该单位去x人,则:
支付甲旅行社0.75× 200x=150x
支付乙旅行社0.8 × 200(x-1)=160x-160 讨论:
(1)当支付甲旅行社和乙旅行社费用相同时:
150x=160x-160 解得:x =16
(2)当支付甲旅行社大于乙旅行社费用时:
150x>160x-160 解得:x<16
(3)当支付甲旅行社小于乙旅行社费用时:
150x < 160x-160
解得:x>16
一、填空题:
1、某校七年级一班共有60人,期中考试数学及格人数为x人,符合学校要求的及格率不低于87%的要求,用不等式表示x应满足的条件为( )。
2、甲、乙两地相距26千米,某人要在6.5小时内从甲地走到乙地,设这人每小时至少走x千米,用不等式表示题目中的关系为( )。
3、开学前,小红拿了10元钱到文具店买笔记本和作文本,作文本每本8角,她买了6本,笔记本每本6角,她最多还能买( )本。
二、生活在线
1、一组学生到校门口拍一张合影,已知冲一张底片需要0.6元,洗一张照片需要0.4元,每人都要得到一张照片,每人分担的钱不能超过0.5元。那么参加合影的同学至少有几人?
解:设参加合影的人数有x人。
0.6+0.4x≤0.5x
解得:x≥6
答:参加合影的至少有6人。
2、某人问一位老师,他所教的班有多少名学生,老师说:“一半的学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩不足6位同学在操场上踢足球”。求这个班共有多少名学生?
解:设这个班有学生x名。根据题意,得:
解得:x<56
是正整数
∴ x是2、4、7的最小公倍数
∴ x=28
由题意知2002年北京天气良好的天数是
设2008年增加的良好天数是x天,则2008年的良好天数 是 天
解:设2008年比2002年增加的良好天数是x天,根据题意得
解此不等式得:x>55.45
由x应为整数,得x≥56
365×55%
x+365×55%
解:设小明答对x道题,则答错或不答的题数为 20-x ,根据他的得分要超过90,得
10x-5(20-x)>90
解此不等式得:x>
在本题中,x 应是 数而且不能少于 ,所以小明至少要答对 道题。
整
13
例1:某次“人与自然”知识竞赛是共有20道题,做一道题,对一题得10分,答错一道或不答扣5分则至少答对几道题其得分不少于是80分?
解:
设答对的题数为X,则答错的不等式为20-X.
根据题意得:
10X-5(20-X)≥ 80
解不等式得 X ≥ 12
答:至少要答对12道题,其得分不少于80分。
思考:本题问他答对了多少道题,又怎么做?
90<10x-5(20-x)≤20×10
解得: <x≤20
故答对13或14或15或16或17或18或19或20
3、某市自来水公司按如下标准收费:用户每月用水在5立方米之内的,按每立方米1.5元收费;超出5立方米的部分,每立方米收费2元。小明家某月的水费超过了15元,那么他家这个月的用水量至少是多少?(取整数)
解:设小明家这个月的用水量为x立方米。
1.5 ×5+2(x-5)>15
解得:x >8.75
因为x取整数
所以x ≥ 9
答:小明家这个月的用水量至少为9立方米。
为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,A型设备的价格是每台12万元,B型设备的价格是每台10万元。经预算,该企业购买设备的资金不高于105万元。请你设计该企业有几种购买方案。
变式:若企业每月生产的污水量为2040吨,A型设备每月可处理污水240吨,B型机每月处理污水200吨,为了节约资金,应选择哪种方案?
解:(1)设购买污水处理设备A型x台,则B型为(10-x)台,依题意得:
去括号,得:
因为x取非负整数,所以
所以有三种购买方案:A型0台,B型10台;A型1台,B型9台;A型2台,B型8台。
移项且合并得:
系数化为1,得:
(2)由题意得:
去括号,得:
所以x为1或2。当x=1时,购买资金为
万元;当x=2时,购买资金为
万元。因此,为节约资金,应选购A型1台,B型9台。
移项且合并得:
系数化为1,得:
变式:若企业每月生产的污水量为2040吨,A型设备每月可处理污水240吨,B型机每月处理污水200吨,为了节约资金,应选择哪种方案?
通过体验选商场购物、旅游、洗照片等实际问题,感受实际生活中存在不等关系,用不等式来表示这种关系为解决问题带来方便。由实际问题中的不等关系列出不等式,就把实际问题转化为数学问题,再通过解不等式可得到实际问题的答案。
课本:141页 7、8、9。
到哪家商场购物更实惠?
甲、乙两商场以 价格出售 的商品,并且又各自推出不同的优惠方案:
顾客怎样选择商场购物能获得更大优惠?
同样
同样
在甲商场累计购买100元商品后,再购买的商品按原价的90%收费;
在乙商场累计购买50元商品后,再购买的商品按原价的95%收费。
甲商场优惠方案的起点为购物款达100元后
乙商场优惠方案的起点为购物款达50元后
40元
累计购买金额
选择哪家商场合算
两家商场一样
乙商场
140元
200元
80元
甲商场
乙商场
问题:
3、如果累计购物超过100元;
(1)什么情况下,在甲商场花费小?
(2)什么情况下,在乙商场花费小?
(3)什么情况下,在两家商场购物花费一样?
在乙商场花费小。
又有三种情况:
甲、乙两商场以同样价格出售同样的商品。并且又各自推出不同的优惠方案:在甲商场累计购买100元商品后,再购买的商品按原价的90%收费;在乙商场累计购买50元商品后,再购买的商品按原价的95%收费。顾客怎样选择商场购物能获得更大优惠?
分三种情况分析:
设累计购物x元(x>100元)。
则在甲商场的花费为
在乙商场的花费为
(1)如果在甲商场花费小,则
1、如果累计购物不超过50元;
在两家商场购物花费时一样的。
2、如果累计购物超过50元但不超过100元时;
设累计购物x元(x>100元)。
则在甲商场的花费为
在甲商场的花费为
(1)如果在甲商场花费小,则
去括号,得:
移项,得:
合并,得:
系数化为1,得:
这就是说,累计购物超过150元时在甲商场购物花费小。
(2)累计购物超过100元但小于150元时,
(3)累计购物刚好是150元时,
在乙商场购物花费小.
在两家商场购物花费一样多.
某单位计划10月份组织员工到杭州旅游,人数估计 在10到25人之间,甲、乙两旅行社的服务质量相同且组织到杭州旅游的价格都是每人200元,该单位联系时,甲旅行社表示可以给予每位游客七五折优惠,乙旅行社表示可以免去一带队领导的旅游费用,其余游客八折优惠。问该单位怎样选择,可使支付的旅游总费用较少?
解:设该单位去x人,则:
支付甲旅行社0.75× 200x=150x
支付乙旅行社0.8 × 200(x-1)=160x-160 讨论:
(1)当支付甲旅行社和乙旅行社费用相同时:
150x=160x-160 解得:x =16
(2)当支付甲旅行社大于乙旅行社费用时:
150x>160x-160 解得:x<16
(3)当支付甲旅行社小于乙旅行社费用时:
150x < 160x-160
解得:x>16
一、填空题:
1、某校七年级一班共有60人,期中考试数学及格人数为x人,符合学校要求的及格率不低于87%的要求,用不等式表示x应满足的条件为( )。
2、甲、乙两地相距26千米,某人要在6.5小时内从甲地走到乙地,设这人每小时至少走x千米,用不等式表示题目中的关系为( )。
3、开学前,小红拿了10元钱到文具店买笔记本和作文本,作文本每本8角,她买了6本,笔记本每本6角,她最多还能买( )本。
二、生活在线
1、一组学生到校门口拍一张合影,已知冲一张底片需要0.6元,洗一张照片需要0.4元,每人都要得到一张照片,每人分担的钱不能超过0.5元。那么参加合影的同学至少有几人?
解:设参加合影的人数有x人。
0.6+0.4x≤0.5x
解得:x≥6
答:参加合影的至少有6人。
2、某人问一位老师,他所教的班有多少名学生,老师说:“一半的学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩不足6位同学在操场上踢足球”。求这个班共有多少名学生?
解:设这个班有学生x名。根据题意,得:
解得:x<56
是正整数
∴ x是2、4、7的最小公倍数
∴ x=28
由题意知2002年北京天气良好的天数是
设2008年增加的良好天数是x天,则2008年的良好天数 是 天
解:设2008年比2002年增加的良好天数是x天,根据题意得
解此不等式得:x>55.45
由x应为整数,得x≥56
365×55%
x+365×55%
解:设小明答对x道题,则答错或不答的题数为 20-x ,根据他的得分要超过90,得
10x-5(20-x)>90
解此不等式得:x>
在本题中,x 应是 数而且不能少于 ,所以小明至少要答对 道题。
整
13
例1:某次“人与自然”知识竞赛是共有20道题,做一道题,对一题得10分,答错一道或不答扣5分则至少答对几道题其得分不少于是80分?
解:
设答对的题数为X,则答错的不等式为20-X.
根据题意得:
10X-5(20-X)≥ 80
解不等式得 X ≥ 12
答:至少要答对12道题,其得分不少于80分。
思考:本题问他答对了多少道题,又怎么做?
90<10x-5(20-x)≤20×10
解得: <x≤20
故答对13或14或15或16或17或18或19或20
3、某市自来水公司按如下标准收费:用户每月用水在5立方米之内的,按每立方米1.5元收费;超出5立方米的部分,每立方米收费2元。小明家某月的水费超过了15元,那么他家这个月的用水量至少是多少?(取整数)
解:设小明家这个月的用水量为x立方米。
1.5 ×5+2(x-5)>15
解得:x >8.75
因为x取整数
所以x ≥ 9
答:小明家这个月的用水量至少为9立方米。
为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,A型设备的价格是每台12万元,B型设备的价格是每台10万元。经预算,该企业购买设备的资金不高于105万元。请你设计该企业有几种购买方案。
变式:若企业每月生产的污水量为2040吨,A型设备每月可处理污水240吨,B型机每月处理污水200吨,为了节约资金,应选择哪种方案?
解:(1)设购买污水处理设备A型x台,则B型为(10-x)台,依题意得:
去括号,得:
因为x取非负整数,所以
所以有三种购买方案:A型0台,B型10台;A型1台,B型9台;A型2台,B型8台。
移项且合并得:
系数化为1,得:
(2)由题意得:
去括号,得:
所以x为1或2。当x=1时,购买资金为
万元;当x=2时,购买资金为
万元。因此,为节约资金,应选购A型1台,B型9台。
移项且合并得:
系数化为1,得:
变式:若企业每月生产的污水量为2040吨,A型设备每月可处理污水240吨,B型机每月处理污水200吨,为了节约资金,应选择哪种方案?
通过体验选商场购物、旅游、洗照片等实际问题,感受实际生活中存在不等关系,用不等式来表示这种关系为解决问题带来方便。由实际问题中的不等关系列出不等式,就把实际问题转化为数学问题,再通过解不等式可得到实际问题的答案。
课本:141页 7、8、9。
